
- •Лабораторная работа № 5 Планарность и раскраска
- •Теоретическая справка Плоские и планарные графы. Планарность
- •Теорема Жордана.
- •Теорема Эйлера для плоского графа.
- •Критерии планарности
- •Алгоритм плоской укладки графа
- •Алгоритм .
- •Характеристики не планарных графов
- •Раскраска графов
- •Теорема Кёнига Непустой граф является бихроматическим тогда и только тогда, когда он не содержит циклов нечетной длины.
- •Алгоритм последовательной раскраски
- •Раскраска ребер
- •Задание к лабораторной работе
Алгоритм .
Выберем некоторый простой цикл CграфаGи уложим его на плоскости (лучше выбирать окружение).
Найдем грани графа
 и множество сегментовSотносительно
и множество сегментовSотносительно
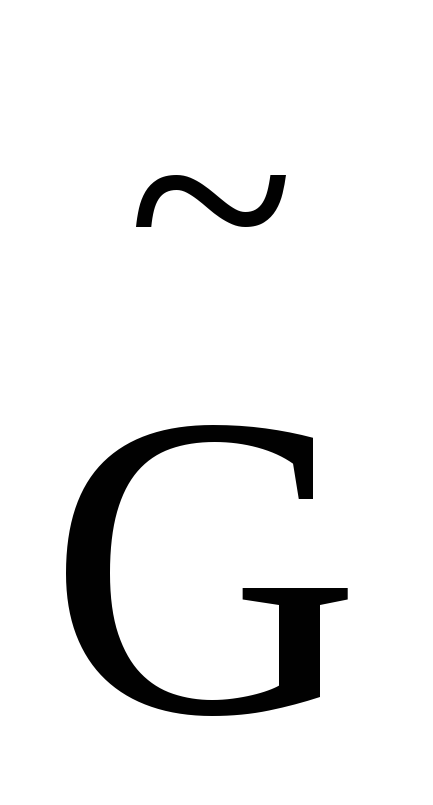 .
Если множество сегментов пусто перейти
к п. 7.
.
Если множество сегментов пусто перейти
к п. 7.Для каждого сегмента Sнайдем множество допустимых граней Г (S).
Если существует сегмент Sдля которого Г (S) =(множество граней пусто), то граф G не планарен. Выход из алгоритма, иначе переход к п. 4.
Если существует сегмент Sдля которого ровно одна допустимая грань (|Г(S)| = 1), то перейдем к п. 6, иначе п. 5.
Для некоторого сегмента Sвыбираем произвольную допустимую грань Г.
Поместим произвольную -цепь L, принадлежащую S, в грань Г, заменим
 на
на L и перейдем к п. 1.
L и перейдем к п. 1.Построена
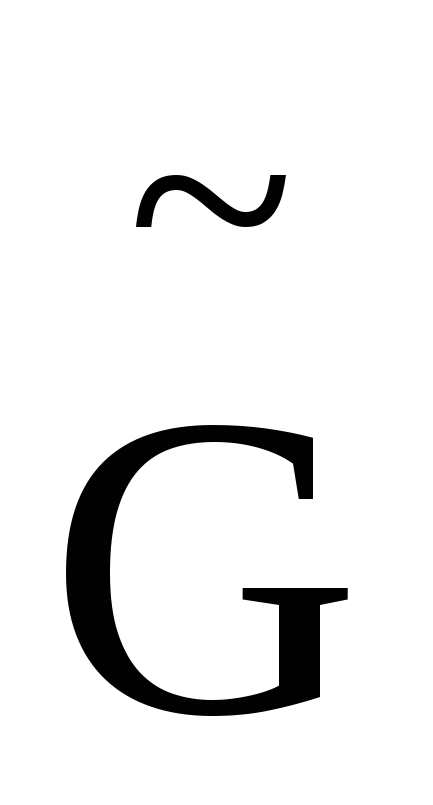 плоская укладка графаG.
Шагом алгоритма считается присоединение
к
плоская укладка графаG.
Шагом алгоритма считается присоединение
к
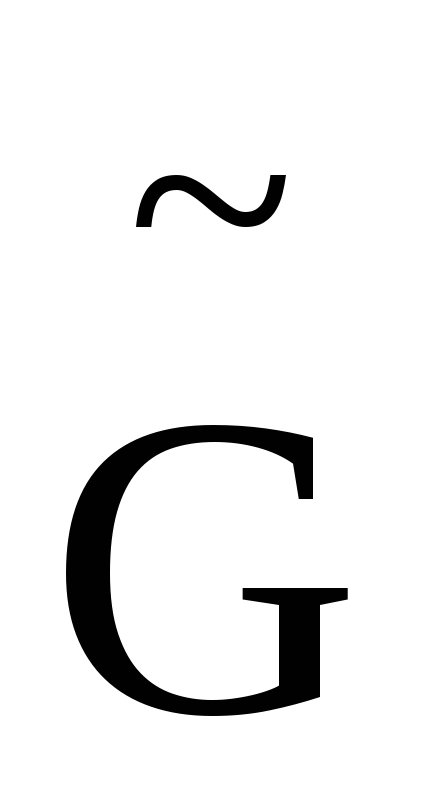 опр.-цепи.
опр.-цепи.
Пример:
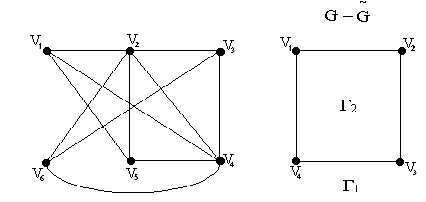
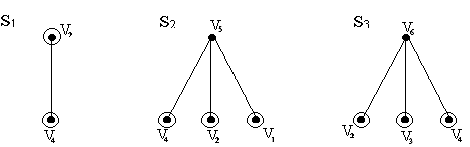
Г(S1) = Г(S2) = Г(S3) = {Г1, Г2}
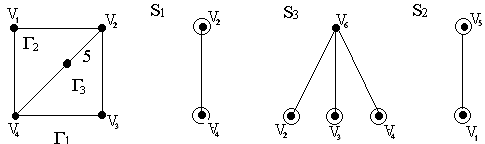
S2:-цепь = {4, 5, 2} в Г2
Г(S1) = {Г1, Г2, Г3}, Г(S2) = {Г2}, Г(S3) = {Г1, Г3}
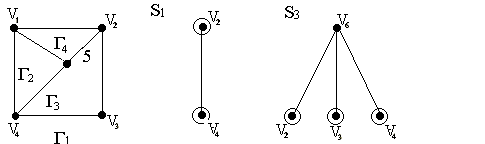
S2:-цепь = {1, 5,} в Г2
Г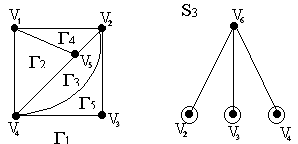 (S1)
= {Г1, Г3},
Г(S3)
= {Г1, Г3}
(S1)
= {Г1, Г3},
Г(S3)
= {Г1, Г3}
S1:-цепь = {2, 4,} в Г3
Г (S3)
= {Г1, Г5}
(S3)
= {Г1, Г5}

S3:цепь: {2, 6, 3} в Г1
Г(S) = {Г1}
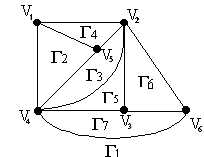
S: -цепь = {4, 6} в Г1
Характеристики не планарных графов
Число скрещиванийграфаGэтоminчисло пересечений
двух ребер при изображении графаGна плоскости (обозначают![]() (G)).
Число скрещиваний равно 0, если граф
планарен.
(G)).
Число скрещиваний равно 0, если граф
планарен.
Искаженность Gэто минимальное число ребер, удаление которых приводит к планарному графу (обозначают sk(G)).
ТолщинаGэто минимальное число его планарных подграфов, объединение которых дает исходный граф G (обозначают t(G)).
Род графаGэто минимальное число ручек, которые необходимо добавить к сфере, чтобы можно было уложить графGбез пересечений, самопересечений ребер.
Граф 3,3укладывается на торе без пересечений и самопересечений ребер. Такие графы называютсятороидальными, род равен 1, относятся графыK5,K7,K3, 3,K4, 4.
П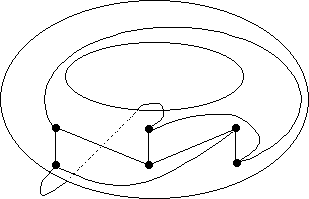 ример
укладывания графаK3,
3на торе:
ример
укладывания графаK3,
3на торе:
Раскраска графов
Пусть имеется некоторый граф Gнеор. и пустьkнатуральное число. Тогдаk-раскраскойграфаGназывается произвольная функцияf, отображающая множество вершин графаGв некотороеk-элементное множество:
f : VG {a1, a2, …, ak} = A
В качестве элементов множества Aчаще всего используется отрезок натурального ряда {1, 2, …,k} либо {a,b, …,n} или краски типа {синий, красный, …, черный}.
Раскраска называется правильной, еслиf(u)f(v) для любых смежных вершинuиvграфаG(или концевые вершины любого ребра окрашены в разные цвета).
Граф, для которого существует правильная k-раскраска, называетсяk-раскрашиваемым.
П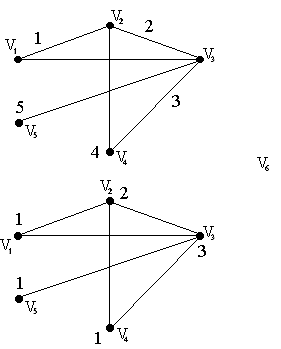 ример:
ример:
граф 5-раскрашиваемый
(раскраска правильная)
правильная раскраска
граф 3-раскрашиваемый
Хроматическое число графа G это минимальное число красок, при котором граф имеет правильную раскраску. Если хроматическое число равноk, то граф называетсяk-хроматическим. (обозначают(G) =k).
Правильную k-раскраскуграфаGможно рассматривать как разбиение множества вершин графаGна не более чем,kнепустых множеств, которые называютсяцветными классами.
V=V1 …Vk
Каждый цветной класс является независимым множеством, т. е. разбиение множества вершин (эквивалентны, транзитивность не является сюрьективной).
Для полного графа Knхроматическое число равно:
(Kn) =n,
для цикла с четным числом вершин: (Cчетн.) = 2
С нечетным числом вершин:
(C2n + 1) = 3
Для пустого: (0n) = 1
Граф, у которого = 2 называютсябихроматическим.
