Конечные автоматы

Детерминированным конечным автоматом называется произвольная пятерка следующего вида: M ={Q, , δ, S ,F}

При этом:

Q, , F – конечные множества

SQ, FQ, δ:Q→Q

δ – функция перехода из Q →Q

– алфавит автомата М (входной)

Q – множество состояний конечного автомата (внутренний алфавит)

S – начальное состояние

F – множество конечных состояний

δ_iq₁q₂Q и a q₂ = δ(q₁,a)

Если q₁q₂Q и для некоторых a можно записать q₂ = δ(q₁,a), то говорят что автомат М переходит из состояния q₁ в состояние q₂ под действием а.

Конечные автоматы изображаются графами(рис.3): вершины – состояния, дуги – переход из 1 состояния в другое при этом над дугой пишут символы, под влиянием которых осуществляется переход.

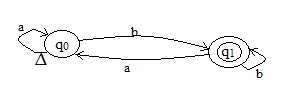
Рисунок 3 – Изображение конечного автомата.

∆ - начальное состояние

- конечное состояние

= {a,b}

Q = {q₀, q₁}

S = q₀

F = {q₁}

Q	a	b
q0	q0	q1
q1	q0	q1

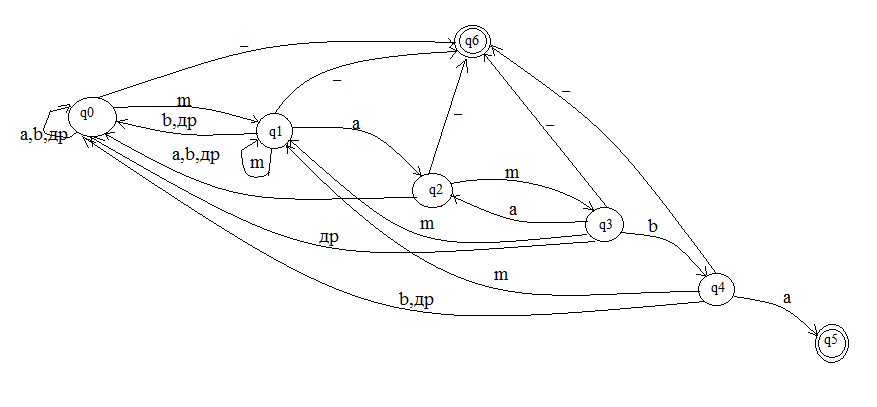
Пример: является ли слово mamba подсловом некоторого алфавита.

= {m,a,b,_,др}

Q = {q₀, q₁, q₂, q₃, q₄, q₅, q₆}

S = q₀

F = {q₅, q₆}

Q	a	b	m	_	др
q0	q0	q0	q1	q6	q0
q1	q2	q0	q1	q6	q0
q2	q0	q0	q3	q6	q0
q3	q2	q4	q1	q6	q0
q4	q5	q0	q1	q6	q0

Кодирование входного алфавита и состояний

	С
a	000
B	001
m	011
_	010
др	110

Q	С
q0	000
q1	001
q2	011
q3	010
q4	110
q5	111
q6	101

Реализация конечного автомата

∑			Q^t				Q^(t+1)
X0	X1	X2		R0	R1	R2	R0	R1	R2
0	0	0		0	0	0	0	0	0
0	0	1		0	0	0	0	0	0
0	1	1		0	0	0	0	0	1
0	1	0		0	0	0	1	0	1
1	1	0		0	0	0	0	0	0
0	0	0		0	0	1	0	1	1
0	0	1		0	0	1	0	0	0
0	1	1		0	0	1	0	0	1
0	1	0		0	0	1	1	0	1
1	1	0		0	0	1	0	0	0
0	0	0		0	1	1	0	0	0
0	0	1		0	1	1	0	0	0
0	1	1		0	1	1	0	1	0
0	1	0		0	1	1	1	0	1
1	1	0		0	1	1	0	0	0
0	0	0		0	1	0	0	1	1
0	0	1		0	1	0	1	1	0
0	1	1		0	1	0	0	0	1
0	1	0		0	1	0	1	0	1
1	1	0		0	1	0	0	0	0
0	0	0		1	1	0	1	1	1
0	0	1		1	1	0	0	0	0
0	1	1		1	1	0	0	0	1
0	1	0		1	1	0	1	0	1
1	1	0		1	1	0	0	0	0

Составим функцию для r0:

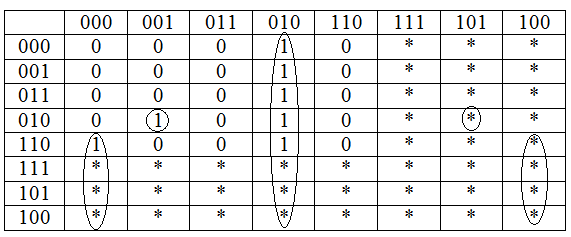
r0 = x₀x₁x₂ r₀x₁x₂ r₀r₁r₂x₁x₂

Составим функцию для r1:

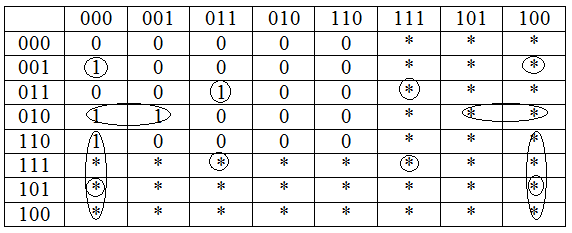
r1 = r₀x₁x₂ r₀r₁r₂x₁ r₁r₂x₁x₂r₁r₂x₁x₂

Составим функцию для r2:

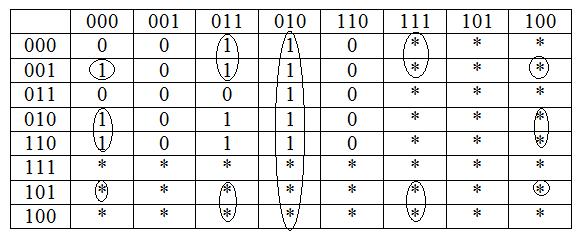
r2 = r₁r₂x₁x₂ r₁x₁x₂ x₀x₁x₂r₁r₂x₁x₂