
- •Лабораторная работа № 1 Тема: «Обработка одномерной выборки»
- •Краткие теоретические сведения
- •Контрольные вопросы
- •Порядок выполнения лабораторной работы
- •Задания к лабораторной работе
- •Лабораторная работа № 2 Тема: «Точечные и интервальные оценки характеристик генеральной совокупности»
- •Краткие теоретические сведения
- •Контрольные вопросы
- •Порядок выполнения лабораторной работы
- •Лабораторная работа № 3 Тема: «Сглаживание (выравнивание) статистических рядов»
- •Краткие теоретические сведения
- •Контрольные вопросы
- •Контрольные вопросы
- •Порядок выполнения лабораторной работы
- •Задания к лабораторной работе
- •Лабораторная работа № 5 Тема: «Проверка непараметрических статистических гипотез»
- •Краткие теоретические сведения
- •1, 4, 5, 8, 9, …, 7, 6, 3, 2.
- •Контрольные вопросы
- •Порядок выполнения лабораторной работы
- •Задания к лабораторной работе
- •Лабораторная работа № 6 Тема: «Проверка однородности выборочной совокупности»
- •Краткие теоретические сведения
- •Контрольные вопросы
- •Контрольные вопросы
- •Гипотезы об ожидаемых числах
- •Контрольные вопросы
- •Порядок выполнения лабораторной работы
- •Задания к лабораторной работе
Порядок выполнения лабораторной работы
Сформулировать приведенные в варианте задачи в терминах теории проверки статистических гипотез.
Представить графически по каждой задаче допустимую и критическую (критические) области, руководствуясь приведенным в условии задачи уровнем значимости.
Решить задачу, проверив сформулированные гипотезы всеми известными Вам и допустимыми для данной задачи непараметрическими критериями. Проанализировать и сопоставить результаты. Ответы сформулировать двумя способами: относительно принятия или отклонения основной гипотезы и относительно вопросов, поставленных в задаче.
Если объемы выборок различны, для возможного применения знакового критерия Вилкоксона доопределить выборку меньшего объема значениями, совпадающими с выборочным средним данной выборки для выравнивания мощностей выборок.
Задания к лабораторной работе
В качестве задания к лабораторной работе выбрать задачу из лабораторной работы № 4, которая представлена двумя выборочными совокупностями.
Лабораторная работа № 6 Тема: «Проверка однородности выборочной совокупности»
Цель работы: приобретение практических навыков в использовании непараметрических критериев для проверки однородности выборочной совокупности.
Краткие теоретические сведения
Критерий серий применяется для проверки гипотезы, утверждающей, что выборка однородна, т.е. элементы выборки получены случайным образом и независимы.
Описание критерия
Задана выборка ![]() .
.
Нулевая
гипотеза![]() :элементы выборки
получены случайным образом и независимы.
:элементы выборки
получены случайным образом и независимы.
Вычисление статистики критерия:
Построить вариационный ряд

По построенному вариационному ряду найти медиану
 :
:
![]() ,
еслиn=2k+1,
,
еслиn=2k+1,
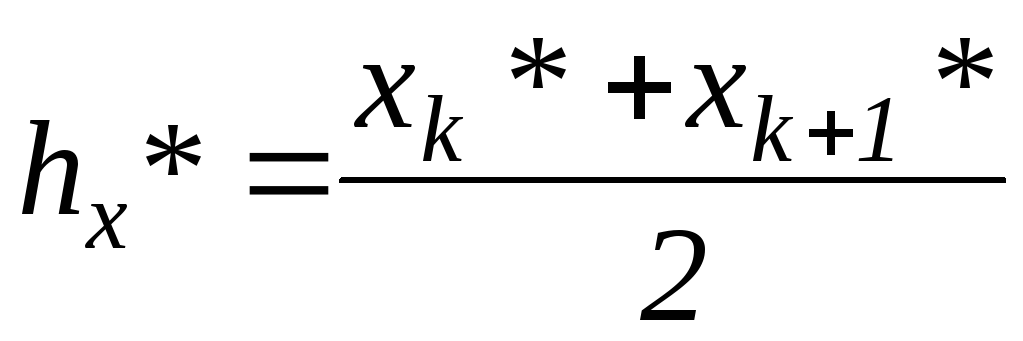 ,
еслиn=2k.
,
еслиn=2k.
Каждому элементу исходной выборки поставить в соответствие
«+»,
если элемент![]() ;
;
«-»,
если элемент![]() .
.
Если элемент исходного ряда совпадает с медианой, его необходимо удалить.
Для полученного ряда знаков ввести обозначения
![]() - количество «+»;
- количество «+»;
![]() - количество «-»;
- количество «-»;
N - число серий. Серией в этом наборе называется всякая последовательность, состоящая из одинаковых знаков и ограниченная противоположными знаками, либо находящаяся в начале или конце набора.
Если
 ,
то для проверки можно использовать
статистику критерия вида:
,
то для проверки можно использовать
статистику критерия вида:

Нулевая гипотеза принимается на уровне значимости
 ,если выборочное
значение статистики удовлетворяет
одному из неравенств:
,если выборочное
значение статистики удовлетворяет
одному из неравенств:
Двусторонний
критерий: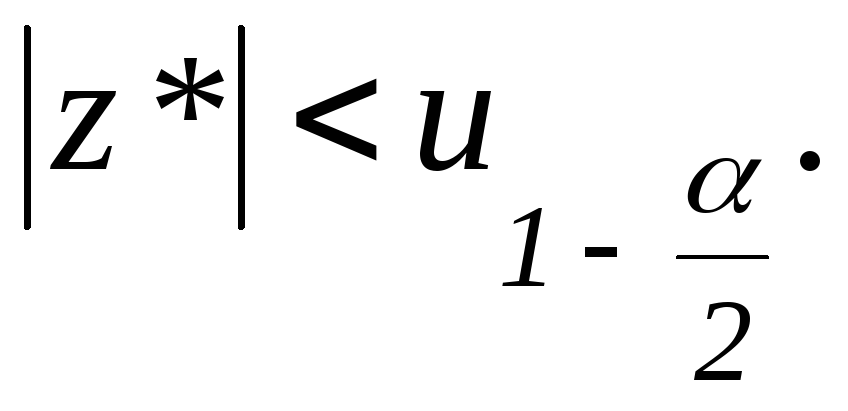
Правосторонний
критерий:![]()
Левосторонний
критерий: ![]()
В этом случае выборка однородна.
Пример 1. Измерение напряжения пробоя у диодов, полученного в результате новой серии испытаний, дало следующие результаты (в вольтах):
3,21; 2,82; 2,66; 1,9; 2,45; 2,32; 2,27; 2,14; 2,08; 2,01; 2,0; 2,77; 1,99; 2,02; 2,03; 2,09; 2,15; 2,23; 2,34; 2,62; 1,9; 2,0.
Можно ли считать
полученные значения случайными? Принять
![]() =0,01.
=0,01.
Построим вариационный ряд
1,9; 1,9; 1,99; 2,0; 2,0; 2,01; 2,02; 2,03; 2,08; 2,09; 2,14; 2,15; 2,23; 2,27; 2,32; 2,34; 2,45; 2,62; 2,66; 2,77; 2,82; 3,21.
Медиана ![]() :
:![]()
Исходному ряду наблюдений соответствует следующая последовательность знаков:
+ + + - + + + - - - - + - - - - + + + + - - , где n1=11, n2=11, N=8.

Так как  нулевая гипотеза
принимается: можно считать, что данная
последовательность получена из
совокупности случайных последовательностей.
нулевая гипотеза
принимается: можно считать, что данная
последовательность получена из
совокупности случайных последовательностей.
