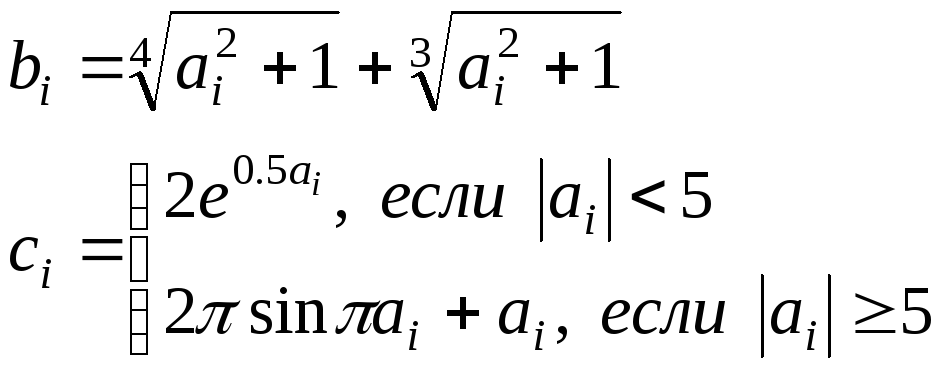- •Павлыш в.Н., Ефименко к.Н., Добровольский ю.Н.
- •1. Алгоритмы и способы их описания
- •2. Алгоритмы линейной структуры
- •3. Алгоритмы разветвляющейся структуры
- •4. Алгоритмы циклической структуры
- •4.1. Структура и основные типы циклов
- •4.2. Алгоритмы нахождения суммы, произведения и количества вычисленных значений
- •4.3. Циклы с неизвестным числом повторений
- •4.4. Вложенные циклы
- •5. Алгоритмы обработки одномерных массивов
- •5.1. Ввод и вывод элементов одномерного массива
- •5.2. Нахождение максимального и минимального элементов массива
- •5.3. Сортировка элементов массива
- •5.4. Циклический сдвиг элементов массива
- •5.5. Добавление и удаление элементов массива
- •6. Алгоритмы обработки двумерных массивов
- •7. Алгоритмы, содержащие вспомогательные подзадачи
- •Задания к контрольной работе Задание №1.Организация линейного и разветвляющегося
- •Варианты заданий.
- •Задание №2. Организация циклов с известным числом повторений
- •Варианты заданий.
- •Задание № 3. Организация циклов с неизвестным числом повторений
- •Варианты заданий.
- •Задание № 4. Организация вложенных циклов
- •Варианты заданий.
- •Задание № 5. Обработка одномерных массивов
- •Задание № 6. Обработка двумерных массивов
- •Варианты заданий.
- •Задание № 7. Использование процедур и функций
- •Варианты заданий.
- •Рекомендации к выполнению контрольной работы
- •Методическое пособие «основы алгоритмизации»
- •Составители: Павлыш Владимир Николаевич, д.Т.Н., проф. Ефименко Константин Николаевич, к.Т.Н., доц.
Задание № 4. Организация вложенных циклов
Задание. Составить блок-схему алгоритма и программу решения поставленной задачи, которая в соответствии с исходными данными вычисляет значения заданных выражений.
П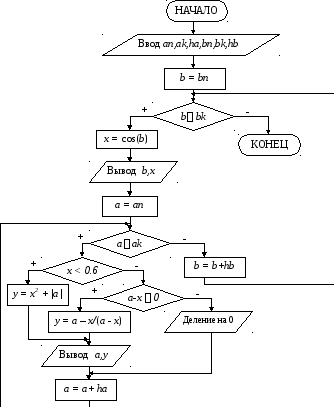
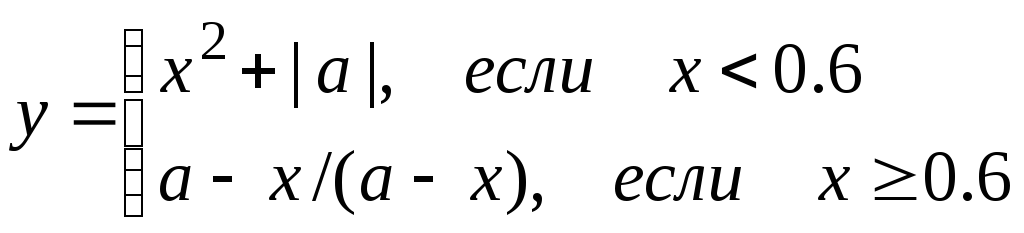 ример.Составить алгоритм и программу для
вычисления значенийx
иупри всех возможных
значенияхaиb,
которые лежат в интервале отanдоakс шагомhaи отbnдоbkс шагомhb,
соответственно.
ример.Составить алгоритм и программу для
вычисления значенийx
иупри всех возможных
значенияхaиb,
которые лежат в интервале отanдоakс шагомhaи отbnдоbkс шагомhb,
соответственно.
Блок-схема алгоритма:
Программа на языке Турбо Паскаль:
ProgramPr4;
Labelm1;
Var a, an, ak, ha, b, bn, bk, hb, x, y: real;
Begin
Write(‘Ввод an, ak, ha, bn, bk, hb’); Readln(an, ak, ha, bn, bk, hb);
b:=bn;
While b <= bk do Begin
x := cos(b); writeln(‘b=’, b : 6 : 2, ‘ x=’, x : 6 : 2);
a := an;
While a <= ak do Begin
If x < 0.6 Then y := Sqr(x) + Abs(a)
Else If a – x < > 0 Then y := a – x / (a – x)
Else Begin Writeln(‘Деление на 0’); Goto m1; End;
writeln(‘a=’, a : 6 : 2, ‘ y=’, y : 6 : 2);
m1: a := a + ha; End;
b := b + hb; End;
End.
Варианты заданий.
|
№ п/п |
Модель |
Исходные данные |
Выводимые данные |
|
1 |
2 |
3 |
4 |
|
1 |
|
x, 1 ≤ a ≤ 2; ha=0.1 - 3 ≤ b ≤ 1, hb=1 |
a,b,y |
|
2 |
|
0.6 ≤ a ≤ 1.2 -0.3≤ b ≤ 1.2 ha=0.2; hb=0.3 |
a, b x, z, |
|
3 |
|
3 ≤ a ≤ 6 ha = 1 0.2 ≤ x ≤ 1 hx = 0.2 |
a, x, y, z |
|
4 |
|
1.2 ≤ c ≤ 2 2 ≤ x ≤ 8 hc = 0.2; hx = 2 |
c, x, a, z |
Продолжение таблицы к заданию 4
|
1 |
2 |
3 |
4 |
|
5 |
x=3k+2 |
1.4 ≤ b ≤ 2.6 hb = 0.3; p = 0.4 1 ≤ k ≤ 7; hk = 3 |
b, k, x, z |
|
6 |
|
3 ≤ k ≤ 15 hk = 4 2 ≤ b ≤ 4 hb = 0.5, a |
k, b, x, z |
|
7 |
x=k2+k+0.1 |
2.2 ≤ a ≤ 4.2 ha = 0.5
hk = 0.4 |
a, k, x, z |
|
8 |
|
b = 7 0.5 ≤ a ≤ 2 -1.2≤ t ≤ 0.4 ha=0.5; ht=0.4 |
a, t, x, z |
|
9 |
|
1 ≤ a ≤ 2 ha = 0.5 - 5 ≤ t ≤ 7 ht = 3 |
a, t, x, z |
|
10 |
|
4 ≤ x ≤ 6; hx = 1 1 ≤ k ≤ 6.1 hk = 1.7 |
x, k, b, z |
|
11 |
|
hx = 2 1 ≤ a ≤ 2 ha = 0.5 |
a, x, z |
Продолжение таблицы к заданию 4
|
1 |
2 |
3 |
4 |
|
12 |
|
3 ≤ c ≤ 5 hc = 0.5
hi = 0.5 |
c, i, x, z |
|
13 |
|
ha = 1
hk = 1.5 |
a, k, x, z |
|
14 |
|
4 ≤ b ≤ 8 hb = 1 1 ≤ t ≤ 2.5 ht = 0.5 |
b, t, x, z |
|
15 |
|
5 ≤ a ≤ 7 ha = 1 0.5 ≤ t ≤ 2 ht = 0.5 |
a, t, x, z |
|
16 |
|
1.5 ≤ a ≤ 2.5 ha = 0.5 1.5 ≤ t ≤ 4.5 ht = 1.5 |
a, t, x, z |
|
17 |
|
2 ≤ a ≤ 3 1.2 ≤ k ≤ 2.8 ha=0.5 hk=0.4 |
a, k, x, z |
|
18 |
|
4 ≤ t ≤ 8.5 3.7 ≤ b ≤ 4.7 ht=2.5 hb=0.5 |
t, b, x, z |
Продолжение таблицы к заданию 4
|
1 |
2 |
3 |
4 |
|
19 |
|
a=10.3 0.3 ≤ b ≤ 1.3 hb=0.5 1 ≤ x ≤ 3;hx=0.5 |
b, x, z |
|
20 |
|
a, c 1 ≤ b ≤ 3; hb = 1 1 ≤ i ≤ 3; hi=1.5 |
b, i, x, z |
Задание № 5. Обработка одномерных массивов
Задание. Составить блок-схему алгоритма и программу решения поставленной задачи, которая в соответствии с исходными данными вычисляет значения заданных выражений.
Пример. Составить алгоритм и программу формирования массиваYна основе исходного массива Х размерностьюN. Определить максимальный положительный элемент массиваY. Элементы массиваYвычисляются по формуле:
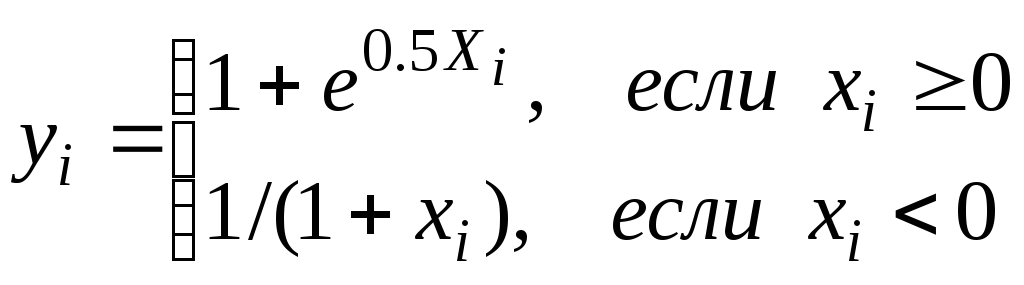
Программа на языке Турбо Паскаль:
Program Pr5;
Var x, y: array [1..20] of real;
i, N, imax: byte;
Begin
Write(‘Ввод N’); Readln(N);
for i:=1 to N do begin
Write(‘Ввод x[’, i, ’] =’); Readln(x[i]);
end;
imax := 0;
for i:=1 to N do begin
if x[i] >= 0 then y[i] := 1+exp(0.5*x[i])
else
if 1+x[i] <> 0 then y[i] := 1/(1+x[i])
else begin writeln(‘Аномалия’); y[i] := 0
end;
writeln(‘y[‘, i, ’]=’, y[i] : 6 : 2);
if y[i] > 0 then
if imax = 0 then imax := i
else if y[imax] < y[i] then imax := i;
end;
 writeln(‘y[’, imax, ‘]=’, y[imax] : 6 : 2);
writeln(‘y[’, imax, ‘]=’, y[imax] : 6 : 2);
End.
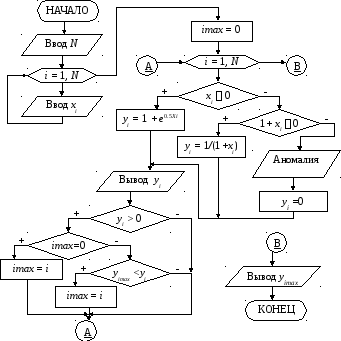
Блок-схема алгоритма:
Варианты заданий.
|
№ п/п |
Модель |
Исходные данные |
Выводимые данные |
|
1 |
2 |
3 |
4 |
|
1 |
|
Массив X i = 110 |
Массив Y Значение наибольшего отрицательного элемента массива Y |
|
2 |
|
Массив Y i = 115
|
Массив z. Максимальный элемент zmax и номера элементов массива Z меньших 0.5zmax |
|
3 |
|
Массив X 1 ≤ xi ≤ 10 hxi=1
|
Массивы Z,Y. Сумма и количество положительных элементов массива Y. Среднее арифметическое отрицательных элементов массива Y. |
|
4 |
|
Массив X -1 ≤ xi ≤ 11 hxi=2
|
Массивы z, Y. Порядковый номер и значение первого положительного числа в массиве Z. |
|
|
yi
=
Все отрицательные элементы массива Y заменить нулями, а нулевые элементы заменить значением элемента xi |
Массив X i = 115 |
Массив Y до и после замены. Среднее арифметическое массива Y до и после замены. |
Продолжение таблицы к заданию 5
|
1 |
2 |
3 |
4 |
|
6 |
|
Массив X i = 115 |
Массив Y. Значение и номер эл-та yi, наиболее отличающегося от S. |
|
7 |
сi=max(ai, bi )-min(ai, bi ) |
Массив X i = 110 |
Массивы A,B,C. максимальный элемент массива C среди четных элементов. |
|
8 |
|
Массив X i = 125
|
Массив M. Разность между S и P. |
|
9 |
Если maxPi меньше суммы всех остальных элементов, то присвоить этому элементу значение 0. |
Массив X -0.4≤ xi ≤1.2 hxi=0.2
|
Массив P, maxРi. |
|
10 |
|
Массив Y i = 111
|
Массивы X, P. Значения и номера мин. и макс. по модулю элементов P. |
|
11 |
|
t
|
Массив Y. Сумма и количество элементов массива Y, лежащих на отрезке [0;2]. |
Продолжение таблицы к заданию 5
|
1 |
2 |
3 |
4 |
|
12 |
Элементы Zi сгладить по формуле: Zi = (Zi-1 + Zi + Zi+1)/3 |
Массив X i = 115 |
Массив Z до и после сглаживания. |
|
13 |
|
Массив X -5 xi 4 hxi=0.9
|
Массивы X, A. S, P. Количество аi<0. |
|
14 |
Считать пары точек (yi, zi) координатами точек на плоскости YOZ |
Массив X i = 110 |
Массивы Y, Z. Определить, какая из точек 2, 3…10 наиболее удалена от точки (y1, z1). |
|
15 |
Заменить все отрицательные элементы массива Y суммой R и значения соответствующего элемента. |
Массив A i=111 |
Массив Y до и после замены. Ср. арифметическое (R) элементов массива Y. |
|
16 |
|
R, V0, Y0, Массив X i=110 |
R, V0, Y0, PR. Массивы Y,V. |
Продолжение таблицы к заданию 5
|
1 |
2 |
3 |
4 |
|
17 |
Cчитать ai, bi, ci коэффициентами квадратного уравнения ax2+bx+c=0 |
Массив A i=120 |
Массивы B,C. Порядковые номера уравнений, имеющих комплексные корни. |
|
18 |
Считать значения элементов массива Aи B длинами полуосей эллипса a и b. |
Массив X 4 ≤ xi ≤ 12 hxi=2
|
Массивы A,B. Порядковый номер N эллипса, площадь которого S= a b наибольшая.
|
|
19 |
|
Массив X i=1÷12 |
Массив Y. Индекс элемента, наиболее близкого по значению к ср. геометрическому (Р) массива Y. |
|
20 |
|
Массив X -0.3≤ xi ≤1.2 hxi=0.3 |
Массив Y. Среднее арифметическое (А) массива Y и количество yi >A. |

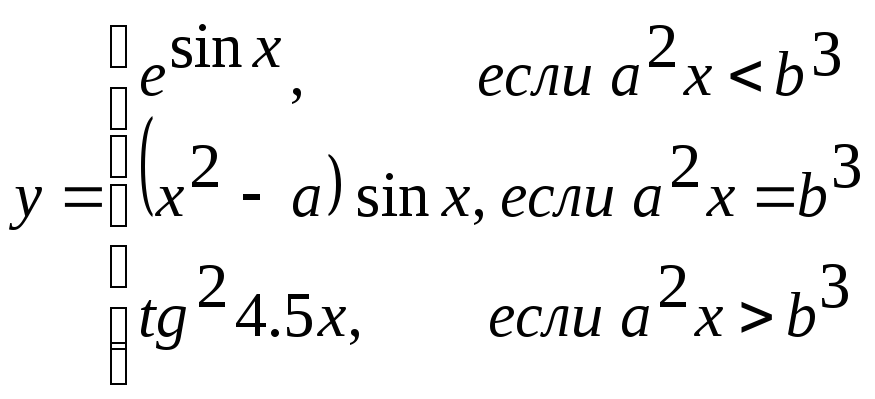
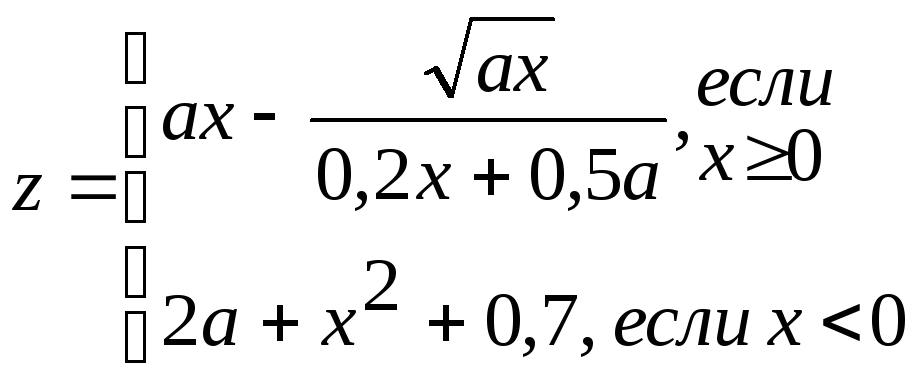
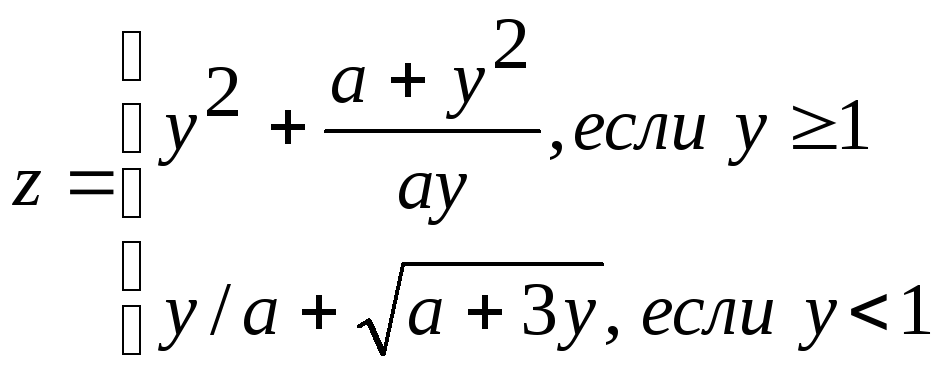
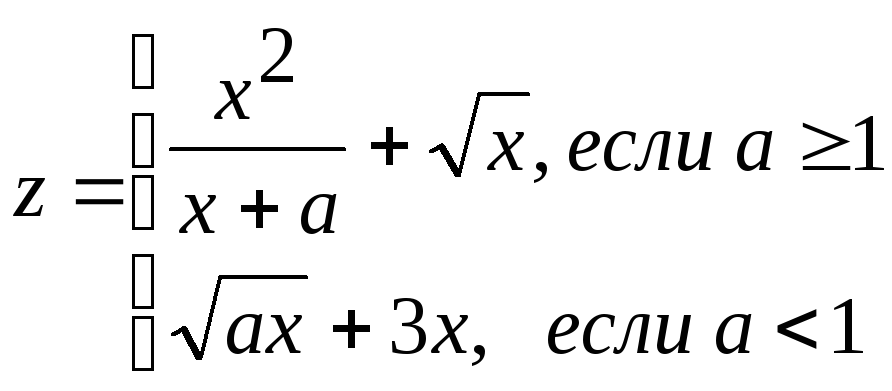
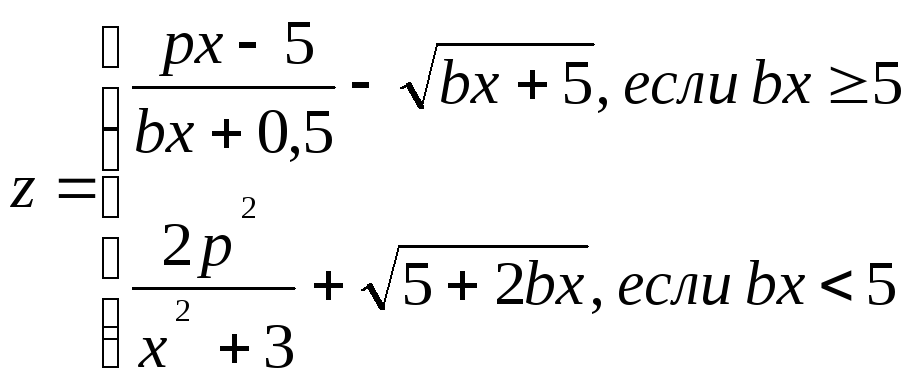
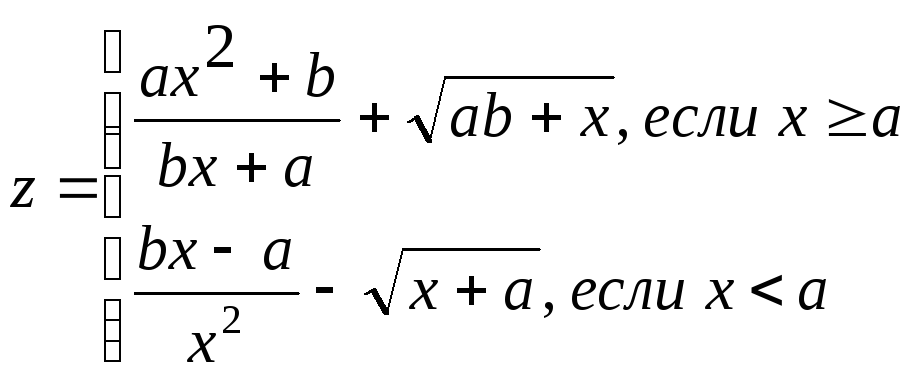
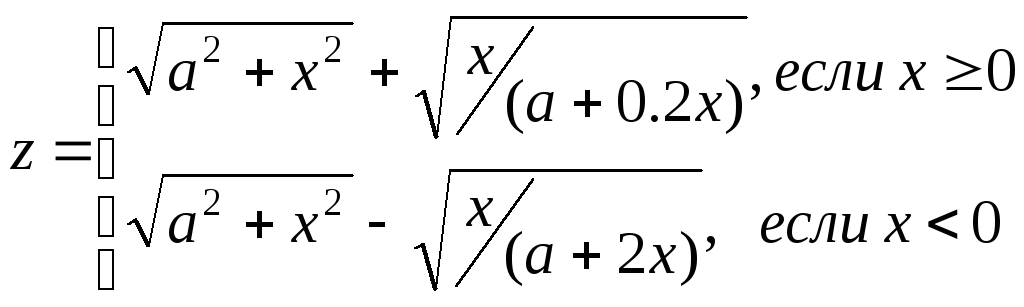
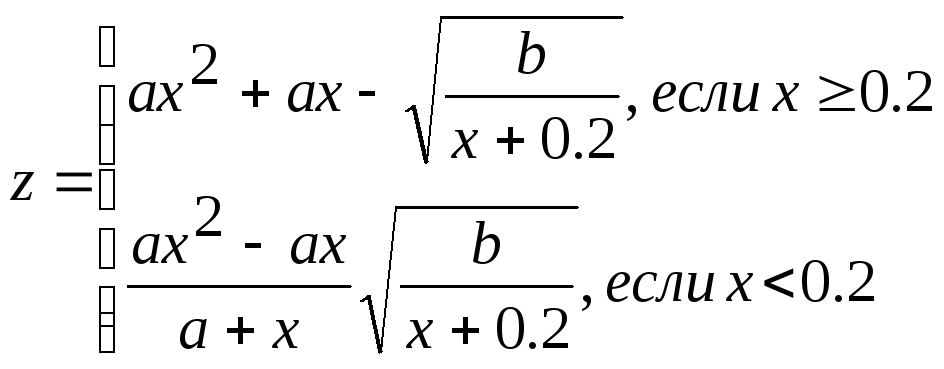
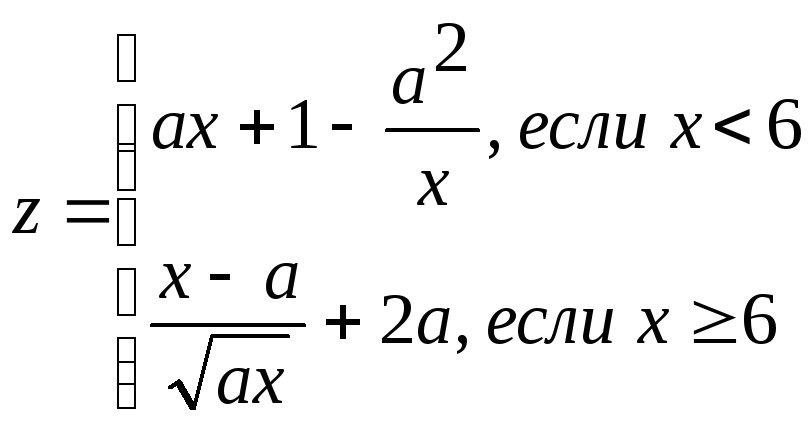
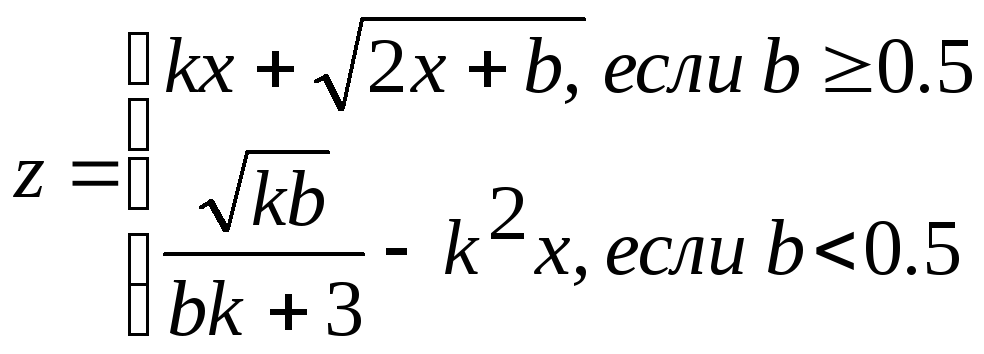
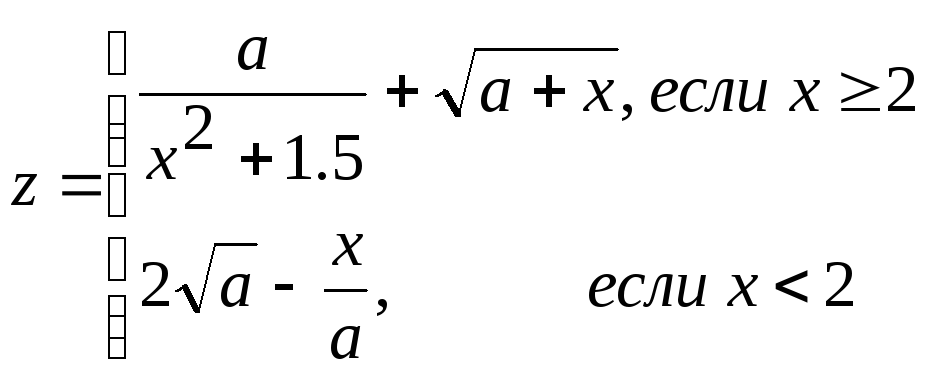
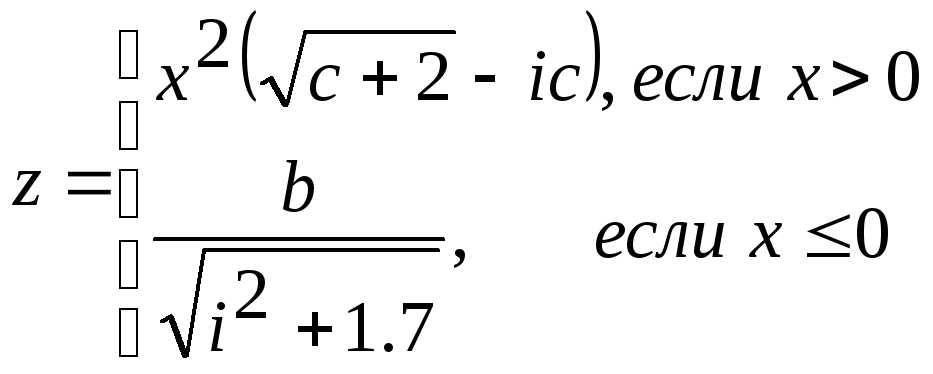
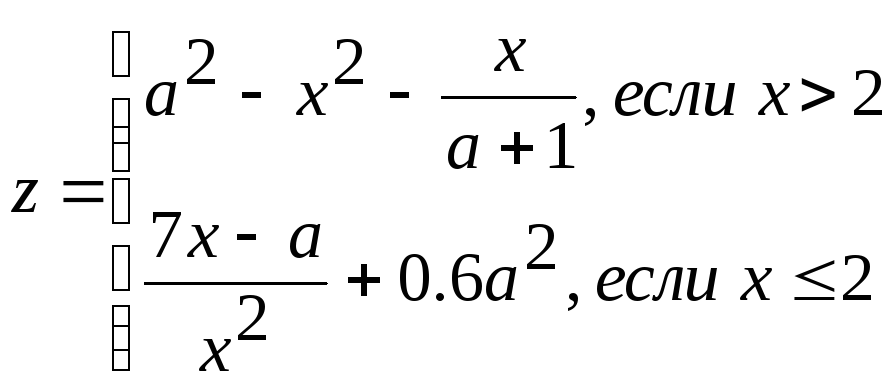
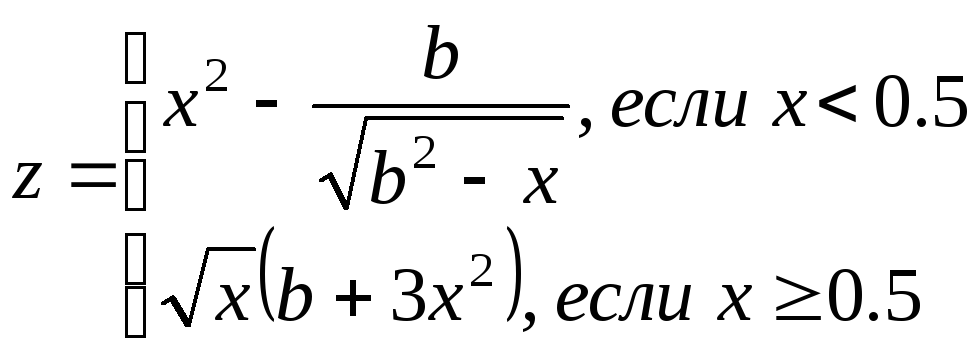
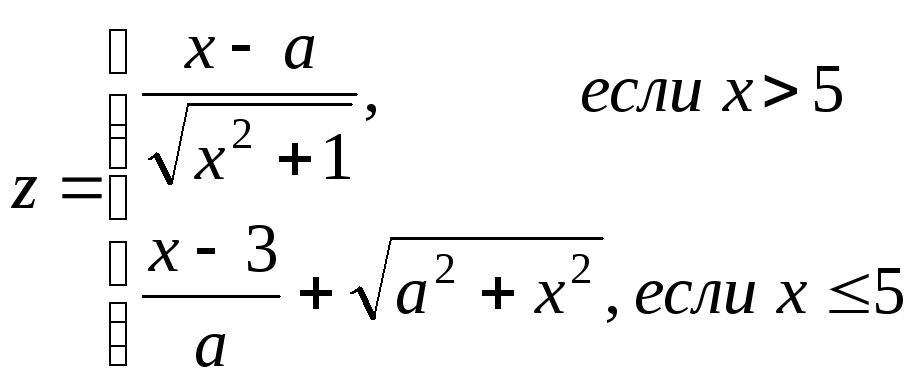
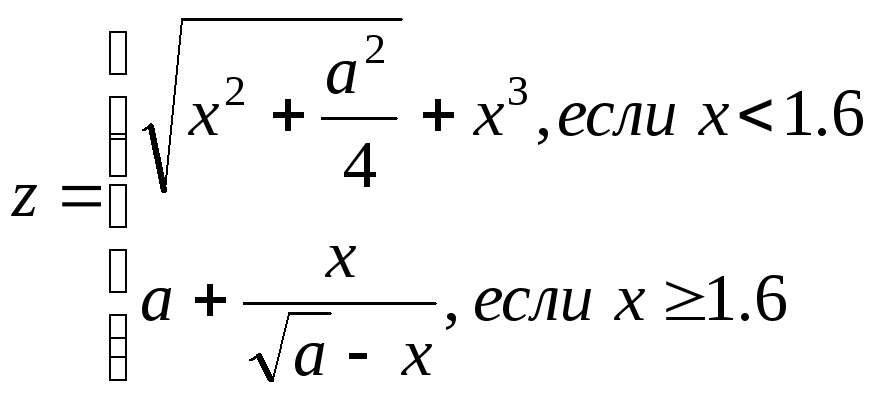
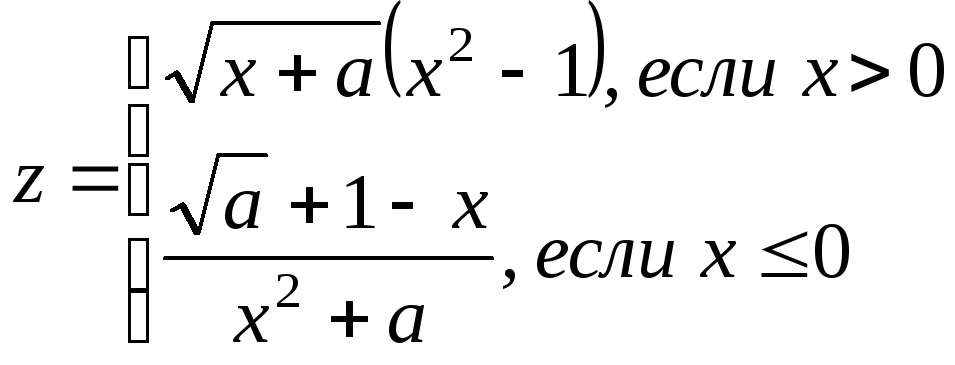
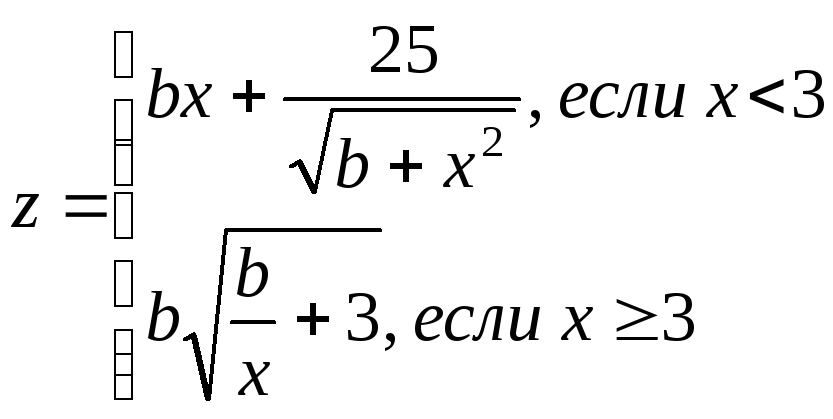
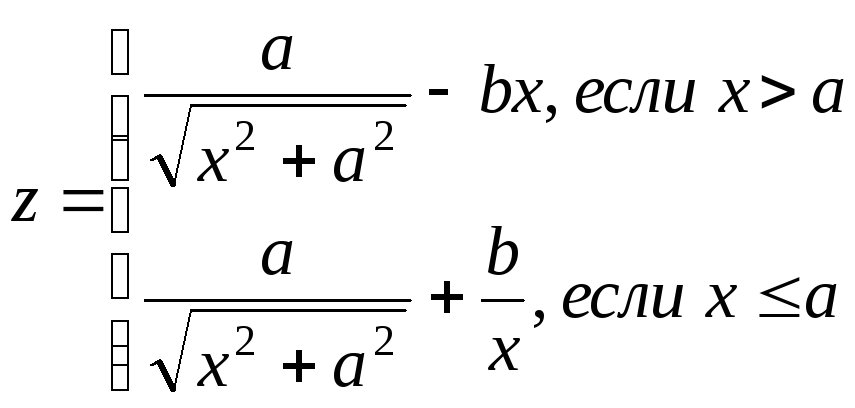
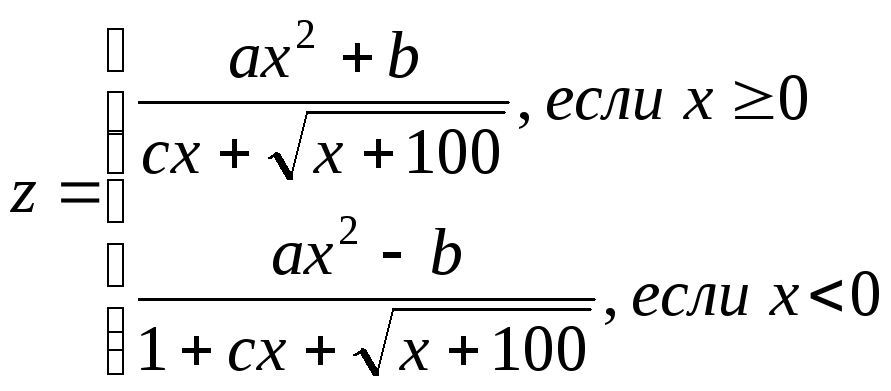 x=(i-a)/i
x=(i-a)/i
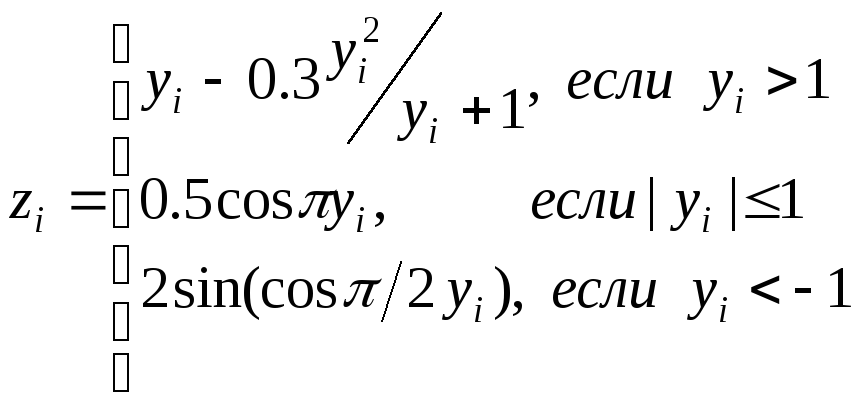
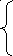 yi
=
yi
=
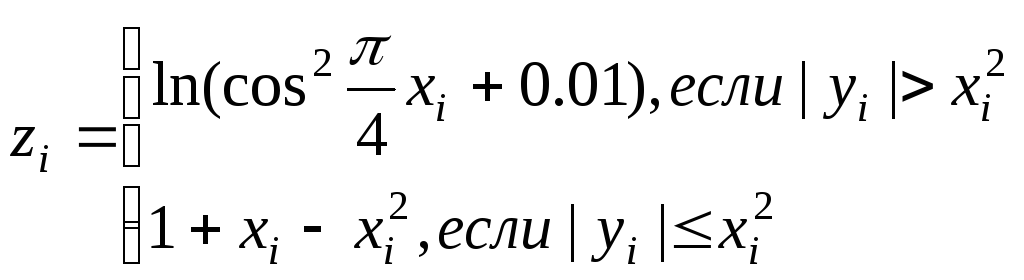
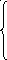 5
5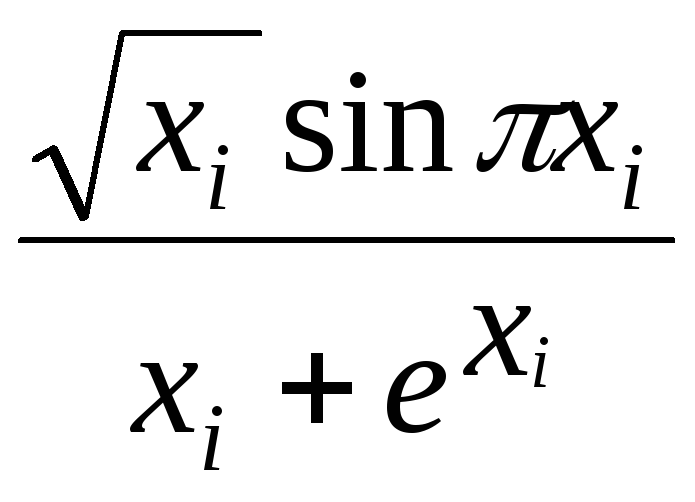 , если xi
> 1.5
, если xi
> 1.5 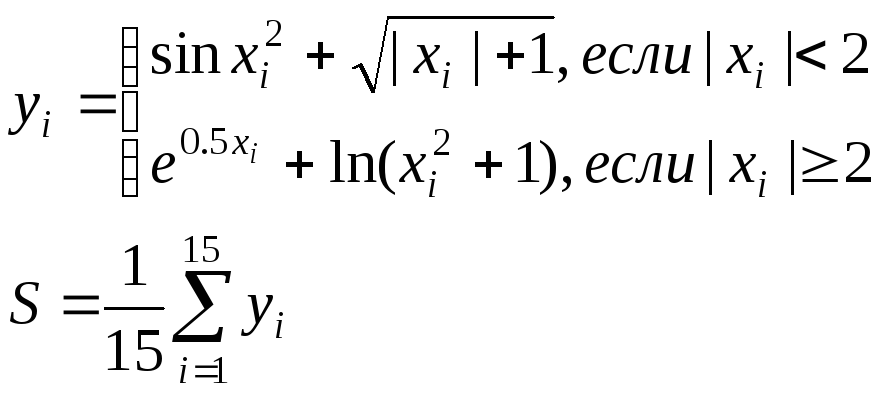
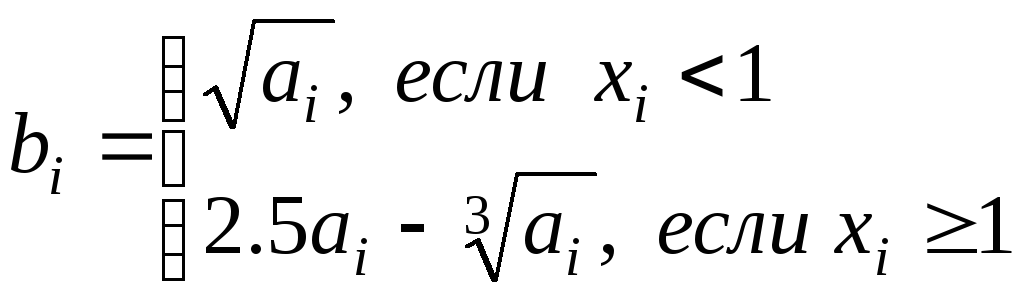
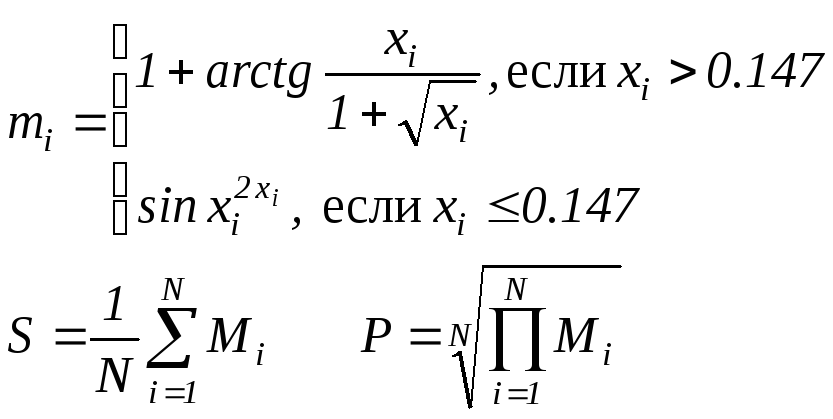
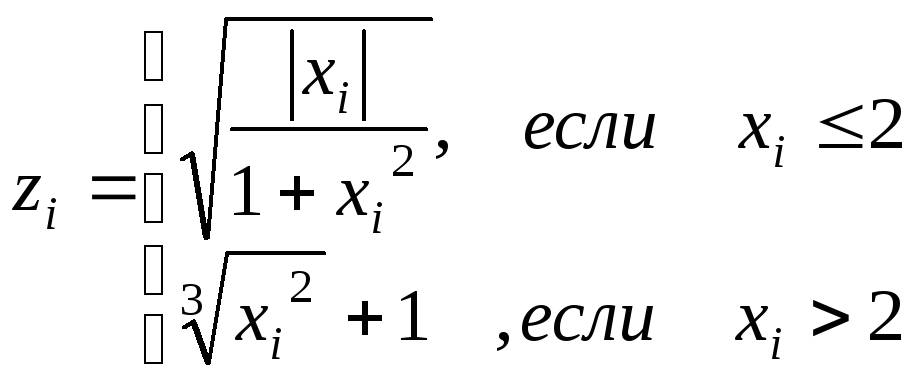
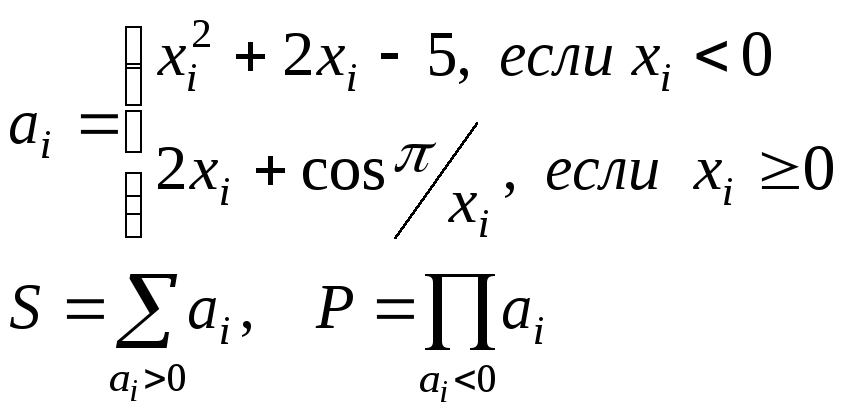
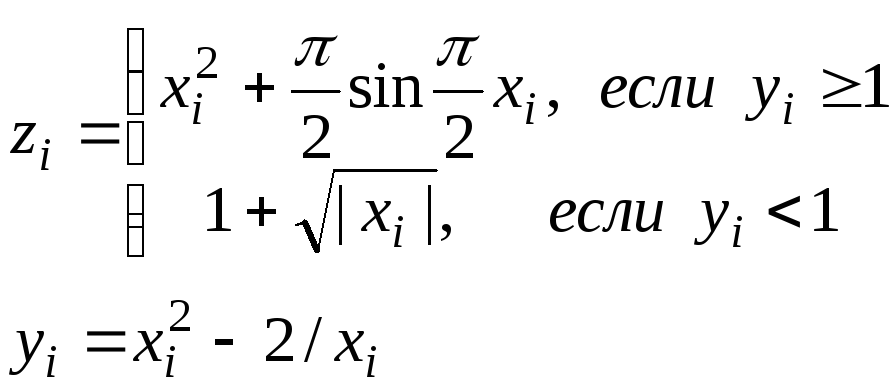
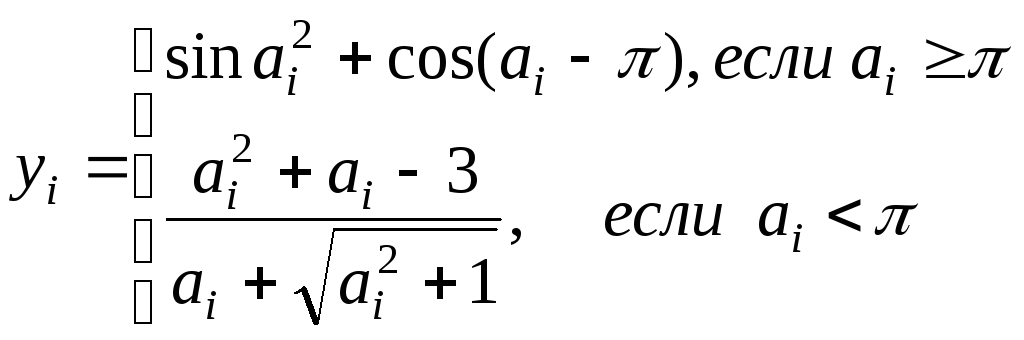
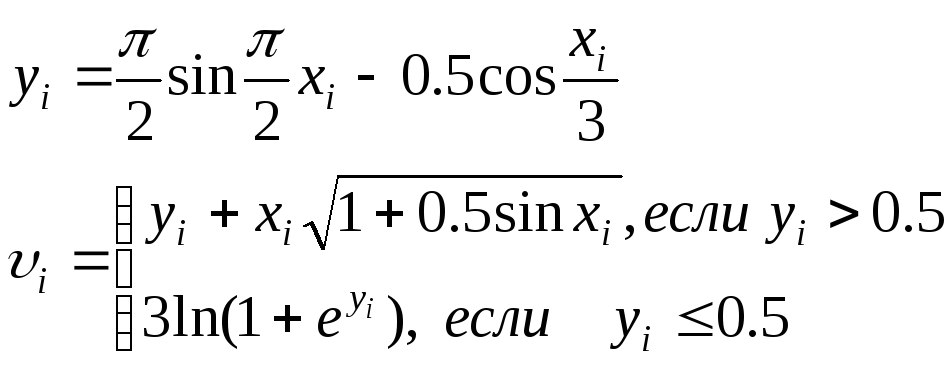 Считать
(Vi
,Yi
) координатами точек плоскости.
Определить процент (PR)
точек, лежащих в круге радиусом R
с центром в точке(V0
,Y0).
Считать
(Vi
,Yi
) координатами точек плоскости.
Определить процент (PR)
точек, лежащих в круге радиусом R
с центром в точке(V0
,Y0).