4.Примеры решения задач.
Пример1. Плоский конденсатор площадью пластин S и стеклянной пластинкой толщиной d заряжен до разности потенциалов U и отключен от источника напряжения. Какую работу нужно совершить, чтобы вынуть пластинку из конденсатора?
Дано: S,d,U,ε
Определить А.
Решение. Работу по удалению пластинки из конденсатора находим как разность начальной и конечной энергии заряженного конденсатора.
где
-
энергия конденсатора после удаления
пластинки;
- энергия конденсатора до удаления
пластинки.
Поскольку конденсатор отсоединен от источника напряжения, то заряд останется прежним.
Выразим энергию
конденсатора
и
через заряд и емкость:
Тогда т.к.
,
где ε – диэлектрическая проницаемость
стекла.
Проверим единицы измерения А:
Ответ:
Пример 2. Генератор с ЭДС ε=140 В и внутренним сопротивлением r=0,2 Ом дает ток I=100А. Сопротивление внешней цепи R=1,2 Ом. Определить полную и полезную мощность генератора, потери мощности и КПД. Составить уравнения баланса мощностей.
Дано: ε=140 В, r=0.2 Ом, I=100A, R=1,2 Ом
Определить:
,P,
ΔP
и КПД
Решение. Полная мощность генератора:
(1)
где I – сила тока; ε – ЭДС.
Полезная мощость:
(2)
где U – разность потенциалов на концах цепи.
Учитывая, что
(3)
где r – внутреннее сопротивление источника тока
Имеем:
(4)
Потери мощности во внешней цепи
(5)
КПД:
(6)
Проверим единицы измерения искомых величин:
Подставляя в (1,4,5 и 6) числовые значения и вычисляя получим:
Вт=14 (кВт)
(Вт)=12 (кВт)
ΔP=14-12=2 (кВт)
Проверим уравнение баланса мощностей:
Ответ:
=
14 кВт;P
= 12 кВт; ΔP=2
кВт; η=85,7%
Пример3.
Сила тока в проводнике сопротивлением
R=50
Ом равномерно растет от
=0
до
=3А
за время τ=6c.
Определить выделившееся в проводнике
за это время количество теплоты.
Дано:
R=50
Ом,
,
,
τ=6 c
Определить Q.
Решение. Согласно закону Джоуля-Ленца в случае бесконечного промежутка времени
По условию задачи сила тока равномерно растет, т.е.
где коэффициент
пропорциональности
Тогда можно записать:
(1)
После интегрирования (1) с учетом выражения для K получим:
(2)
Проверим единицы измерения Q:
Подставив в (2) числовые значения и вычисляя получим:
Ответ: Q=900 Дж
Пример4.
Плотность электрического тока в медном
проводе равна 10
.
Определить удельную тепловую мощность
тока, если удельное сопротивление меди
Дано:
,
Определить ω.
Решение. Согласно законам Джоуля-Ленца и Ома в дифференциальной форме,
(1)
(2)
где γ и ρ – соответственно удельные проводимость и сопротивление проводника;
E – напряженность электрического поля;
ω – удельная тепловая мощность тока.
Из закона (2) получим, что E= ρ γ. Подставив это выражение в (1), найдем искомую величину тепловой мощности тока.
(
3)
Проверим единицы измерения ω:
[ω]
=
Подставив в (3) числовые значения и вычисляя получим:
Ответ:
Пример 5. Между обкладками плоского конденсатора, заряженного до разности потенциалов 1,5 кВ, зажата парафиновая пластинка (ε=2) толщиной 5 мм.
Определить поверхностную плотность связанных зарядов на парафине.
Дано:
U=1,5кВ=1,5
В;
ε=2;d
= 5мм =
м.
Определить
.
Решение.
Так как векторы
и
нормальные
к поверхности диэлектрика, то
;
;
Тогда можно записать
(1)
Где
и
соответственно
векторы электрического смещения и
напряженности поля плоского конденсатора;
- вектор
поляризованности диэлектрика. P
=
,
т.е. равен поверхностной плотности
связанных зарядов диэлектрика.
Тогда
Отсюда
(2)
Учитывая, что
и
,
гдеd
– расстояние между обкладками
конденсатора, получим:
(3)
Проверим единицы
измерения
Подставив в (3) числовые значения и вычисляя получим:
Ответ:
Пример 6.
Расстояние l
между двумя точечными зарядами
=1нКл
и
=-2нКл,
расположенными в вакууме, равно 10 см.
Определить:
Напряженность E;
Потенциал φ поля, создаваемого этими зарядами в точке А, удаленной от первого заряда на расстояние
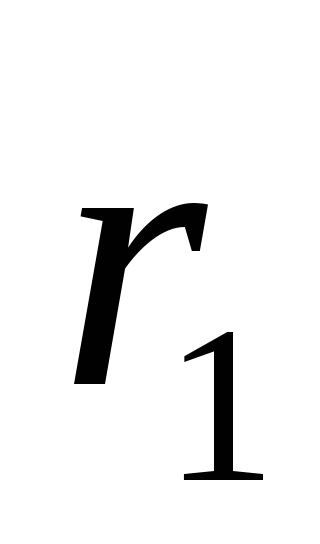= 9 см. и от второго заряда на
=7
см.
Дано:
l=10
см = 0.1 м;
=1нКл=
Кл;
=-2нКл=
Кл;
= 9 см=0,09 м;
=7
см.=0,07 м.
Определить: 1)Е; 2) φ;
Решение. Согласно
принципу суперпозиции
.
Направления векторов указаны на рис.1.
Модуль вектора
найдем по теореме косинусов:
Рис.4.1
,
(1)
где
(2)
В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:
(3)
Напряженности
электрического поля, создаваемые в
вакууме зарядами
и
:
,
(4)
Подставив (4) и (3) в формулу (1), получим искомую напряженность:
(5)
Согласно принципу суперпозиции, потенциал результирующего поля
(6)
где
и
- потенциалы полей создаваемых
соответственно
зарядами
и
.
Тогда
(7)
Проверим единицы измерения Е и φ.
Подставив в (5) и (7) числовые значения и вычисляя получим:
Ответ: E=3,57 кВ/м, φ=-157 В
Пример 7.Две концентрические проводящие сферы радиусами R1=6 см и R2=10 см несут соответственно заряды Q1=1 нКл и Q2=-0.5 нКл. Найти напряженность поля в точках, отстоящих от центра сфер на расстояниях r1=5 см, r2=9 см и r3=15 см. Построить график E(r).
Дано: R1=0.06 м, R2=0.1 м, Q1=10-9 Кл, Q2=-5*10-10 Кл, r1=5*10-2 м, r2=9*10-2 м, r3=15*10-2 см.
Е1–?,
Е2–?, Е3–?, Е(r)–?
1
.
Для определения напряженности Е1
проведем гауссовую поверхность S1
радиусом r1
, рис.
2 и воспользуемся теоремой
Остро-градского-Гаусса :
(т.к. суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю). Рис 4.2
Следовательно,
и Е1
во всех точках, удовлетворяющих условию
r1<R1,
будет равна нулю.
2. Проведем гауссовую поверхность радиусом r2 ,рис.2.
(так как внутри гауссовой поверхности находится только заряд Q1).
Из соображений симметрии En=E2=const, то Е2 можно вынести за знак интеграла:
или
,
где
– площадь гауссовой поверхности.
3. Проведем гауссовую поверхность радиусом r3
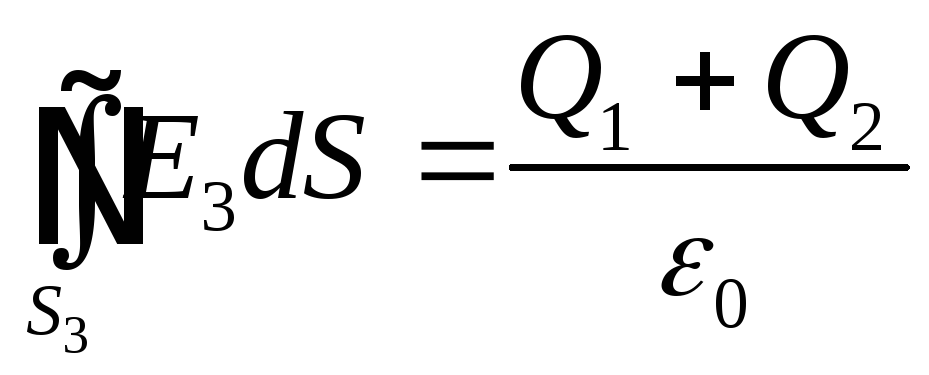
(так как внутри гауссовой поверхности находятся заряды Q1 и Q2)
–площадь
гауссовой поверхности
Получим:
Построим график E(r),рис.3
1)
r<R1,
2)
r=R,
Рис.4.3
.
E2(r)
изменяется по закону
.
r=R2;
3) r=R2;
Таким образом, функция E(r) в точках r=R1 и r = R2 терпит разрыв.
Ответ:
Е1=0,
Е2=1.11
,
Е3=200
.
Пример8.
На расстоянии
=4
см от бесконечно длинной заряженной
нити находится точечный зарядq=0,66
нКл. Под действием поля заряд приближается
к нити до расстояния
=2
см. При этом совершается работа
Дж.
Найти линейную плотность
заряда на нити.
Дано:
=4см=
м;
=2
см=
м;q=0,66нКл;
А=
Дж
Определить: τ
Решение. Работа, совершаемая силами элекrтрического поля при перемещении заряда
где dU=-E dr;
- напряженность
поля бесконечно длинной заряженной
нити.
Тогда
Проинтегрировав
это выражение получим:
Отсюда
Проверим единицы измерения τ:
Подставив числовые значения и вычисляя получим:
Ответ:
.
Пример 9. На тонком стержне длинной l=20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а=10 см от ближайшего конца находиться точечный заряд Q1 =40 нКл, который взаимодействует со стержнем с силой F=6 мкН. Определить линейную плотность заряда на стержне.
Дано:
l=0,2
м, а=0,1
м, Q1=40нКл=4
Кл
Определить: τ.
Решение. Согласно закону Кулона сила взаимодействия двух точечных зарядов
Где ε =1 – диэлектрическая проницаемость среды,
ε
-
электрическая
постоянная,
r - расстояние между зарядами.
Т.к. заряд на стержне не является точечным, поэтому на стержне рис.4 выделим малый участок dr c зарядом dQ= τdr , где τ- линейная плотность заряда на стержне.Получим:
dr
r
l a
Рис.4.4
Интегрируя это выражение в пределах от а до а+l , получаем
Откуда:
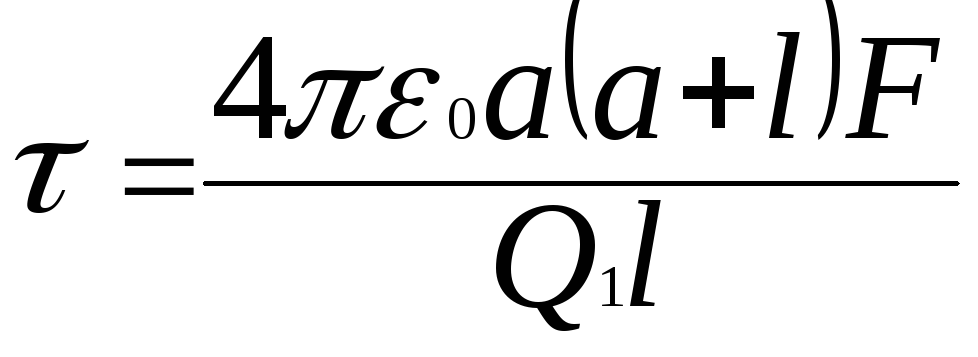
Проверим единицы измеренияй:
Подставив числовые значения и вычисляя, получим:
Ответ:
Пример
10.
Определить силу тока, текущего через
элемент ε
,
если ε
= 1 В,
ε
= 2 В, ε
= 3 В,r
= 1 Ом,r
= 0.5 Ом,r
= 1/3 Ом,R
= 1 Ом,R
= 1/3 Ом.
Дано:
ε
= 1 В, ε
= 2 В, ε
= 3 В,r
= 1 Ом,r
= 0.5 Ом,r
= 1/3 Ом,R
= 1 Ом,R
= 1/3 Ом. ОпределитьI
.
B
Выберем
произвольно
направления
токов в ветвях (см. рис.5).
К решению задачи применим законы
Кирхгоффа. По первому закону
Кирхгоффа для узла А имеем:
– I
Недостающие
уравнения со- ставляем по второму
закону Кирхгоффа. В данной схеме три
контура: ABCA,
ACDA,
ABCDA.
Выберем направление обхода кон-
+
I
+
I
= 0
(1)
ε
,r
C
ε
,r
I
R
I
ε
,
r
А
R
Д
Рис.4.5
для контура ABCA
– I
r
–
I
R
–
I
r
=
ε
–
ε
(2)
для контура ADCA
I
r
–
I
R
–
I
r
=
ε
–
ε
(3)
Подставив в (2) и (3) числовые значения сопротивлений и ЭДС получим систему уравнений:
I
=
I
+
I
(4)
2I
+
0.5I
= 1 (5)
– 0.5I
+
2/3I
=
1
(6)
Из (4) и (5) следует
0.5I
+ 2I
+ 2I
= 1 . Отсюда
I
=
(7)
Из (6) и (7) находим
I
.
– 0.5I
+
=1 или
– 1.5
I
+
1 – 2.5 I
= 3
Отсюда I
=
–
(А)
Знак
минус у числового значения силы тока
I
свидетельствует
о том, что при произвольном выборе направлений токов, указанных
на
рис.5 , направление тока I
было
указано противоположно истин-
ному.
На самом деле ток I
течет
от узла A
к С.
Ответ: I
= –
A.
Пример 11. Сколько витков нихромовой проволоки диаметром d = 1мм надо навить
на фарфоровый цилиндр радиусом а = 2,5 см , чтобы получить печь сопротивле-
нием R= 40 Ом?
Дано: d = 1мм; а = 2,5 см; R= 40 Ом.
Определить N.
Решение.Сопротивление
проводника можно рассчитать по формуле
- (I),
где
— удельное сопротивление (для нихрома
= 1мк0м.м),
l
— длина
проводника. S
— площадь его поперечного сечения .
Длина
одного витка равна 2
,
тогда длина всей проволоки
l=
N 2
—
(2),
где N — количество витков. Площадь поперечного сечения
_____ (3).
Подставив (3) и (2) в (I), получим
откуда
;
Проверим единицы измеренияй:
.
N единиц измерений не имеет.
Подставив числовые значения и вычисляя, получим:
=200
Ответ N =200.
Пример 12.Реостат из железной проволоки , амперметр и генератор включены последо-вательно. При t0 =00С сопротивление реостата R0= 120 Ом, сопротивление амперметра RAO=20 Ом. Амперметр показывает ток I0 =22 мА. Какой ток будет показывать ампер-
метр,
если реостат нагреется на
T
=50 К.Температурный
коэфициент сопротивления
железа α=6.10-3К-1?
Дано:
t0
=00С
; R0=
120 Ом ; RAO=20
Ом; I0
=22 мА ;
T
=50 К; α=6.10-3К-1.
Определить I.
Решение. Запишем закон Ома для первоначального состояния цепи:
-
(1).
После нагревания реостата его сопротивление R0 изменилось и стало R.Амперметр стал
показывать ток
-
(2).
Сопротивление реостата можно найти по формуле
-
(3).
Удельное сопротивление зависит от температуры следующим образом:
-
(4).
В первоначальном состоянии
,
Откуда
-
(5).
Подставив (4) и (5) в (3),получим
-
(6).
Из (1) найдем
-
(7).
Подставляя (6) и (7) в (2), найдем
.
Подставив числовые значения и вычисляя, получим:
=17,5.10-3(А).
Ответ I= 17,5.10-3(А).