
Физика_вся-10506-yrVar
.pdf
ПРИМЕРЫ И ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ ПО РАЗДЕЛАМ ФИЗИКИ
4.1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
4.1.1. Примеры решения задач Пример 1. Тело вращается вокруг неподвижной оси по закону, выра-
жаемому формулой
j = 10 + 20t – 2t2.
Найти по значению и по направлению полное ускорениеа точки, находящейся на расстоянии 0,1 м от оси вращения, для момента времени t = 4 с.
Решение.
Точка вращающегося тела описывает окружность. Полное ускорение а точки, движущейся по кривой линии, может быть найдено как геометриче-
r
ская сумма тангенциального ускоренияат , направленного по касательной к
r
траектории, и нормального ускорения ан , направленного к центру кривизны траектории:
а = |
ат2 + aн2 . |
(4.1) |
Тангенциальное и нормальное ускорения точки вращающегося тела вы- |
||
ражаются формулами: |
|
|
aT |
= e × r ; |
(4.2) |
aH = w2 × r , |
(4.3) |
|
где w – угловая скорость тела; e – его угловое ускорение; r – расстояние точки от оси вращения.
Подставляя выражения aт и aн в формулу (1), находим: |
|
a = e2r 2 + w4r 2 = r e2 + w4 . |
(4.4) |
Угловая скорость w вращающегося тела равна первой производной от угла поворота по времени:
w = dj = 20 - 4t . dt
В момент времени t = 4 с угловая скорость
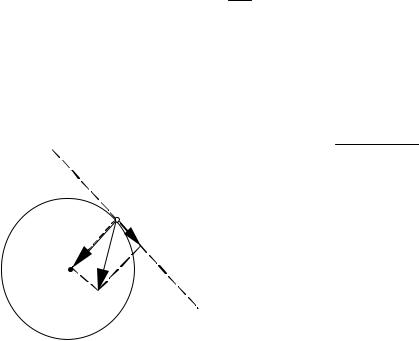
w = (20 – 4×4) = 4 с–1.
Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени:
e = dw = - 4 с-1. dt
Это выражение углового ускорения не содержит времени, следовательно, угловое ускорение имеет постоянное значение, не зависящее от времени.
Подставив найденные значения w и e и заданное значениеr в формулу (4), получим:
|
r |
r |
ат |
ан |
|
а = 0,1 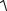
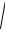 (-4)2 + 44 м/с2 =1,65 м/с2 .
(-4)2 + 44 м/с2 =1,65 м/с2 .
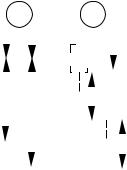
Направление полного ускорения можно определить, если найти углы, которые вектор ускорения образует с касательной к траектории или с нормалью к (рисней.1):
a |
r r |
aт |
|
|
|
|
|
|
|
|
|
cos(a, aт ) = |
|
|
; |
|
|
|
|
|
(4.5) |
|
|
a |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
r r |
|
aн |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
cos(a, aн ) = |
|
|
|
|
; |
(4.6) |
|||
|
|
|
a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
По формулам (2) и (3) найдем значения ат и aн:
ат = – 4 × 0,1 = –0,4 м/с2;
ан = 42 × 0,1 = 1,6 м/с2;
Подставим эти значения и значение полного ускорения в формулы(5) и
(6):
r |
r |
0,4 |
|
|
|
||
cos(a, aт ) = |
|
|
|
|
= 0,242; |
||
|
|
|
|
||||
|
1,65 |
|
|
|
|||
r |
r |
1,6 |
|
|
= 0,97 . |
||
cos(a, aн ) = |
|
|
|
|
|||
1,65 |
|
||||||
|
|
|
|
|
|||
Найдем значения искомых углов: |
|
|
|
|
|
||
r r |
= 76o ; |
|
r r |
|
|||
(a, aт ) |
|
(a, aн ) = 14o . |
|||||
2
Пример 2. Через блок, выполненный в виде диска и имеющий массу m = 80 г (рис. 2), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m1 = 100 г и m2 = 200 г. С каким ускорением будут дви-
гаться грузы, если их предоставить самим себе? (Трением пренебречь.) Р е ш е н и е.
П е р в ы й с п о с о б. Применим к решению задачи основные законы поступательного и вращательного движений. На каждый из движущихся грузов действует две силы: сила тяжести P = mg, направленная вниз, и сила натяжения нити Т, направленная вверх (рис. 2, а). Груз m1 поднимается уско-
ренно вверх, следовательно, T1 > m1g. По второму закону Ньютона равно-
действующая этих сил, равная их разности, прямо пропорциональна массе груза и ускорению, с которым он движется, т. е.
T1 – m1g = m1a,
откуда |
|
|
|
Т1=m1g + m1a. |
(7) |
Груз m2 |
ускоренно опускается вниз, следова- |
|
тельно, T2 < |
m2g. Груз m2 ускоренно |
опускается |
вниз, следовательно, T2 < m2g. Запишем |
формулу |
|
второго закона Ньютона для этого груза: |
|
|
|
m2g – Т2 = m2a, |
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Т1' |
|
m |
|
Т2' |
|
|
|
|
m |
|
a |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
T1 |
|
|
|
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
m2 |
||
m |
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
m1g |
|
|
|
|
|
|
|
||||||||||||
|
|
а |
|
б |
|
|
|
|
||||||||||||||
Рис. 2
Т2 = m2g – m2a. |
(8) |
|
|
|
Согласно основному закону динамики вращательного движения, вра- |
||||
щающий момент М, приложенный к диску, |
равен произведению |
момента |
||
инерции J диска на его угловое ускорение e: |
|
|
|
|
M = Je. |
|
|
(9) |
|
Определим вращающий момент. Силы натяжения нитей действуют не |
||||
только на грузы, но и на диск. По третьему закону Ньютона силыТ |
1 |
¢ и Т |
¢, |
|
|
|
|
2 |
|
приложенные к ободу диска, по своему значению равны, соответственно, си-
3

лам Т1 и Т2, но по направлению им противоположны. При движении грузов диск ускоренно вращается по часовой стрелке, следовательно, Т2¢ > Т1¢. Вра-
щающий момент, приложенный к диску, равен произведению разности этих сил на плечо, равное радиусу диска, т. е.
М = (Т2¢ – Т1¢)r.
Момент инерции диска J = mr 2 ; угловое ускорение связано с линейным
2
ускорением грузов соотношением e = а . Подставив в формулу (9) выражения r
для M, J и e, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Т |
¢ – Т |
¢)r = |
mr 2 |
|
а |
. |
|
|
|
(10) |
|||||
|
|
|
|||||||||||||
2 |
|
|
1 |
|
|
2 |
|
|
r |
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
Из выражения (10), ползуясь формулами (7) и (8), получим: |
|
||||||||||||||
m2g – m2a – m1g – m1a = |
m |
a |
|
||||||||||||
|
|
|
|||||||||||||
или |
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(m2 – m1)g=(m2 + m1 |
+ |
m |
)a , |
|
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
|
m2 - m1 |
|
g. |
(11) |
||||||||||
m |
|
+ m + m |
|||||||||||||
|
|
|
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отношение масс в правой части формулы(11) есть величина безразмерная. Поэтому числовые значения масс m1, m2 и m можно взять в граммах, как они и даны в условии задачи. Числовое значение ускорения g надо взять в единицах СИ. После подстановки получим:
а = |
200 |
-100 |
|
|
× 9,81 = 2,88 м с2 . |
200 + 100 + |
80 |
|
|||
|
|
|
|||
|
2 |
|
|
||
|
|
|
|
|
|
В т о р о й с п о с о б. Применим к решению задачи закон сохранения энергии, согласно которому при отсутствии трения полная энергия изолиро-
4

ванной системы тел остаётся неизменной во времени при движении этих тел; энергия при этом превращается из потенциальной в кинетическую, и наоборот. Напомним, что в механике полной энергией тела называется сумма его потенциальной и кинетической энергий.
Положим, что в начальный момент движения потенциальная энергия первого груза была равна Eп1 , второго – Eп2 . Через некоторое время высота
первого груза увеличилась наh, второго – уменьшилась на h (рис. 2, б). Потенциальная энергия первого груза стала равнаEп2 + m1gh, второго: Eп2 –
– m2gh. Кроме того, каждый из грузов, двигаясь с ускорением а, приобрел за это время скоростьυ и кинетическую энергию, равную, соответственно,
m1х 2 .
2
Точно так же диск, вращаясь равноускоренно, приобрел угловую ско-
рость w и соответствующую ей кинетическую энергию |
|
Jw2 |
|
. |
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем выражение кинетической энергии диска. Поскольку |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
J = |
mr 2 |
|
|
и w = |
х |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то |
1 |
J щ= |
|
1 mr 2 х2 |
= |
|
mх |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
2 |
|
2 r 2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
По закону сохранения энергии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m х2 |
|
|
m |
2 |
х2 |
mх |
4 |
|
|
|||
|
|
Eп |
+ Eп |
2 |
= |
Eп |
+ m1gh + |
Eп |
2 |
– m2gh + |
1 |
|
+ |
|
|
+ |
|
|
. |
(12) |
|||||||||||||
|
|
|
|
2 |
4 |
|
|||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
Перенесем члены, соответствующие потенциальной энергии грузов, из правой части равенства (12) в левую. После очевидных преобразований получим:
(m2 - m1 )gh = (m2 + m1 + m) х2 . 2 2
Так как грузы двигались равноускоренно, то u2 = 2ah. Следовательно,
5

(m |
2 |
- m )g = (m |
2 |
+ m + |
m |
)а , |
||||||
|
||||||||||||
|
1 |
|
|
|
1 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а = |
|
m2 - m1 |
|
|
||||||
|
|
|
|
|
|
|
g, |
|
|
|||
|
|
m |
2 |
+ m + |
m |
|
|
|
||||
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
т. е. получено выражение совпадающее с выражением (12).
Пример 3*. Два маховика, выполненные в виде дисков радиусами 0,4 м и имеющие массу100 кг каждый, были раскручены до скорости вращения 480 об/мин и затем предоставлены сами себе. Под действием трения валов о подшипники первый маховик остановился через1 мин 20 с; второй маховик до полной остановки сделал240 об. Определить моменты сил трения вала о подшипники у каждого маховика и сравнить эти силы между собой.
Р е ш е н и е.
Найдем момент сил трения, действующий на первый маховик. Для этого воспользуемся основным уравнением динамики вращательного движения в виде
М1Dt = Jw2 - Jw1,
где М1 – вращающий момент (в данном случае – искомый момент силы тре-
ния); Dt – время действия вращающего момента; J – момент инерции махови-
ка; w1 – начальная угловая скорость вращения маховика; w2 – его конечная угловая скорость.
Решив это уравнение относительно М1, получим:
М1 = J (w2 - w1) .
Dt
Найдем числовые значения величин J и w1 и подставим их в выражение для М1:
6

J = |
mr 2 |
= |
100 × (0,4)2 |
= 8 кг× м 2 ; |
|
|
|||
2 |
2 |
|
||
w1 = 2 × 3,14 × 480 = 50 с-1; 60
Dt =1 мин 20 с = 80 с,
М1 = 8 × (0 - 50) = -5 Н× м . 80
(Знак ²минус² означает, что момент М1 – тормозящий.)
Найдем момент сил трения, действующих на второй маховик. Так как в условии задачи дано число оборотов, сделанных вторым маховиком до полной остановки, то воспользуемся уравнением, выражающим связь между работой и изменением кинетической энергии для вращательного движения:
М 2Dj = Jщ22 - Jw12 , |
|
2 |
2 |
где Dj – угол поворота тела.
Решив это уравнение относительно М2, получим:
|
|
J (w2 |
- w2 ) |
|
М 2 |
= |
2 |
1 |
. |
|
|
|||
|
|
2Dj |
||
В полученное для М2 выражение подставим числовые значения входя-
щих величин и произведем вычисления:
J= 8 кг×м2; w2 = 0;
w1 = 50 с –1;
j = 2pN = 2p×240 = 1507 рад;
М 2 = 8 × (0 - 502 ) = - 6,64 Н× м . 2 ×1507
Чтобы сравнить полученные значения моментов сил трения, найдем отношение их абсолютных значений:
М2 = 6,44 = 1,33.
М1 5
7

У второго маховика момент сил трения больше в 1,33 раза.
Пример 4. С какой скоростью движется Земля вокруг Солнца? (Принять, что Земля движется по круговой орбите.)
Р е ш е н и е.
На тело, движущееся по круговой орбите, действует центростремительная сила, величина которой выражается формулой
Fцс = mх 2 .
R
где m – масса тела; u – скорость движения тела по орбите; R – радиус кривизны орбиты.
В рассматриваемом случае центростремительной силой является сила притяжения Земли Солнцем, которая выражается формулой
|
F = g |
mM |
|
, |
|
|||||
R 2 |
|
|||||||||
|
|
|
|
|
|
|||||
где g – гравитационная постоянная; M |
|
– |
|
масса Солнца; R – расстояние |
||||||
центра Земли от центра Солнца (равно радиусу орбиты). |
||||||||||
Приравняв выражения для центростремительной силыFцс и силы при- |
||||||||||
тяжения F, получим уравнение |
|
|
|
|
|
|
|
|||
|
mх2 |
|
mM |
, |
||||||
|
|
= g |
|
|
|
|
|
|||
|
|
R2 |
|
|||||||
|
R |
|
|
|
||||||
откуда |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
х = |
gМ |
. |
|
|
|||||
|
|
|
|
|||||||
|
|
|
|
|
R |
|
|
|||
Подставим в это выражение числовые значения входящих в него величин:
g= 6,67·10 –11 м3/(кг×с2);
М= 1,98×1030 кг;
R = 1,49×1011 м.
Выполняя арифметические действия, находим:
х = |
6,67 ×10 -11 ×1,98 ×1030 |
= 2,98 ×104 = 29,8 км с . |
|
||
1,49 ×1011 |
|
|
8

Пример 5. С какой скоростью должна быть выброшена с поверхности Солнца частица, чтобы она могла удалиться за приделы солнечной системы?
Р е ш е н и е.
Частица должна быть выброшена с такой скоростьюu, чтобы соответствующая этой скорости кинетическая энергия была равна работеА, совершаемой против сил притяжения частицы к Солнцу при удалении её в беско-
нечность, т. е. чтобы |
mх |
2 |
= A, откуда |
|
||||
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х = |
2 А |
. |
(13) |
||
|
|
|
|
|||||
|
|
|
|
|
m |
|
||
Для того чтобы вычислить работу, совершаемую против силы притяжения F при удалении тела от Солнца, используем правило нахождения работы переменной силы. Элементарная работа против силы притяженияF при удалении на расстояние dr выразится так:
dA = Fdr = g mM dr, r 2
где m – масса тела; M – масса Солнца; r – расстояние тела от Солнца.
Работа, которую нужно совершить, чтобы удалить тело с поверхности Солнца в бесконечность, будет равна:
¥ |
dr |
¥ dr |
|
M |
|
||
A = ò gmM |
|
= gmM ò |
|
|
= gm |
|
, |
r 2 |
|
2 |
R |
||||
R |
R r |
|
|
||||
где R – радиус Солнца.
Подставим полученное выражение работы А в формулу (13):
х = 2gМ
R
и вычислим это значение скорости:
g= 6,67·10 – 11 м3/(кг×с2);
М= 1,98×1030 кг;
|
|
R = 6,95×108 м; |
|
||
х = |
|
2 × 6,67 ×10-11 ×1,98 ×1030 |
|
= 6,15 ×105 |
= 615 км с . |
|
|||||
6,95 ×108 |
|
|
|
||
9
Пример 6. Материальная точка с массой0,01 кг совершает гармонические колебания с периодом2 с. Полная энергия колеблющейся точки равна
10–4 Дж.
1.Найти амплитуду колебаний. 2. Написать уравнение данных колебаний. 3. Найти наибольшее значение силы, действующей на точку.
Ре ш е н и е.
1.Запишем уравнение гармонических колебаний в виде
x = A sin w t.
Взяв первую производную смещениях по времени, найдем скорость колеблющейся точки:
|
х = |
dx |
= Aщ cos щt . |
|
(14) |
|||||
|
|
|
|
|||||||
|
|
|
dt |
|
|
|
|
|
|
|
Воспользовавшись равенством (14), |
получим для |
кинетической энергии |
||||||||
колеблющейся точки |
|
|
|
|
|
|
|
|
|
|
Eк = |
|
mх 2 |
|
= |
mA |
2 w2 cos 2 wt |
. |
|
||
2 |
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|||
Полная энергия колеблющейся точки равна максимальному значению кинетической энергии точки:
Eк max |
|
|
|
mA2w2 |
|||||
= |
|
|
|
. |
|||||
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Отсюда находим следующее выражение для амплитуды колебаний; |
|||||||||
|
|
|
|
|
|
|
|
||
A = |
1 |
|
|
|
2Aк max |
. |
|||
w |
|
||||||||
|
|
|
|
m |
|||||
Циклическая частота w связана |
с |
периодом колебанийt соотношением |
|||||||
w = 2p . t
Подставим это соотношение в предыдущее выражение:
А = |
t |
|
2Eк max |
2p |
|
m |
|
|
|
и произведем вычисления:
10
