МЧС России

Санкт-Петербургский университет государственной противопожарной службы

Утверждаю

Начальник кафедры физики и теплотехники, полковник вн.сл. Иванов А.Н.

(должность, звание, ФИО)

«13» октября 2008 года

ЛЕКЦИЯ

по учебной дисциплине «Физика»

Специальность 280104.65 - Пожарная безопасность

Заочное отделение, 6 лет

Тема № 7 «Основы молекулярной физики и термодинамики»

Обсуждена на заседании кафедры

Протокол № 2/10 от

«13» октября 2008 года

Санкт- Петербург

2008

I. Цели занятия

1. Образовательная – изучение понятий и законов раздела основы молекулярной физики и термодинамики

2. воспитательные

- применение рассмотренных явлений в пожарной безопасности

- повышение квалификации сотрудников ГПС

II. Расчёт учебного времени

Содержание и порядок проведения занятия	Время, мин.
ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы 1. Основное уравнение молекулярно-кинетической теории идеального газа. 2. Термодинамика идеального газа ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ	5 170 80 90 5

III. Литература

Основная:

1. Трофимова Т.И. Курс физики. - М.: Высшая школа, 2003, с.81-118.

Дополнительная:

Савельев И.В. Курс общей физики. - М.: Наука, 1989, Т.1.

Трубилко А.И., Звонов В.С., Поляков А.С., Дятченко А.А. Электричество. Пособие для самостоятельной работы - СПб.: СПбИПБ МВД России, 1998.

IV. Учебно-материальное обеспечение

1. Технические средства обучения: мультимедийный проектор, интерактивная доска.

V. Текст лекции

Вводная часть. Ставятся цели занятия.

Учебные вопросы

1. Основное уравнение молекулярно-кинетической теории идеального газа.

Различают три агрегатных состояния вещества  твердое, жидкое и газообразное. Газообразное состояние является наиболее простым, т. к. в этом случае силы, действующие между молекулами, очень малы, и при определенных условиях ими можно пренебречь. В настоящем курсе молекулярной физики в основном рассматриваются свойства газов. При этом сначала мы будем полагать, что межмолекулярные силы в них не только малы, но и полностью отсутствуют. Пренебрежем также размерами молекул, т. е. будем считать их материальными точками. При таких допущениях молекулы газа должны считаться совершенно свободными. Это означает, что, как и тела, не подверженные действию каких-либо сил, они движутся прямолинейно и равномерно. Следовательно, каждая молекула ведет себя так, как будто других молекул в сосуде нет. Газ, обладающий такими же свойствами, как и совокупность невзаимодействующих материальных точек, называется идеальным газом. Более строго: под идеальным газом понимается система, в которой можно пренебречь энергией взаимодействия частиц (атомов или молекул) по сравнению с их кинетической энергией. В такой системе частицы в основном движутся прямолинейно и равномерно, испытывая кратковременные столкновения друг с другом и со стенками сосуда, в котором газ заключен.

Уравнение, связывающее три величины  давление , объеми температуругаза, для данной его массы называетсяуравнением состояния. В общем виде оно может быть записано следующим образом: . Это значит, что состояние газа определяется только двумя независимыми параметрами (например, давлением и объемом), третий параметр однозначно определяется двумя другими.

Всякий газ, если он достаточно разрежен, подчиняется закону Клапейрона

. (1)

Здесь  масса газа,  молекулярный вес,  универсальная газовая постоянная. Величина

(2)

представляет собой число киломолей в данной массе газа. Если ввести понятие молярного объема . т. е. объема, приходящегося на один киломоль газа

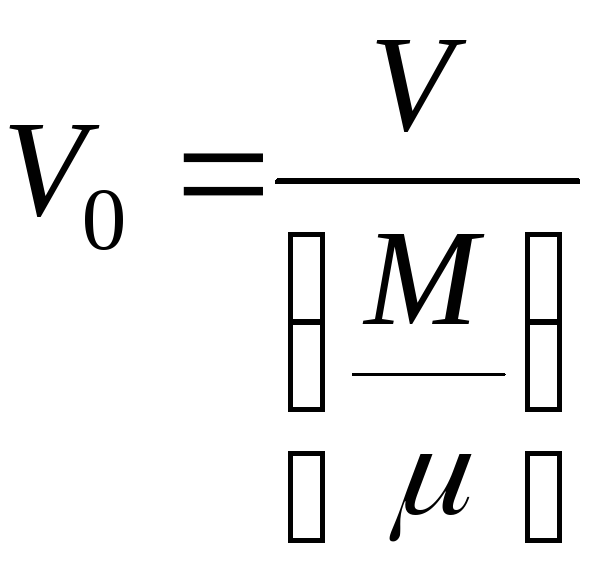, (3)

то уравнение (1.1) примет вид

, (4)

универсальный для всех сортов газов. Уравнение (1) (или (4)) представляет собой уравнение состояния идеального газа.

Единицы измерения:

,

,

,

,

,

.

Отсюда вытекает размерность газовой постоянной: и численное значение в системе единиц СИ:

. (5)

Из (1.4) легко получить как частный случай известные законы идеальных газов.

1) Закон Бойля  Мариотта

При .

. (6)

Это – изотермы При малых объемах газ в действительности перестает быть идеальным.

2) Закон Гей-Люссака  Шарля

При .

(7)

Это – изобары. График изобары имеет вид прямой, исходящей из начала координат

3) Закон Гей-Люссака

При .

(8)

Процесс, происходящий при постоянном объеме, называется изохорическим. График изохоры, как и график изобары, представляет собой прямую, исходящую из начала координат

2. Термодинамика идеального газа

Изменение состояния и работа.Возьмем какое-либо физическое тело. Будем называть его системой. С точки зрения физики система характеризуется своим состоянием. Состояние характеризуется совокупностьюпараметров (внешних и внутренних).

Всякая система, поставленная в определенные внешние условия, рано или поздно приходит в состояние термодинамического (статистического) равновесия.Это утверждение можно рассматривать как один из основных постулатов статистической физики.

В понятие определенных внешних условий входит, во-первых, задание положений (координат) внешних по отношению к системе тел, определяющих силы, действующие на частицы системы. Эти координаты (положения) внешних тел называются внешними параметрами.В случае однородной изотропной системы вместо задания координат стенок сосуда, внутри которого заключена система, в качестве внешнего параметра можно ввести просто объем системы. В тех случаях, когда внешние тела создают в системе протяженные полямагнитные, электрические, гравитационные,в качестве внешних параметров выбираются напряженности самих полей.

Наряду с внешними параметрами будем различать внутренние параметрывеличины, характеризующие свойства самой системы. Например, к их числу относится давление, которое для однородной и изотропной системы при отсутствии внешних полей зависит от объема и температуры (или энергии) системы. К числу внутренних же параметров принадлежит степень диссоциации молекулярного газа, зависящая от его плотности (объема) и температуры. Вообще говоря, внутренние параметры зависят от внешних параметров и температуры (или энергии) системы.

В состоянии термодинамического равновесия системы ее внутренние параметры имеют, при заданных внешних параметрах и температуре (энергии),определенные численные значения(с точностью до малых флуктуаций, обусловленных молекулярной структурой системы).

Рассмотрим простейшую систему идеальный газ. Если считать массу газа заранее заданной, например,, то параметрами, характеризующими состояние этой системы, будут давление, объеми температура. Они связаны уравнением состояния идеального газа (1.4): . Таким образом, независимыми будут любые два из них. Варьируя параметры можно приводить систему в разные состояния.

1.Опыты Джоуля показали, что при переходе механической работы в тепло 1) одинаковое количество работывсегдадает одинаковое количество тепла; 2) тепло пропорционально работе.

4,184 дж1калория, (9)

где 1 калорияколичество тепла, нагревающего 1гводы в интервале температур отдо.

Замечание:количество тепла измеряется при этом исходя из формулы:.

2.Если мы будем переводить систему (газ) из состояния 1 в 2 и учитывать при этом не только работу (зависящую от пути перехода), но и переданное тепло (тоже зависящее от пути перехода), то в сумме совершенная над газом работа и сообщенное ему тепло не зависят от пути перехода. Значит, их сумма является функцией, зависящей только от состояний 1 и 2.Этаоднозначнаяфункция состояниявнутренняя энергия системы

Отсюда мы приходим к первому началу термодинамики, которое является обобщением закона сохранения механической энергии: при любых возможных способах перехода из состояния 1 в 2 сумма механических эквивалентов всех внешних воздействий остается неизменной.

В дифференциальной форме:

, (10)

здесь работа, совершаемая внешними силами над газом, а- теплота, сообщаемая газу.

Таким образом, при феноменологическом развитии термодинамики 1-ое начало постулируетдля системы существование некоторой функции состояния, называемой внутренней энергией, которая может меняться как за счет работы, совершаемой над системой, так и за счет теплоты, ей передаваемой .