
- •Глава 2 предел функции
- •2.1. Определение предела функции
- •2.2. Односторонние пределы
- •2.3. Условие существования предела функции
- •2.4. Предел функции при бесконечно большом значении аргумента ()
- •2.5. Предел числовой последовательности
- •2.6. Бесконечно большие функции
- •2.7. Бесконечно малые функции
- •2.8. Связь между функцией, ее пределом и бесконечно малой функцией
- •2.9. Основные теоремы о пределах
- •2.10. Признак существования предела функции
- •2.11. Два замечательных предела
- •Первый замечательный предел
- •Второй замечательный предел
- •2.12. Эквивалентные бесконечно малые
- •2.13. Вычисление пределов функций. Раскрытие неопределенностей
- •Примеры
- •Неопределенность вида
- •Примеры
- •Примеры
2.9. Основные теоремы о пределах
Приведем без доказательства теоремы, которые облегчают нахождение пределов функций.
Пусть
![]() и
и![]() − функции, для которых существуют
пределы при
− функции, для которых существуют
пределы при![]() (или
(или![]() ),
т.е.
),
т.е. и
и .
.
Теорема.
Если функция
![]() постоянна, то ее предел равен ей самой:
постоянна, то ее предел равен ей самой:
 .
.
Теорема.
Предел суммы (разности) двух функций равен сумме (разности) их пределов:
 .
.
Следствие.
Функция может
иметь только один предел при
![]() .
.
Теорема.
Предел произведения двух функций равен произведению их пределов:
 .
.
Следствие.
Постоянный множитель можно выносить за знак предела:
 .
.
Следствие.
Предел степени с натуральным показателем равен той же степени предела:
 .
.
Теорема.
Если предел функции
![]() отличен от нуля, то предел обратной ей
по величине функции
отличен от нуля, то предел обратной ей
по величине функции![]() равен обратной величине предела данной
функции:
равен обратной величине предела данной
функции:
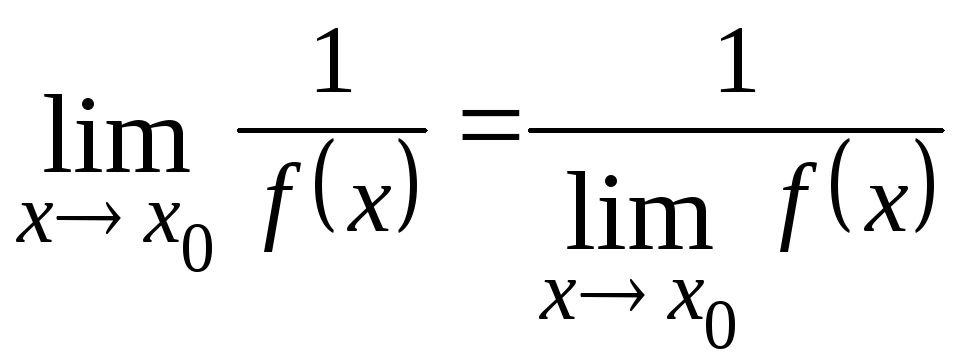 .
.
Теорема.
Предел частного равен частному пределов, если предел знаменателя отличен от нуля:
 .
.
Теорема.
Если для функции
![]() существует
существует![]() ,
то
,
то
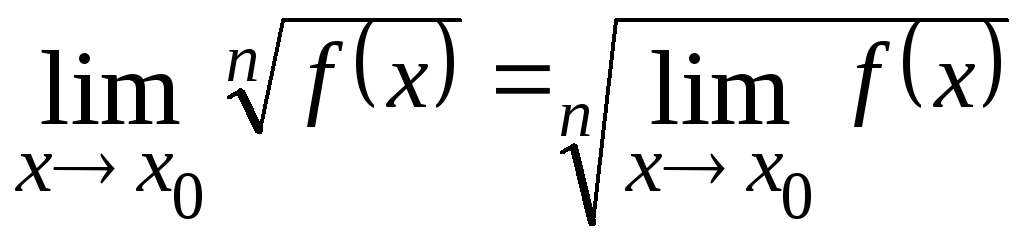 .
.
2.10. Признак существования предела функции
Не всякая функция
имеет предел, даже будучи ограниченной.
Например,
![]() при
при![]() предела не имеет, хотя
предела не имеет, хотя![]() .
.
При решении некоторых задач бывает достаточно только убедиться в существовании предела функции, а числовое значение предела при этом имеет второстепенную роль. В таких случаях пользуются признаками существования предела.
Укажем такой признак.
Теорема.
Если функция
![]() заключена между двумя функциями
заключена между двумя функциями![]() и
и![]() ,
стремящимися к одному и тому же пределу,
то она также стремится к этому пределу,
т.е. если
,
стремящимися к одному и тому же пределу,
то она также стремится к этому пределу,
т.е. если
![]()
![]() ,
,
 ,
, ,
,
то
 .
.
2.11. Два замечательных предела
Замечательными (вследствие большого числа их приложений) в математике называются пределы двух следующих функций, когда их аргумент х стремится к нулю:
![]() и
и
![]() .
.
Первый замечательный предел
Теорема.
Предел отношения синуса бесконечно малого угла к величине этого угла в радианах равен единице:
 .
.
Это равенство указывает на тот факт, что при очень «небольших» значениях х
![]() .
.
Первый замечательный предел часто используют при вычислении пределов выражений, содержащих тригонометрические функции.
Второй замечательный предел
Можно доказать, что функция
![]()
при
![]() стремится к числуе:
стремится к числуе:
 .
.
Число е
иррациональное, его приближенное
значение равно 2,72 (![]() …).
Числое
служит основанием натуральных логарифмов
(
…).
Числое
служит основанием натуральных логарифмов
(![]() )
и играет важную роль в математике.
)
и играет важную роль в математике.
Дадим другое
выражение для числа е.
Полагая
![]() (
(![]() ,
т.к.
,
т.к.![]() ),
будем иметь
),
будем иметь
 .
.
Оба равенства называют вторым замечательным пределом. С помощью числа е удобно выражать многие пределы.
Замечание.
Показательная функция вида
![]()
называется экспоненциальной, употребляется также обозначение
![]() .
.
2.12. Эквивалентные бесконечно малые
Пусть
![]() и
и![]() − бесконечно малые функции при
− бесконечно малые функции при![]() (или
(или![]() ),
т.е.
),
т.е. и
и .
.
Если
 ,
то
,
то![]() и
и![]() называютсяэквивалентными
бесконечно малыми (при
называютсяэквивалентными
бесконечно малыми (при
![]() ).
).
Обозначается: ![]() .
.
Например,
![]() при
при![]() ,
т.к.
,
т.к. .
.
Для эквивалентных бесконечно малых справедливы следующие свойства:
Если
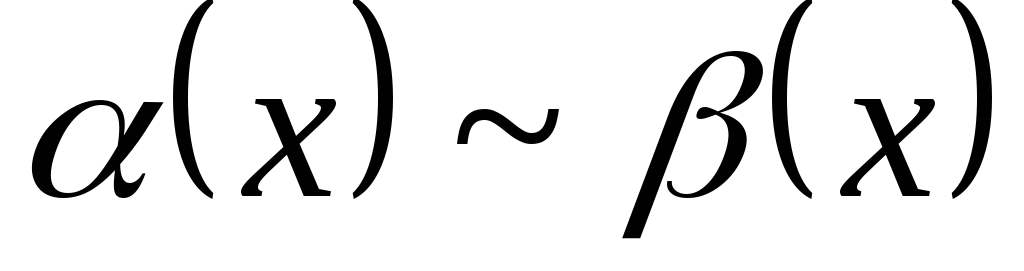 при
при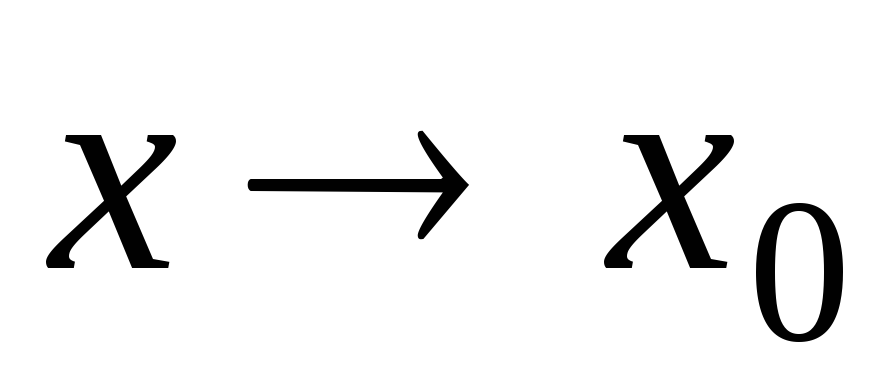 ,
то
,
то .
.Если
 и
и при
при ,
то
,
то при
при .
.Если
 и
и при
при ,
то
,
то ,
т.е. предел отношения двух бесконечно
малых величин равен пределу отношения
эквивалентных им бесконечно малых.
,
т.е. предел отношения двух бесконечно
малых величин равен пределу отношения
эквивалентных им бесконечно малых.
Последнее свойство означает, что при нахождении предела, можно бесконечно малые, стоящие в числителе или в знаменателе или в обоих, заменять эквивалентными им величинами, в частности, более простыми. Такой прием часто применяют при вычислении пределов функций.
Ниже приведены важнейшие эквивалентности, которыми пользуются при вычислении пределов функций:
|
1. |
|
при
|
|
2. |
| |
|
3. |
| |
|
4. |
| |
|
5. |
| |
|
6. |
| |
|
7. |
| |
|
8. |
| |
|
9. |
|

