1.2. Понятие функции

Для исследования различных явлений полезно знать, как изменение одних величин влияет на другие величины.

Понятие функции связано с установлением зависимости (связи) между двумя (несколькими) переменными величинами при их совместном изменении, или установлением зависимости между элементами двух (нескольких) множеств.

Определение.

Пусть даны две переменные х и y с областями изменения Х и Y. Переменная y называется функцией от х, если по некоторому правилу или закону каждому значению ставится в соответствие одно определенное значение.

Для указания этого факта, что y есть функция от х, пишут: ,,и т.п.

Можно также сказать, что функция f отображает множество Х на множество Y. Это обозначается так (рис.1.1).

Рис. 1.1

Переменная х называется независимой переменной или аргументом.

Переменная y называется зависимой переменной или функцией.

Относительно самих величин х и y говорят, что они находятся в функциональной зависимости.

1.3. Область определения и изменения функции

Определение.

Совокупность всех значений независимой переменной х, для которых функция y определена, называется областью определения или областью существования этой функции.

Определение.

Множество Х называется областью определения функции и обозначается .

Обычно областью определения функции являются:

• отрезок (сегмент или замкнутый промежуток)

;

• интервал (открытый промежуток)

;

• полуоткрытые интервалы (полуоткрытые отрезки)

;

;

• бесконечные интервалы (промежутки)

; ;

; ;

,

где ,и.

Например, для функций:

1) ;

2) .

Область определения функции может состоять из одного или нескольких промежутков и из отдельных точек.

Определение.

Множество значений Y называется областью изменения или областью значений функции, и обозначается .

Область изменения функции (множество ее значений) определяется законом соответствия.

Например, для функций

1) ;;

2) ;.

Определение.

Функция называетсячисловой функцией, если ее область определения и множество значенийсодержатся в множестве действительных чиселR.

В дальнейшем будем изучать лишь числовые функции. Частное значение функции призаписывается так:.

Например, если , то,,и т.п.

1.4. Последовательность

Определение.

Функция, определенная на множестве натуральных чисел , называетсяпоследовательностью.

Значения функции т.е. элементы множестваназываются членами последовательности, а– общим членом последовательности.

Последовательность обычно обозначают через или.

Например, ;.

1.5. График функции

Для наглядного представления функции строят ее график.

Определение.

Графиком функции называется множество всех точек плоскости, для каждой из которыхх является значением аргумента, а y – соответствующим значением функции.

Например, графиком функции является верхняя полуокружность радиусас центром в(рис. 1.2).

Рис. 1.2

1.6. Способы задания функции

Задать функцию – это значит указать правило, позволяющее по данному значению независимой переменной находить соответствующее значение функции.

Существует три основных способа задания функции: аналитический, табличный и графический.

Аналитический способ состоит в том, что зависимость между переменными величинами задается в виде формулы (аналитического выражения), указывающей, какие и в каком порядке действия надо выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.

Например, ;;, где.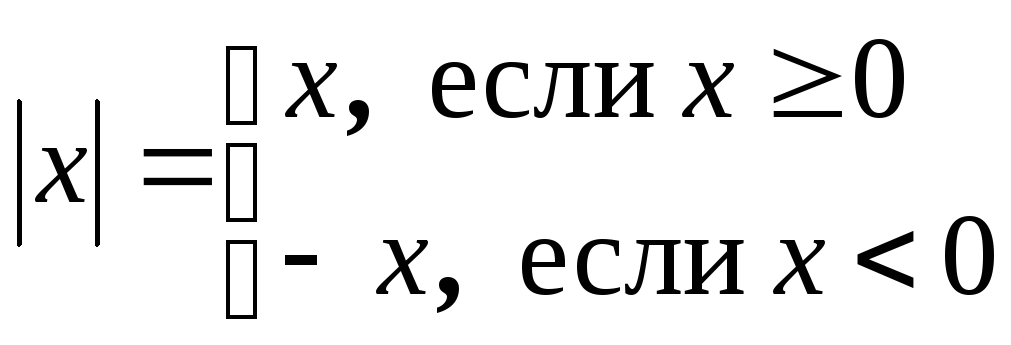

Аналитический способ является наиболее совершенным, т.к. к нему могут быть применены методы математического анализа, позволяющие полностью исследовать функцию.

Табличный способпредусматривает задание таблицы, в которой различным значениям аргументапоставлены соответствующие значения функции:

х	х1	х2	…	хn
y	y1	y2	…	yn

Такие таблицы составляются, например, по данным эксперимента; для облегчения вычислений с часто встречающимися функциями (таблицы логарифмов, таблицы тригонометрических функций и т.д.).

Графический способзадания функции состоит в том, что в данной системе координат задается некоторая кривая. Преимуществом графического задания является его наглядность, недостатком – его неточность.