
Ефимова, Корычев Теплотехника-2012
.pdf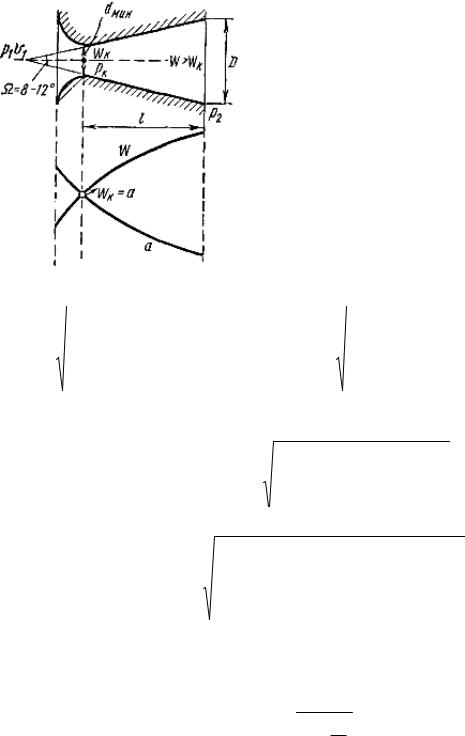
11.6. Истечение идеального газа из комбинированного сопла Лаваля
Комбинированное сопло Лаваля предназначено для использования больших перепадов давления и для получения скоростей истечения, превышающих критическую или скорость звука. Сопло Лаваля состоит из короткого суживающегося участка и расширяющейся конической насадки (рис. 33).
|
|
|
|
|
|
|
|
|
|
|
Опыты показывают, что угол конусно- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
сти расширяющейся части должен быть ра- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
вен Ω = 8–12°. При больших углах наблюда- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ется отрыв струи от стенок канала. При исте- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
чении газа из комбинированного сопла в ок- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ружающую среду с давлением меньше кри- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
тического в самом узком сечении сопла ус- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
танавливается критическое давление рк и |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
критическая скорость ωк. В расширяющейся |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
насадке сопла происходит дальнейшее уве- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
личение скорости газа и падение давления до |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
давления внешней среды. Скорость истече- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ния и секундный расход идеального газа (при |
||||||||||||||||
Рис. 33. Сопло Лаваля |
|
|
|
|
заданном а) определяются по формулам |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
k 1 |
|
|
|
|
k |
|
|
p |
2 |
k |
|
|
|
k |
p |
|
p |
|
k |
|
p |
|
k |
|
||||||
|
2 |
|
p1υ1 |
1 |
|
|
|
|
и m a 2 |
|
|
1 |
|
|
2 |
|
|
|
2 |
|
. |
||||||
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
k 1 |
|
|
|
|
|
k 1 |
υ1 |
p1 |
|
p1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При заданном расходе площадь минимального сечения сопла аmin можно вычислить по формуле
|
|
k |
|
p1 |
|
|
|
2 |
|
|
|
|
|
|
2 k 1 |
|
|||||||
mmax amin |
|
|
|
||||||||
2 |
|
|
|
|
|
, |
|||||
|
|
|
|
|
|||||||
|
k 1 |
υ1 |
k 1 |
|
|||||||
а площадь выходного сечения сопла а – по формуле
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
k 1 |
|
k |
|
|
p |
|
|
p |
|
k |
|
|
p |
|
|
k |
|
||
|
|
|
2 |
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
m a 2 |
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
p1 |
|
|
||||||||
k 1 |
υ1 |
p1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Длина суживающейся части обычно берется равной диаметру выходного сечения сопла. Длину расширяющейся насадки l (рис. 33) можно определить по уравнению
l D d , 2tg
2
где D – диаметр выходного отверстия; d – диаметр сопла в минимальном сечении; – угол конусности сопла.
81

Контрольные вопросы
1.Написать уравнение первого закона термодинамики для потока.
2.Объяснить все величины, входящие в уравнение для потока.
3.Какие каналы называются соплами и диффузорами?
4.Какое состояние называется стационарным?
5.Написать уравнение неразрывности для потока.
6.Вывод уравнения работы проталкивания.
7.Уравнение первого закона термодинамики для потока с применением энтальпии.
8.Вследствие чего происходит изменение внешней кинетической энергии рабочего тела при адиабатном процессе истечения?
9.Какая величина называется располагаемой работой?
10.Графическое изображение располагаемой работы в р,υ-диаграмме.
11.Уравнение располагаемой работы для политропного и адиабатного процессов.
12.Уравнение располагаемой работы при адиабатном процессе с применением энтальпии.
13.Скорость истечения жидкости при адиабатном процессе.
14.Скорость истечения идеального газа при адиабатном процессе.
15.Массовый расход идеального газа.
16.Основные условия течения по каналам переменного сечения.
17.Дать описание комбинированного сопла Лаваля.
18.Как определяется скорость истечения и массовый расход газа при выходе из сопла Лаваля?
19.Как определяются площади минимального и выходного сечений сопла Лаваля?
20.Как определяется длина сопла Лаваля?
Задача
Из комбинированного сопла газовой турбины вытекают продукты сгора-
ния при давлении р = 1,3∙105 Па. |
При входе в сопло давление газов равно |
р1 =10,0∙105 Па при температуре |
1200 К (927 ºС). Массовый расход газов |
m = 0,8 кг/с. Истечение считать адиабатным, а показатель k = ср/сυ =1,35. Продукты сгорания обладают свойствами воздуха. Трением в канале сопла и входной скоростью пренебречь. Определить минимальное и входное сечения сопла, а также температуру газов при выходе из сопла.
Решение
Определим критическое отношение давлений по данным задачи.
|
|
|
p |
|
2 |
|
k |
2 |
|
|
|
1,35 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1,35 1 |
|
|
|
|
|
||||||||||
|
|
|
|
k 1 |
0,537. |
|
||||||||||||||||
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||||
p1 |
|
|
|
|
||||||||||||||||||
|
|
k 1 |
|
1,35 1 |
|
pk |
|
|
|
|
||||||||||||
Для нашей задачи отношение давлений |
k |
|
|
1,3 |
0,13 k |
0,5367. |
||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Следовательно, обязательно надо применить комбинированное сопло Лаваля. Определим скорость газов в критическом сечении сопла:
|
|
|
2 |
k |
p υ |
|
|
2 |
2 |
RT |
|
2 |
1,35 |
|
287 1200 629 |
м |
. |
||
|
|
|
|
|
|
||||||||||||||
|
k |
|
|
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
с |
|
|
|
|
k 1 |
|
|
|
k 1 |
|
|
1,35 1 |
|
|
|||||||
Зная критическую скорость и массовый расход газов, можно определить площадь критического сечения сопла (минимальную) – амин:
82

aмин |
mυk |
|
|
0,8 0,546 |
0,000694 м2; |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
k |
629 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
υk |
|
υ1 |
|
|
0,3444 |
|
|
0,546 |
м3 |
, |
|
|
|
||||||||||||||||
1 |
1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
k |
|
|
|
0,537 |
|
|
|
|
|
|
|
|
|
|
кг |
|
|
|
|
||||||
|
|
k |
1,35 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
где υ1 определяем по формуле Клапейрона: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
RT |
|
287 1200 |
|
|
|
|
|
|
м3 |
|||||||||||||||||
υ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0,3444 |
|
|
|
. |
|
|
||||||||
1 |
|
|
p |
|
|
10 102 |
|
|
|
|
|
|
кг |
||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Диаметр критического сечения dk |
|
|
|
aмин |
|
|
|
694 |
|
29,8 мм. |
|||||||||||||||||||
|
|
0,785 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0,785 |
|
|
|
||||||||||||||||
Длину суживающейся части сопла берем равной диаметру критического сечения (из конструктивных соображений) l1 = 30 мм.
Определим скорость газов в выходном сечении сопла:
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
k |
p |
|
p2 |
|
|
2 |
k |
RT |
|
k 1 |
|
|
|
||||||
|
|
|
k |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
В |
|
|
|
|
1 |
k |
|
782м/с |
. |
|||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 1 |
|
p1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
k 1 |
|
|
|
|
k 1 |
|
|
|
|
|
|
|
||||||||
Зная выходную скорость газов, можно определить площадь выходного сечения сопла:
a |
В |
|
mυ2 |
|
0,8 1,524 |
0,001559 м2; |
|
||||||||||||||||
|
|
782 |
|
|
|
||||||||||||||||||
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
υ2 |
υ1 |
|
|
0,3444 |
|
1,524 |
м3 |
. |
|
|
|
|
|||||||||
|
|
1 |
1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
k |
|
|
0,13 |
1,35 |
|
|
|
|
|
|
кг |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
Диаметр выходного сечения сопла D |
aВ |
|
|
1559 |
|
44,6 мм. |
|||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,785 |
0,785 |
|
|||||||
D d
Длину расширяющейся части сопла l2 определим по уравнению l 2tg .
2
Угол конусности насадки принимаем равным 10º, tg 10º = 0,17633, тогда
l2 |
|
44,6 29,8 |
85 мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0,17498 |
|
|
|
|
|
|
|
|
|
|
Длина сопла газовой турбины l l1 l2 30 85 115 мм. |
|||||||
|
|
Температуру газов при выходе из сопла Т2 |
определяем из уравнения Кла- |
||||||
пейрона: |
|
p2υ2 |
|
1,3 105 1,524 |
|
|
|||
|
|
|
T2 |
|
|
|
693 К. |
||
|
|
|
R |
|
|||||
|
|
|
|
|
287 |
|
|
||
83
12. ДРОССЕЛИРОВАНИЕ ГАЗОВ И ПАРОВ
12.1. Дросселирование газа
Дросселирование – необратимый процесс, в котором давление при прохождении газа через суживающееся отверстие уменьшается без совершения внешней работы. Если на пути струи газа или жидкости, протекающей по трубе или какому-либо другому каналу, встречается препятствие, приводящее к внезапному резкому сужению поперечного сечения струи, а затем сечение струи увеличивается, то давление протекающего газа (жидкости) за препятствием всегда оказывается меньшим, чем перед ним. Эффект падения давления струи рабочего тела и называется дросселированием (или мятием).
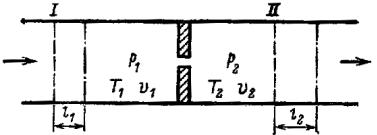
С процессом дросселирования приходится часто сталкиваться на практике, например, при движении воды через частично открытый водопроводный кран или при движении воздуха через не полностью открытый воздушный шибер. Физически падение давления за местным сопротивлением обусловлено диссипацией энергии потока. Оно зависит от природы рабочего тела, его состояния, сужения газопровода и скорости движения газа. Рассмотрим адиабатный процесс течения газа через трубу, имеющую местное сопротивление, например диафрагму, считая, что стенки трубы окружены идеальной теплоизоляцией, исключающей теплообмен с окружающей средой. Сечение трубы до и после диафрагмы считаем одинаковым, что дает возможность пренебречь изменением кинетической энергии потока. Рассмотрим массу газа (рис. 34), заключенную в данный момент между сечениями I (до местного сопротивления) и II (за сопротивлением).
Поскольку газ движется, то зафиксированные сечения газа (или невесомые поршни) I и II перемещаются вдоль трубы. Площадь сечения этих условных поршней обозначим S1
|
и S2 . |
|
Рис. 34. Дросселирование газа |
Давление, удельный объем и температуру газа до диафрагмы обозначим |
|
p1 , 1 |
и T1, после диаграммы – p2 , 2 и T2 . За некоторый промежуток времени |
поршень I переместится вдоль трубы на расстояние l1, поршень II – на расстояние l2. Так как давление и плотность газа за диафрагмой меньше, чем перед диафрагмой, то l1 l2. Для того чтобы переместить поршень I на расстояние l1,
нужно совершить работу, равную L1 p1l1 S1 или V1 p1 S1,
где V1 – объем газа, вытесненный поршнем I за рассматриваемый промежуток
времени через диафрагму, м3, |
V m; m – масса газа, |
прошедшего через |
||||
|
|
1 |
1 |
м3 |
|
|
дроссель, кг; |
– удельный объем газа до дросселирования, |
. |
||||
|
||||||
1 |
|
|
|
кг |
||
|
|
|
|
|||
84

Тогда L1 p1 1G.
Аналогично для второго поршня: L2 p2 2 G.
При перемещении газа за определенный промежуток времени совершается работа, равная алгебраической сумме работ: L p2 2 p1 1 G. Эта работа затрачивается на преодоление местного сопротивления, превращаясь в теплоту. Работа в адиабатном процессе может быть произведена только за счет уменьшения удельной внутренней энергии системы. Следовательно,
L u1 u2 G,
где u1 и u2 – удельная внутренняя энергия единицы массы газа соответственно
до и после диафрагмы, Дж.
кг
Приравнивая правые части уравнений L p2 2 p1 1 G и L u1 u2 G получаем:
p1 1 u1 p2 2 u2, |
i1 i2. |
Уравнение i1 i2 показывает, что в результате адиабатного дросселирования значения удельных энтальпий рабочего тела до и после местного сопротивления одинаковы.
Что же касается процесса, происходящего в самом дросселе, то следует заметить, что при течении внутри дросселя энтальпия газа (жидкости) может изменяться. Поток газа (жидкости) ускоряется, его кинетическая энергия возрастает и, следовательно, энтальпия уменьшается. После того как за дросселем сечение потока снова возрастает, поток замедляется (тормозится), его кинетическая энергия уменьшается и энтальпия увеличивается до прежнего значения.
Уравнение первого закона термодинамики для любого потока (и при отсутствии, и при наличии трения) имеет следующий вид:
dqвнеш di d gdh dlтехн.
Или в интегральной форме
q |
i i |
22 12 |
g h h l |
техн |
. |
|
|||||
внеш |
2 1 |
2 |
2 1 |
|
|
|
|
|
|
|
В случае адиабатного qвнеш горизонтального h2 = h1 потока, скорость кото-
рого в рассматриваемых точках относительно мала ( 2 1 0), при отсутствии технической работы lтехн 0 – именно такой поток рассматривается при анализе процесса дросселирования – уравнение принимает вид:
i2 i1,
что совпадает с выводом о неизменности удельной энтальпии в результате адиабатного дросселирования.
Рассмотрим горизонтальный поток, не совершающий технической работы при наличии трения: d dp dlтр . В случае, если скорость потока относи-
тельно мала, 0 (именно этот случай имеет место при дросселировании), по-
85

лучаем: dlтр dp. Т. е. в таком потоке давление вдоль потока dp 0 падает вследствие затраты потоком работы на преодоление трения (dlтр 0: работа,
производимая потоком, положительна). Если бы трение отсутствовало, то давление вдоль потока оставалось бы постоянным.
12.2. Изменение удельной энтропии и температуры при дросселировании
Дросселирование является необратимым процессом, так как часть энергии потока теряется на его завихрение перед диафрагмой и за ней и преобразуется в теплоту, которая при адиабатном течении передается рабочему телу. Если представить процесс, идущий в обратном направлении (например, в трубе, изображенной на рис. 34, изменить направление течения газа на обратное), то он по-прежнему будет сопровождаться падением давления при протекании газа через дроссель. Изменение удельной энтропии газа:
|
|
|
|
|
|
p2 |
s |
|
|
|
|
|
|
|
||
|
|
s |
2 |
s |
|
|
|
dp, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
i |
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
p1 |
|||||
|
|
|
|
|
p2 |
|
|
|
|
|
|
|||||
его можно записать в виде: s |
2 |
s |
|
dp, s |
2 |
s |
|
|
|
dp. |
||||||
|
|
|||||||||||||||
|
|
|
1 |
p T |
|
|
|
1 |
|
p |
|
T |
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
p2 p1. Из последнего |
||
Такая запись является наиболее удобной, так как |
|
|||||||||||||||
уравнения следует, что всегда s2 s1.
Для определения изменения температуры в процессе адиабатного дроссе-
T
лирования необходимо знать значение производной .
p i
|
|
|
|
|
|
|
|
|
|
T |
|
|
T |
|
|
T |
|
|
|
|||
|
|
Из соотношения |
|
|
|
|
|
|
|
1 |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
p i |
|
p T |
p |
|
|
|||||||
c |
|
|
i |
|
i |
|
|
|
|
|
|
|
|
T |
||||||||
p |
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
T p |
|
p T |
|
T p |
|
|
|
|
|
|
p i |
||||||||
с учетом соотношений
T T p
cp
.
|
|
T |
|
|
Величина |
|
|
|
называется коэффициентом адиабатного дросселирова- |
|
||||
|
|
|
||
|
|
p i |
|
|
ния или дифференциальным дроссель-эффектом, его обозначают i. В общем случае величина i отлична от нуля.
Явление изменения температуры газов и жидкостей при адиабатном дросселировании называется эффектом Джоуля – Томсона. Измеряя дифференциальный дроссель-эффект (весьма малую конечную разность температур T при такого же порядка разности давлений по обе стороны дросселя p), можно по
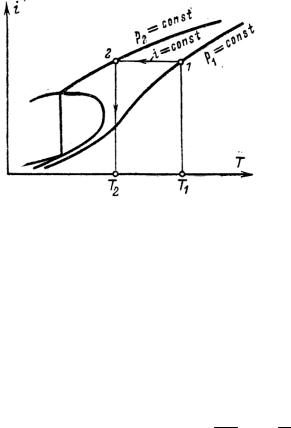
результатам этих измерений найти величину i , затем построить i, Т-
86
диаграмму исследуемого вещества, определить удельную теплоемкостьcp ,
удельный объем и т. д.
Изменение температуры газа (жидкости) при значительном перепаде давлений на дросселе называется интегральным дроссель-эффектом, он вычисляется из соотношения
p1
T2 T1 i dp,
p2
где T2, T1 – температуры дросселируемого вещества соответственно перед дросселем и за ним.
Интегральный дроссель-эффект может достигать весьма большой величины. Например, при дросселировании водяного пара от давления 29400 кПа и
температуры 450 С до давления, равного 98 кПа , температура пара уменьша-
ется до 180 С, т. е. на 270 С. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение |
величины |
интегрального |
|||||||||
|
адиабатного дроссель-эффекта удобно вы- |
||||||||||||
|
полнять с помощью i, Т-диаграммы дроссели- |
||||||||||||
|
руемого вещества (рис. 35). Если известно |
||||||||||||
|
состояние газа перед дросселем, т. е. его дав- |
||||||||||||
|
ление |
p1 |
|
и температура T1, и известно давле- |
|||||||||
|
ние за дросселем |
p2 , то, нанеся точку 1 и |
|||||||||||
|
найдя |
точку |
пересечения |
изоэнтальпы |
|||||||||
Рис. 35. i,Т-диаграмма |
i = const с изобарой |
|
p2 const , получим тем- |
||||||||||
пературу за дросселем T2. |
|
||||||||||||
Знак дроссель-эффекта |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
T |
|
|
|
|
|
||
|
|
|
|
|
|
T |
|
|
|||||
Проанализируем соотношение |
|
T |
|
|
|
|
|
p |
|
. Поскольку всегда |
|||
|
|
|
p |
|
|
|
cp |
|
|
|
|
||
cp 0, то знак коэффициента |
|
|
i |
|
|
|
|
|
|||||
i определяется знаком стоящей в числителе |
|||||||||||||
правой части уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что если T p
руемого вещества возрастает.
T , то i 0, и тогда температура дроссели-
|
|
|
|
i |
0, и тогда температура дросселируемого вещест- |
||
Если |
|
|
|
, то |
|||
|
|
||||||
|
T p |
|
T |
|
|
||
ва уменьшается.
87
|
|
|
|
|
i |
0, и тогда температура дросселируемого веще- |
||
Если |
|
|
|
|
, то |
|||
|
|
|||||||
|
|
T p |
|
T |
|
|
||
|
|
|
|
|
||
ства не меняется. Для идеального газа характерно |
|
|
|
|
, тогда идеальный |
|
|
|
|||||
|
|
T p |
|
T |
||
газ дросселируется без изменения температуры.
Таким образом, для газа, подчиняющегося уравнению Ван-дер-Ваальса, эффект Джоуля – Томсона не равен нулю.
Как показывает опыт, для одного и того же вещества i оказывается различным в зависимости от области состояния. Состояние газа (жидкости), в котором i равен нулю, называется точкой инверсии эффекта Джоуля – Томсона. Геометрическое место точек инверсии на диаграмме состояния данного вещества называется кривой инверсии. Точки на кривой инверсии удовлетворяют уравнению i 0. Пользуясь этим условием, можно найти кривую инверсии с помощью уравнения состояния вещества.
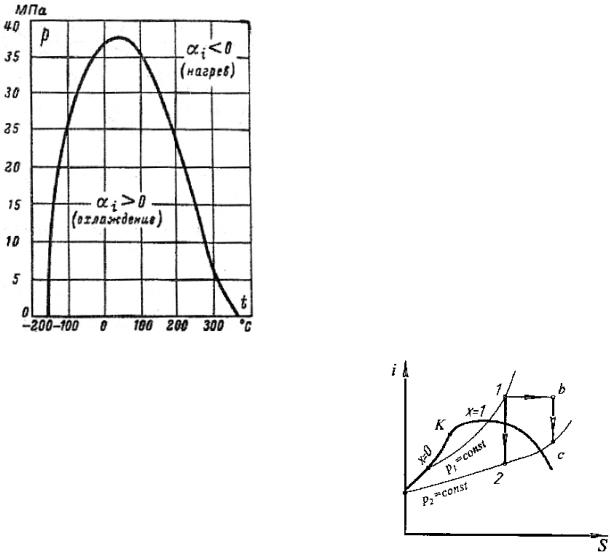
В качестве примера на рис. 36 приведена кривая инверсии азота в p,t-диаграмме. Внутри области, ограниченной кривой инверсии i 0, т. е. газ при дросселировании
охлаждается. Вне этой области i 0, т. е.
температура газа при дросселировании повышается. Аналогичный характер имеют кривые инверсии других веществ.
Процесс дросселирования используют для регулирования работы паросиловых установок, так как с увеличением дросселирования уменьшаются расход рабочего тела и располагаемая работа (теплоперепад). Действительно, если без дросселирования располагаемая работа равна i1 i2 (рис. 37), то
Рис. 36. Кривая инверсии азота
при наличии процесса 1–b располагаемая ра-
бота |
уменьшается и |
становится равной |
|
ib ic |
i1 i2. Так как при дросселирова- |
||
нии пара перед турбиной с давлением 10 |
кПа |
||
и температурой 500 С |
до давления 5 |
кПа |
|
расход пара уменьшается в два раза, а адиабатный теплоперепад на 16 %, то мощность турбины снижается примерно на 53 %.
Рис. 37. Дросселирование водяного пара перед паровой турбиной
88
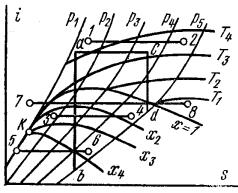
12.3. Дросселирование водяного пара
Исследование процесса дросселирования водного пара наглядно производится по i, S-диаграмме (рис. 38), в которой процесс мятия можно условно изобразить горизонтальной линией, так как горизонталь есть только вспомогательное построение для нахождения параметров состояния конечной точки и не имеет физического смысла в промежуточных точках.
Пусть водяной пар дросселируется от состояния a до состояния c. От точки a до давления p5 разность энтальпий выражается отрезком ab; от точки c разность энтальпий выражается отрезком cd , который значительно меньше отрезка ab, т. е. работоспособность пара резко падает. Чем больше мятие пара, тем меньше его работоспособность. Из диаграммы видно, что если подвергается мятию перегретый пар (процесс 1–2), то
давление и температура уменьшаются, а объем, удельная энтропия и степень перегрева увеличиваются. При мятии пара высокого давления и небольшого перегрева (процесс 7–8) пар сначала переходит в сухой насыщенный, затем во влажный, потом опять в сухой насыщенный и снова перегретый. При дросселировании кипящей жидкости (процесс 5–6) она частично испаряется с увеличением степени сухости. При дросселировании влажного пара степень сухости его увеличивается (процесс 3–4).
Процесс дросселирования является необратимым процессом, который сопровождается увеличением удельной энтропии. С ростом удельной энтропии всегда понижается работоспособность газа или пара.
Контрольные вопросы
1.Какой процесс называется дросселированием и где он встречается?
2.Какие величины изменяются и какие остаются постоянными за суженным отверстием?
3.Уравнение процесса дросселирования.
4.Почему процесс дросселирования нельзя назвать изоэнтальпийным?
5.Как изменяется температура идеального газа при дросселировании?
6.Эффект Джоуля – Томсона и его уравнение.
7.Что такое дифференциальный и интегральный эффекты дросселирования?
8.Дросселирование реальных газов.
9.Что называется точкой и температурой инверсии?
10.Дифференциальный эффект Джоуля – Томсона для газов, подчиняющихся уравнению Ван-дер-Ваальса.
11.Когда и при каких условиях температура реального газа при дросселировании повышается, понижается и остается без изменения?
12.Исследование процесса дросселирования водяного пара по i,S-диаграмме.
13.Изменение работоспособности водяного пара при дросселировании.
89
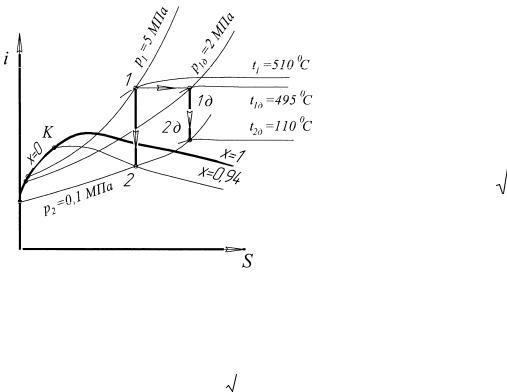
Задача
Определить скорость и степень сухости водяного пара в выходном сечении, а также отношение расходов пара для двух сопл Лаваля:
1)пар на входе в сопло имеет параметры p1 5 МПа и t1 510 0С, а в выходном сечении сопла давление пара p2 0,1 МПа;
2)перед поступлением в сопло пар дросселируется от заданного выше дав-
ления p1 до давления p1д 2 МПа, а затем в сопле расширяется до давления p2 0,1 МПа.
Решение
1) Определим располагаемое отношение давлений расп :
|
расп |
|
р2 |
|
0,1 |
0,02 |
|
кр |
0,55. |
р |
|
||||||||
|
|
5 |
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
Давление в критическом сечении сопла Лаваля: pкр кр р1 0,55 5 2,75 МПа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По i, S-диаграмме (рис. 39) пара- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
метры водяного пара в состоянии 1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при p1 = 5 МПа и t1 = 510 C: |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 3475 |
кДж |
|
, |
|
0,07 |
м3 |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
кг |
|
|
|
|
|
|
|
|
|
|
|
кг |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кДж |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
7,1 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кгК |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Критическая скорость: |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кр 44,72 |
|
|
|
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i1 iкр1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения |
|
i |
|
|
|
|
3265 |
кДж |
|
– |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кр1 |
кг |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
удельной |
энтальпии |
|
в критической |
||||||||||||||||||
|
|
|
Рис. 39. К задаче 1 |
|
|
|
|
|
точке и кр1 0,11 |
|
|
м3 |
|
– критического |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
кг |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кДж |
|
|
|
|
|||||
объема |
определяем |
|
|
на |
пересечении |
|
|
S2 7,1 |
|
|
|
и |
|||||||||||||||||||||||
|
|
кгК |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
pкр 2,75 МПа, кр 44,72 |
|
|
|
|
|
648,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
3475 3265 |
(рис. 39). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
i, S-диаграмме параметры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
По |
водяного |
пара |
|
в |
|
|
состоянии |
|
при |
||||||||||||||||||||||||
p |
|
0,1 |
МПа и |
S |
S |
|
7,1 |
кДж |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
кгК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
i2 |
2550 |
|
кДж |
, 2 1,6 |
м3 |
|
, t2 100 0С, |
|
x2 0,94. |
|
|
|
||||||||||||||||||||
|
|
|
|
кг |
|
кг |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
90
