Serov_ch_1 / !poz049

51

C = ∆Q/∆ϕ ,

где ∆Q — заряд, сообщенный проводнику (конденсатору); ∆φ — изменение потенциала, вызванное этим зарядом.

где S—площадь пластин (каждой пластины); d—расстояние между ними; ε — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электрическая емкость плоского конденсатора, заполненного п слоями диэлектриков толщиной di; каждый с диэлектрическими проницаемостями εi; (слоистый конденсатор),

C = ε0 S .

d1 ε1 + d2 ε2 +... + dn εn

Электрическая емкость C последовательно соединенных конденсаторов:

Энергия заряженного проводника выражается через заряд Q, потенциал φ и электрическую емкость C проводника следующими соотношениями:

где C — электрическая емкость конденсатора; U — разность потенциалов на его пластинах.

Объемная плотность энергии (энергия электрического поля, приходящаяся на единицу объема)

ω = 12 ε0εE 2 = 12 ED,

где E — напряженность электрического поля в среде с диэлектрической проницаемостью ε; D — электрическое смещение.

где Q — количество электричества, прошедшее через поперечное сечение проводника за время t.

Плотность электрического тока есть векторная величина, равная отношению силы тока к площади перечного сечения проводника:

rj = I kr ,

положительных носителей заряда.

52

где ρ — удельное сопротивление вещества проводника; l — его длина. Зависимость удельного сопротивления от температуры

ρ=ρ0(1+αt),

где ρ и ρ0 — удельные сопротивления соответственно при t и 0°С; t — температура (по шкале Цельсия); α — температурный коэффициент сопротивления.

Сопротивление соединения проводников:

источников тока, входящих в участок; U — напряжение на участке цепи; R— сопротивление цепи (участка цепи).

Правила Кирхгофа. Первое правило: алгебраическая сумма сил токов, сходящихся в узле, равна нулю, т. е.

n

∑Ii = 0, где п — число токов, сходящихся в узле.

i=1

Второе правило: в замкнутом контуре алгебраическая сумма напряжений на всех участках контура равна алгебраической сумме электродвижущих сил, т. е.

Закон Джоуля — Ленца Q = I 2 Rt ,

где Q — количество теплоты, выделяющееся в участке цепи за время t. Закон Джоуля

— Ленца справедлив при условии, что участок цепи неподвижен и в нем не совершаются химические превращения.

Плотность тока j, средняя скорость <u> упорядоченного движения носителей заряда и их концентрация п связаны соотношением

j = ne u ,

где е — элементарный заряд.

53

Закон Ома в дифференциальной форме j =σE ,

где σ — удельная проводимость проводника; E — напряженность электрического поля.

Закон Джоуля — Ленца в дифференциальной форме ω =σE 2 , где ω — объемная плотность тепловой мощности.

Примеры решения задач

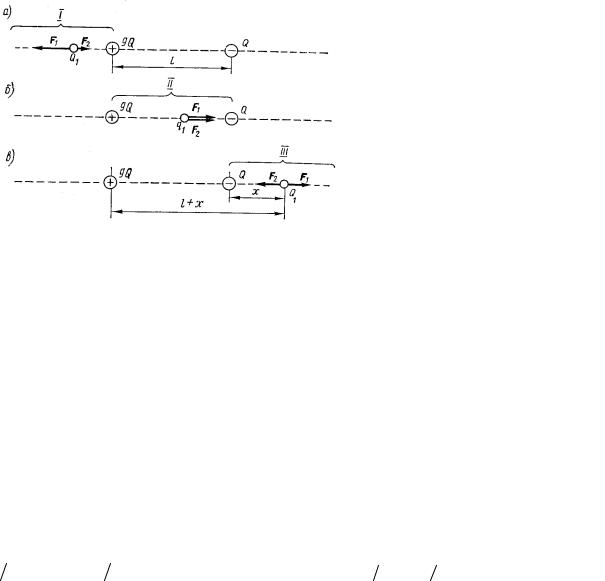
Пример 1. Два точечных заряда 9Q и -Q закреплены на расстоянии l = 50 см друг от друга. Третий заряд Q1 может перемещаться только вдоль, прямой, проходящей через заряды. Определить положение заряда

Q1, при котором он будет находиться в равновесии. При каком знаке заряда Q1 равновесие будет устойчивым?

Решение. Заряд Q1 находится в равновесии в том случае, если геометрическая сумма сил, действующих на него, равна нулю. Это значит, что на заряд Q1 должны действовать две силы, равные по модулю и противоположные по направлению. Рассмотрим, на каком

из трех участков I , II , III может быть выполнено это условие. Для определенности будем считать, что заряд Q1 - положительный.

На участке 1 на заряд Q1 будут действовать две противоположно направленные силы: F1 и F2 . Сила F1 , действующая со стороны заряда 9Q, в любой точке этого участка больше силы F2 , действующей со стороны заряда -Q , так как больший заряд

9Q находится всегда ближе к заряду Q1 ,чем меньший (по модулю) заряд -Q. Поэтому равновесие на этом участке невозможно.

F2 хотя и равны по модулю, но сонаправлены).

Определим знак заряда Q1, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Рассмотрим смещение

54

заряда Q1 в двух случаях: когда заряд положителен и отрицателен.

Если заряд Q1 положителен, то при смещении его влево обе силы F1 и F2 возрастают. Так как сила F1 возрастает медленнее, то результирующая сила,

действующая на заряд Q1 , будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд Q1 будет удаляться от положения равновесия. То же происходит и при смещении заряда Q1 вправо. Сила F2 убывает

быстрее, чем F1 . Геометрическая сумма сил в этом случае направлена вправо. Заряд

под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.

Если заряд Q1 отрицателен, то его смещение влево вызовет увеличение сил F1 и F2 , но сила F1 возрастает медленнее, чем F2 , т. е. Fr2 > Fr1 . Результирующая сила будет направлена вправо. Под ее действием заряд Q1 возвращается к положению равновесия. При смещении Q1 вправо сила F2 убывает быстрее, чем F1 т. е. Fr2 > Fr1 ,

результирующая сила направлена влево и заряд Q1 опять будет возвращаться к положению равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда Q1 несущественна.

Пример 2. Три точечных заряда Q1 = Q2 = Q3 = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q4 нужно поместить в центре

треугольника, чтобы указанная система зарядов находилась в равновесии? Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например Q1 ,

находился в равновесии. Заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю:

F2 + F3 + F4 = F + F4 = 0 , (1)

где F2 , F3 , F4 - силы, с которыми соответственно

действуют на заряд Q1 , заряды Q2 , Q3 , Q4 F - равнодействующая сил F2 и F3 .

Из геометрических построений в равностороннем треугольнике следует, что

55

С учетом этого формула (2) примет вид Q4 = Q1 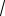3 . Произведем вычисления: Q4 = 10−9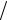 3 Кл = 5,77 10−10 Кл = 577 пКл.

Следует отметить, что равновесие системы зарядов будет неустойчивым.

Пример 3. Тонкий стержень длиной l=30 см несет равномерно распределенный по длине заряд с линейной плотностью τ=1 мкКл/м. На

расстоянии r0=20 см от стержня находится заряд Q1=10 нКл, равноудаленный от концов стержня. Определить силу F взаимодействия точечного заряда с заряженным стержнем.

Решение. Закон Кулона позволяет вычислить силу взаимодействия точечных зарядов. По условию задачи, один из зарядов не является точечным, а представляет собой заряд, равномерно распределенный по длине стержня. Однако если выделить на стержне

дифференциально малый участок длиной dl , то находящийся на нем заряд

можно рассматривать как точечный и тогда по закону Кулона сила взаимодействия между зарядами Q1 и dQ:

разложим его на две составляющие: dF1 , перпендикулярную стержню, и dF2 , параллельную ему.

F1 = Q1τ sin β. 2πε0 r0

В силу симметрии расположения заряда Q1 относительно стержня интегрирование второго выражения дает нуль:

56

Решение. Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других

зарядов. Поэтому напряженность E электрического поля в искомой точке может быть найдена как геометрическая сумма

57

В соответствии с принципом суперпозиции электрических полей потенциал ϕ результирующего поля, создаваемого двумя зарядами Q1 и Q2 , равен алгебраической сумме потенциалов;

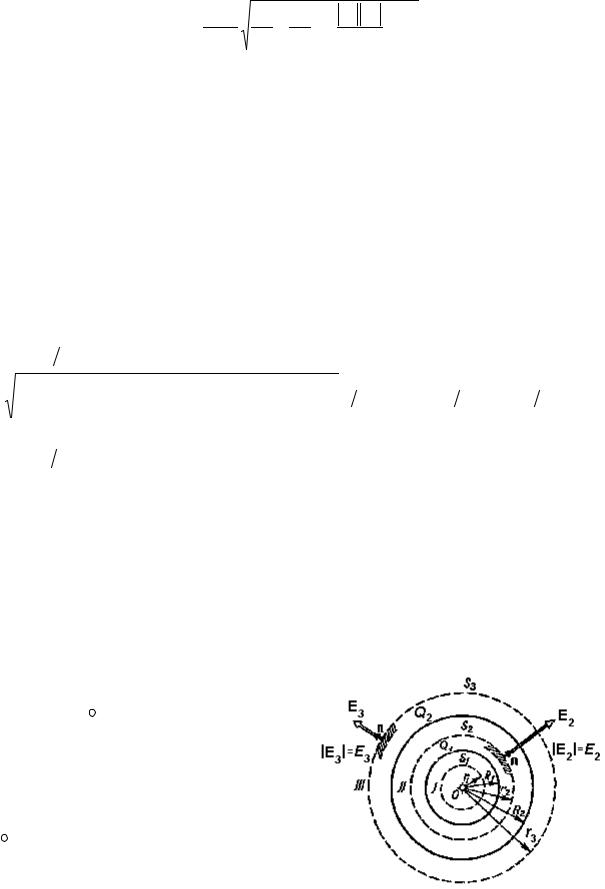
Пример 5. Две концентрические проводящие сферы радиусами R1 =6см и R2 =10см несут соответственно заряды Q1 =1нКл и Q2 = −0,5 нКл. Найти напряженность Е поля в точках, отстоящих от центра сфер на расстояниях r1 =5 см, r2 =9 см, r3 = 15 см.

Построить график.

Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях: области I ( r1 < R1 ), области II

(R1 < r2 < R2 ), области III (r3 > R2 )

1.Для определения напряженности E1 в области I проведем гауссову поверхность

S1 радиусом r1 и воспользуемся теоремой Остроградского-Гаусса:

∫En dS = 0

S1

(так как суммарный заряд, находящийся внутри гауссовой поверхности, равен

удовлетворяющих условию r1 < R1 , будет

58

Q

E2 = 4πε0r22 (1)

3.В области III гауссова поверхность проводится радиусом r3 . Обозначим1

напряженность Е области III через E3 и учтем, что в этом случае гауссова

поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен Q1 + Q2 . Тогда

59

справа) E3 (R2 ) = (Q1 − Q2 )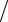(4πε0 R22 ) = 0,45 кВ/м. Таким образом, функция E(r) в точках r = R1 , и r = R2 терпит разрыв.

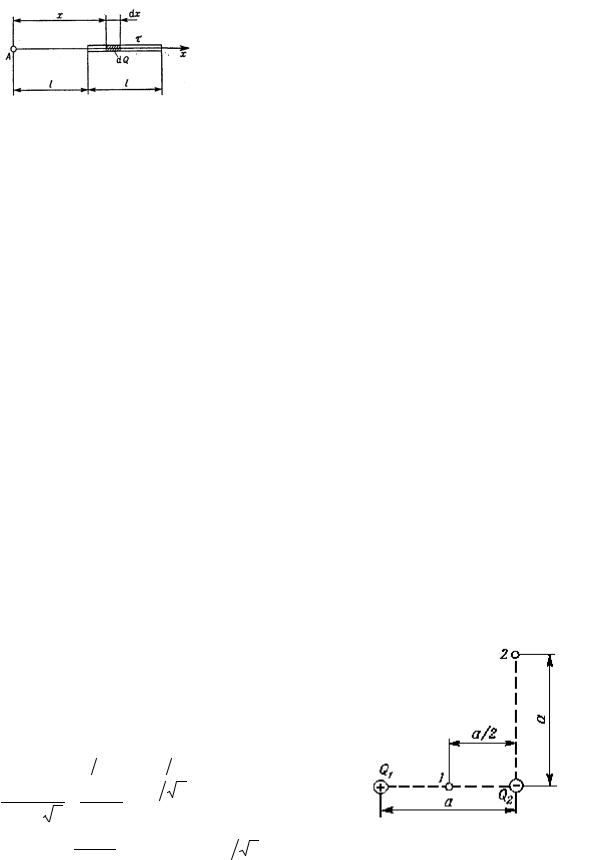
График зависимости E(r) представлен на рисунке.

Пример 6. На тонком стержне длиной l равномерно распределен заряд с линейной

расположенной на оси стержня и удаленной от его ближайшего конца на расстояние l .

Решение. В задаче рассматривается поле, создаваемое распределенным зарядом. В этом случае

поступают следующим образом. На стержне выделяют малый участок длиной dx . Тогда на этом участке будет сосредоточен заряд dQ = τdx , который можно считать

точечным. Потенциал dϕ, создаваемый этим точечным зарядом в точке А , можно определить по формуле

Согласно принципу суперпозиции электрических полей, потенциал электрического поля, создаваемого заряженным стержнем в точке A , найдем интегрированием этого

Подставим числовые значения физических величин в СИ ( τ = 10 10−9 Кл/м 1(4πε0 ) = 9 109 м/Ф) и произведем вычисления:

ϕ = 9 109 10 10−9 0,693B = 62,4B .

Пример 7. Электрическое поле создается двумя зарядами Q1 = 4 мкКл и Q2 = −2 мкКл, находящимися на расстоянии а= 0,1 м друг от друга. Определить работу A1,2 сил поля по перемещению заряда Q = 50 нКл из точки 1 в точку 2 .

Решение. Для определения работы A1,2 сил поля

воспользуемся соотношением

A1,2 = Q(ϕ1 − ϕ2 )

Применяя принцип суперпозиции электрических

60

напряженностью Е, созданном зарядом другой пластины конденсатора. Следовательно, на первый заряд действует сила

Пример 9. Конденсатор емкостью C1 = 3мкФ был заряжен до разности потенциалов U1 =40В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью C2 =5мкФ. Какая энергия

израсходуется на образование искры в момент присоединения второго конденсатора? Решение. Энергия, израсходованная на образование искры,

общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим

где U2 - разность потенциалов на зажимах батареи конденсаторов.