
Serov_Fizika_ch_2 / !poz017
.pdf
51
Примеры решения задач
Пример 1. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.
Р е ш е н и е. Для определения энергии фотона воспользуемся сериальной формулой для водородоподобных ионов:
1 λ = RZ 2 (1 n12 −1 n22 ), |
(1) |
где λ - длина волны фотона; R - постоянная Ридберга; Z - заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n1 - номер орбиты, на которую перешел электрон; n2 - номер орбиты, с которой перешел электрон (n1 и n2 - главные квантовые числа).
Энергия фотона ε выражается формулой
ε = hc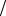 λ.
λ.
Поэтому, умножив обе части равенства (1) на hс, получим выражение для энергии фотона:
ε = RhcZ 2 (1 n12 −1
n12 −1 n22 ).
n22 ).
Так как Rhc есть энергия ионизации Ei атома водорода, то
ε = Ei Z 2 (1 n12 −1
n12 −1 n22 ).
n22 ).
Вычисления выполним во внесистемных единицах: Ei = 13,6 эВ (см. табл. 1
Приложения); Z=1; n1=2; n2=4:
2 |
1 |
− |
1 |
|
3 16 эВ = 2,25 эВ. |
|
ε =13,6 1 |
|
22 |
42 |
эВ =13,6 |
||
|
|
|
|
|
||
Пример 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля электрона для двух случаев: 1) U1 = 51 В; 2) U2 = 510 кв.
Р е ш е н и е. Длина волны де Бройля для частицы зависит от ее импульса p и определяется формулой
λ = h p , |
(1) |
где h - постоянная Планка.
Импульс частицы можно определить, если известна ее кинетическая энергия T. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).
В нерелятивистском случае
p = |
2m0T , |
(2) |
|
где m0 - масса покоя частицы. |
|
|
|
В релятивистском случае |
(2E0 +T )T / c, |
(3) |
|
p = |
|||
где E0 = m0c2 - энергия покоя частицы. |
|
||
Формула (1) с учетом соотношений (2) и (3) запишется: |
|
||
в нерелятивистском случае |
|
|
|
λ = |
h |
, |
(4) |
|
2m T |
|
|
|
0 |
|
|

52
в релятивистском случае
λ = |
h |
(5) |
(2E0 + T )T / c . |
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U1=51 В и U2=510кВ, с энергией покоя электрона и в зависимости от этого решим, какую из формул (4) или (5) следует применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона прошедшего ускоряющую разность потенциалов U,
T = eU.
В первом случае T1 = eU = 51эВ = 0,51 10-4МэВ, что много меньше энергия покоя электрона Е0 = m0c2 = 0,51МэВ. Следовательно, в этом случае можно применить формулу (4). Для упрощения расчетов заметим, что Т1 = 10-4m0c2. Подставив это выражение в формулу (4), перепишем ее в виде
λ = |
h |
|
= |
102 |
h |
. |
|
2m 10−4 |
m c2 |
2 |
m0c |
||||
|
|
|
|||||
|
0 |
0 |
|
|
|
|
Учитывая, что h/m0c есть комптоновская длина волны Λ, получаем
λ1 =102 Λ
 2 .
2 .
Так как Λ = 2,43 пм (см. табл. 1 Приложения), то
λ1 =102 2,43
 2 пм =171пм.
2 пм =171пм.
Во втором случае кинетическая энергия
T2 = eU2 = 510 кэВ = 0,51 МэВ, т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Учитывая, что T2 = 0,51 МэВ= m0c2, по формуле (5) находим
λ2 = |
h |
= |
h |
, |
(2m0c2 + m0c2 )m0c2 / c |
3m0c |
или
λ2 = Λ
 3 .
3 .
Подставим значение Λ и произведем вычисления:
λ2 = 2,43
 3пм =1,40 пм.
3пм =1,40 пм.
Пример 3. Кинетическая энергия электрона в атоме водорода составляет величину порядка T = 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.
Р е ш е н и е. Соотношение неопределенностей для координаты и импульса имеет вид
∆x∆px ≥ h, |
(1) |
где ∆x - неопределенность координаты частицы (в данном случае электрона); ∆px - неопределенность импульса частицы (электрона); h - постоянная Планка.
Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью
∆x = l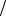 2.
2.

53
Соотношение неопределенностей (1) можно записать в этом случае в виде
(l 2)∆px ≥ h,
2)∆px ≥ h,
откуда
(2)
Физически разумная неопределенность импульса ∆px во всяком случае не должна превышать значения самого импульса px, т.е. ∆px≤px. Импульс px связан кинетической
энергией Т соотношением px = |
2mT . Заменим ∆px значением 2mT (такая замена |
|
не увеличит l). Переходя от неравенства к равенству, получим |
||
lmin = 2h |
2mT . |
(3) |
Проверим, дает ли полученная формула единицу длины. Для этого в правую часть формулы (3) вместо символов величин подставим обозначения их единиц:
|
[h] |
|
|
|
|
1 2 |
|
|
|
|
|
2 |
|
2 |
1 2 |
|
||
|
1Дж с |
|
|
|
1Дж |
|
1кг |
м |
с |
|
|
|||||||
|
|
= |
|
|
|
|
|
1c = 1м. |
||||||||||
|
|
= |
|
|
|
|
|
1с = |
|
|
|
|
|
|
|
|
||
1 2 |
1 2 |
|
|
1кг |
|
|
||||||||||||
|
([m][T ]) |
(1кг 1Дж) |
|
|
|
1кг |
|
|
|
|
|
|
||||||
Найденная единица является единицей длины. |
|
|
|
|
|
|||||||||||||
Произведем вычисления: |
|
2 1,05 10−34 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
lmin = |
|
|
|
|
|
|
м =1,24 10−10 м = 0,124 нм. |
||||||||
|
|
|
2 9,1 10−13 1,6 10−19 10 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 4. Вычислить дефект массы и энергию связи ядра 37 Li.
Р е ш е н и е. Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра ∆m и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т.е.
(1)
где Z - атомный номер (число протонов в ядре); A - массовое число (число нуклонов, составляющих ядро); mр, mn, mя - соответственно массы протона, нейтрона и ядра.
В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в нее входила масса mа нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома: ma = mя + Zme, откуда
mШ = ma −Zme . |
(2) |
Выразив в равенстве (1) массу ядра по формуле (2), получаем |
|
∆m =Zmp + (A - Z)mn - ma +Zme, или |
|
∆m = Z (mp + me )+ (A − Z )mn − me. |
|
Замечая, что mp + me = mH, где mH - масса атома водорода, окончательно находим |
|
∆m = ZmH + (A − Z )mn − ma . |
(3) |
Подставив в выражение (3) числовые значения масс (см. табл. 13 и 15 Приложения), получим
∆m = [3 1,00783 + (7 −3) 1,00867 −7 0,1601 ]а.е.м. = 0,04216 а.е.м.
В соответствии с законом пропорциональности массы и энергии
E = c2 ∆m, (4)
где с - скорость света в вакууме.
Коэффициент пропорциональности с2 может быть выражен двояко:
54
с2 = 9·1016 м2/с2, или с2 = ∆E/∆m = 9·1016 Дж/кг. |
единицами, то с2 = |
Если вычислить энергию связи, пользуясь внесистемными |
|
931МэВ/а.е.м. С учетом этого формула (4) примет вид |
|
E = 931∆m (МэВ). |
(5) |
Подставив найденное значение дефекта массы ядра в формулу (5), получим |
|
E = 931 0,04216 МэВ = 39,2 МэВ. |
|
Примечание. Термин «дефект массы» часто применяют в другом смысле: дефектом массы ∆ называют разность между массой нейтрального атома данного изотопа и его массовым числом A:
∆ = ma - A. Эта величина особого физического смысла не имеет, но ее использование позволяет в ряде случаев значительно упростить вычисления. В настоящем пособии всюду имеется в виду дефект массы ∆m, определяемый формулой (1).
Пример 5. При соударении α - частицы с ядром бора 105 B произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода 11H . Определить порядковый номер и массовое число второго
ядра, дать символическую запись ядерной реакций и определить ее энергетический эффект.
Р е ш е н и е. Обозначим неизвестное ядро символом ZA X . Так как α-частица представляет собой ядро гелия 24 He , запись реакции имеет вид
24 He+105B→11H +ZAX .
Применив закон сохранения числа нуклонов, получим уравнение
4 + 10 = 1 + A, откуда A = 13. Применив закон сохранения заряда, получим уравнение 2 + 5 = 1 + Z, откуда Z = 6. Следовательно, неизвестное ядро является ядром атома изотопа углерода 136 C.
Теперь можем записать реакцию в окончательном виде:
24 He+105 B→11H +136 C.
Энергетический эффект Q ядерной реакции определяется по формуле
Q = 931[(mHe + mB )− (mH + mC )].
Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках - массы ядер - продуктов реакции. При числовых подсчетах по этой формуле массы ядер заменяют массами нейтральных атомов. Возможность такой замены вытекает из следующих соображений.
Число электронов в электронной оболочке нейтрального атома равно его зарядовому числу Z. Сумма зарядовых чисел исходных ядер равна сумме зарядовых чисел ядер - продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода.
Очевидно, что при вычитании суммы масс нейтральных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут и мы получим тот же результат, как если бы брали массы ядер. Подставив массы атомов (см. Табл. 13 Приложения) в расчетную формулу, получим
Q = 931(4,00260 +10,01294)− (1,00783 +13,00335)МэВ = 4,06 М эВ.

55
Пример 6. Определить начальную активность A0 радиоактивного препарата магния 27 Mg массой m = 0,2 мкг, а также его активность A через время t = 6ч. Период полураспада T1/2 магния считать известным.
Р е ш е н и е. Активность A изотопа характеризует скорость радиоактивного распада
иопределяется отношением числа dN ядер, распавшихся за интервал времени dt, к этому интервалу:
A = −dN dt . |
(1) |
Знак «-» показывает, что число N радиоактивных ядер с течением времени убывает. Для того чтобы найти dN/dt, воспользуемся законом радиоактивного распада:
N = N0e−λt , |
(2) |
где N - число радиоактивных ядер, содержащихся в изотопе, в момент времени t; N0 - число радиоактивных ядер в момент времени, принятый за начальный (t = 0); λ - постоянная радиоактивного распада.
Продифференцируем выражение (2) по времени:
dN dt = −λN0e−λt . |
(3) |
Исключив из формул (1) и (3) dN/dt, находим активность препарата в момент времени t:
A = λN0e−λt . |
(4) |
Начальную активность A0 препарата получим при t=0: |
(5) |
A0 = λN0 . |
Постоянная радиоактивного распада λ связана с периодом полураспада T1/2 соотношением
(6)
Число N0 радиоактивных ядер, содержащихся в изотопе, равно произведению постоянной Авогадро NA на количество вещества ν данного изотопа:
N0 =νN A = |
m |
N A , |
(7) |
|
M |
||||
|
|
|
||
где m - масса изотопа; M - молярная масса. |
|
|||
С учетом выражений (6) и (7) формулы (5) и (4) принимают вид
A = |
m |
|
ln 2 |
N |
|
. |
(8) |
|||||
|
|
|
|
|
A |
|||||||
0 |
|
M T1 2 |
|
|
||||||||
|
|
|
|
|
||||||||
|
m |
|
ln 2 |
|
|
|
ln 2 t |
|
||||
A = |
|
N AeT1 2 . |
(9) |
|||||||||
|
|
|||||||||||
|
M T1 2 |
|
|
|
||||||||
Произведем вычисления, учитывая, что T1/2 = 10 мин = 600 с (см. табл. 14
Приложения), 1n2 = 0,693, t = 6ч = 6 3,6 103с = 2,16. 104с:
|
|
0,2 10−9 |
0,693 |
|
|
|
23 |
|
|
|
12 |
|
||||||
A = |
|
|
|
|
|
|
|
6,02 10 |
|
|
Бк = 5,13 10 |
Бк = 5,13 ТБк; |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
27 10−3 |
600 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0,693 |
|
|
|
||||||
|
0,2 10−9 |
|
0,693 |
|
|
|
23 |
|
− |
2,16 10 |
4 |
|
||||||
A = |
6,02 |
10 |
e |
600 |
Бк = 81,3 Бк. |
|||||||||||||
27 10−3 |
600 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 7. Вычислить максимальную энергию εF (энергию Ферми), которую могут иметь свободные электроны в металле (медь) при температуре T=0 К. Принять, что на каждый атом меди приходится по одному валентному электрону.

56
Р е ш е н и е. Максимальная энергия εF, которую могут иметь электроны в металле
при T=0К, связана с концентрацией свободных электронов соотношением |
|
εF = h2 (3π 2n)2 3 (2m), |
(1) |
где h - постоянная Планка; m - масса электрона.
Концентрация свободных электронов по условию задачи равна концентрации атомов, которая может быть найдена по формуле
n = ρN A M , |
|
|
|
|
|
|
(2) |
где ρ - плотность меди; NA - постоянная Авогадро; M - молярная масса. |
|||||||
Подставляя выражение n в формулу (1), получаем |
2 3 |
||||||
|
|
h2 |
|
N |
A |
|
|
εF |
= |
|
3π 2 ρ |
|
|
. |
|
|
M |
||||||
|
|
2m |
|
||||
Произведем вычисления: |
|
|
|
|
|
|
||||||
ε |
|
= |
(1,05 10−34 )2 |
3 (3,14)2 |
8,9 103 |
|
6,02 10−23 |
2 3 |
Дж =1,18 10−18 |
Дж = 7,4 эВ. |
||
F |
|
−31 |
|
−3 |
|
|||||||
|
|
2 9,1 10 |
|
|
|
64 10 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
Пример 8. Кремниевый образец нагревают от температуры t1=0°С до температуры t2=10°С. Во сколько раз возрастает его удельная проводимость?
Р е ш е н и е. Удельная проводимость γ собственных полупроводников связана с
температурой T соотношением
γ =γ0e−∆E (2kT ),
(2kT ),
где γ0 - константа; ∆E - ширина запрещенной зоны. Следовательно,
γ1 |
|
e |
−∆E (2kT ) |
|
∆E |
|
1 |
|
1 |
|
|
= |
|
= exp |
|
− |
.' |
||||||
γ |
|
e−∆E (2kT ) |
2k |
|
|
||||||
2 |
|
|
T T |
|
|||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
Полагая для кремния ∆E = 1,1 эВ, произведем вычисления:
γ |
1 |
= exp |
1,76 |
10 |
−19 |
1 |
− |
1 |
|
= 2,28. |
|
|
|
|
|
|
|
|
|
||||
γ2 |
|
|
|
|
|
||||||
|
2(1,38 10−23 ) |
273 |
|
283 |
|
|
|||||
Контрольная работа №6 Таблица вариантов
Вариант |
|
|
|
Номера задач |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
610 |
620 |
630 |
640 |
650 |
660 |
670 |
680 |
1 |
601 |
611 |
621 |
631 |
641 |
651 |
661 |
671 |
2 |
602 |
612 |
622 |
632 |
642 |
652 |
662 |
672 |
3 |
603 |
613 |
623 |
633 |
643 |
653 |
663 |
673 |
4 |
604 |
614 |
624 |
634 |
644 |
654 |
664 |
674 |
5 |
605 |
615 |
625 |
635 |
645 |
655 |
665 |
675 |
6 |
606 |
616 |
626 |
636 |
646 |
656 |
666 |
676 |
7 |
607 |
617 |
627 |
637 |
647 |
657 |
667 |
677 |
8 |
608 |
618 |
628 |
638 |
648 |
658 |
668 |
678 |
9 |
609 |
619 |
629 |
639 |
649 |
659 |
669 |
679 |
57
601. Определите магнитный момент электрона, находящегося в атоме водорода на первой боровской орбите. Сравните полученный результат с магнетоном Бора.
602.Определите магнитный момент электрона, находящегося в атоме водорода на пятой боровской орбите. Сравните полученный результат с магнетоном Бора.
603.Найдите напряженность электрического поля ядра на первой и четвертой боровских орбитах атома водорода.
604.Найдите для основного состояния атома водорода:
а) отношение кулоновской и гравитационной сил взаимодействия между электроном и ядром; б) индукцию магнитного поля в центре атома, обусловленную орбитальным
движением электрона.
605.Найдите для атома водорода, находящегося в состоянии, характеризуемом главным квантовым числом, равным 2:
а) отношение кулоновской и гравитационной сил взаимодействия между электроном и ядром; б) индукцию магнитного поля в центре атома, обусловленную орбитальным движением электрона.
606.Найдите для электрона, находящегося в атоме водорода на n - й боровской орбите, отношение орбитального магнитного момента к орбитальному механическому моменту.
607.Найдите в длинах волн спектральные интервалы, в которых заключены серии Лаймана, Бальмера и Пашена для атомарного водорода. Изобразите в шкале длин волн их относительное расположение, выделив видимую часть спектра.
608.Какие линии содержит спектр поглощения атомарного водорода в диапазоне длин волн от 94,5 до 130,0 нм?
609.На какой орбите скорость электрона в атоме водорода равна 734 км/с?
610.Наибольшая длина волны спектральной водородной линии серии Лаймана 121,6 нм. Вычислите наибольшую длину волны в серии Бальмера.
611.Фотон с энергией 16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость будет иметь электрон вдали от ядра атома?
612.Найдите энергию и потенциал ионизации ионов He+ и Li++ .
613.Вычислите частоты вращения электрона в атоме водорода на второй и третьей орбитах. Сравните эти частоты с частотой излучения при переходе электрона с третьей на вторую орбиту.
614.Атом водорода переведен из нормального состояния в возбужденное, характеризуемое главным квантовым числом 2. Найдите энергию, необходимую для перевода атома водорода в указанное возбужденное состояние.
615.Какую работу нужно совершить, чтобы удалить электрон со второй орбиты атома водорода за пределы притяжения его ядром?
616.При переходе электрона водородного атома с одной из возможных орбит на другую, более близкую к ядру, энергия атома уменьшается на 1,892 эВ. Определите длину волны излучения.
617.Атом водорода излучает фотон частотой ν. Найдите изменение длины волны фотона, возникающее вследствие отдачи, претерпеваемой атомом при излучении.
58
618.Электрон в атоме водорода находится на третьем энергетическом уровне. Определите кинетическую, потенциальную и полную энергию электрона. Ответ выразите в электрон - вольтах.
619.Фотон выбивает из атома водорода, находящегося в основном состоянии, электрон с кинетической энергией 10 эВ. Определите энергию фотона.
620.На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны 435 нм?
621.При каком значении скорости длина волны де Бройля электрона равна ее комптоновской длине волны?
622.Определите кинетическую энергию электрона (в МэВ), при которой его дебройлевская и комптоновская длины волн равны между собой.
623.Средняя кинетическая энергия тепловых нейтронов близка к средней энергии атомов газа при комнатной температуре. Найдите длину волны де Бройля для таких нейтронов.
624.Найдите среднюю длину волны де Бройля теплового нейтрона, т.е. нейтрона, находящегося в тепловом равновесии с окружающей средой, при комнатной температуре.
625.Средняя кинетическая энергия электрона в невозбужденном атоме водорода равна 13,6 эВ. Вычислите дебройлевскую длину волны электрона.
626.Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 до 50 пм?
627.Найдите дебройлевскую длину волны молекул водорода, соответствующую их наиболее вероятной скорости при комнатной температуре.
628.Чему должна быть равна кинетическая энергия протона, чтобы дебройлевская длина волны совпадала с его комптоновской длиной волны?
629.Кинетическая энергия протона в три раза меньше его энергии покоя. Чему равна дебройлевская длина волны протона?
630.Вычислите дебройлевскую длину волны электрона, прошедшего ускоряющую разность потенциалов 511 кэВ.
631.При движении вдоль оси x скорость оказывается неопределенной с точностью
∆vx = 1 см/с. Оцените неопределенность координаты ∆x: а) для электрона; б) для броуновской частицы массы m = 10 -13 г; в) для дробинки массы 0,1г.
632.Определите: а) скорость, с которой электрон движется по первой боровской орбите в атоме водорода; б) исходя из того, что радиус атома имеет величину порядка 0,1 нм, оцените скорость движения электрона в атоме водорода из соотношения неопределенностей. Сравните это значение скорости со скоростью в пункте а).
633.Положение центра шарика массой 1 г и положение электрона определены с
ошибкой ∆x ~ 10-5 см. Какова будет неопределенность в скорости ∆vx для шарика и электрона?
634.Молекулы водорода участвуют в тепловом движении при температуре 300К. Найдите неопределенность координаты молекул водорода.
635.Длительность возбужденного состояния атома водорода соответствует примерно
10-7 с. Какова неопределенность энергии в этом состоянии? Ответ выразите в эВ.
636.Время жизни нейтрального пиона равно 8 10-17 с. С какой точностью может быть определена его масса?
59
637.Оцените наименьшие ошибки, с которыми можно определить скорость шарика массой 10-6 кг и электрона, если положение центра шарика и положение электрона установлены с точностью 10-6 м.
638.Средний промежуток времени между возбуждением атома и освобождением энергии составляет 10-8 с. Какова при этом неопределенность в энергии фотона и неопределенность в частоте света?
639.Длину волны можно определить с точностью 10-6. Чему равна неопределенность в положении рентгеновского кванта длиной волны 10-10 м при одновременном измерении его длины волны?
640.Среднее время жизни возбужденного состояния атома равно τ=12нс. Определите минимальную неопределенность длины волны λ= 0,12 мкм излучения при переходе атома в основное состояние.
641.Оцените долю электронов в меди, которые при ее нагревании до 100° С выйдут за пределы уровня Ферми.
642.Сравните электропроводность чистого германия при - 40° С и +100°С. Энергия активации для германия 0,72 эВ.
643.Во сколько раз изменится электропроводность чистого беспримесного
полупроводника при повышении температуры от - 23° С до +27° С. Ширина запрещенной зоны для этого полупроводника равна 0,74 эВ?
644.Найдите энергию Ферми для свободных электронов калия при абсолютном нуле. Считать, что на один атом приходится один свободный электрон.
645.Концентрация свободных электронов натрия 3 1028 м-3. Найдите скорость электронов на уровне Ферми при абсолютном нуле температуры.
646.Германиевый кристалл, ширина запрещенной зоны которого 0,72эВ, нагревают
от 0° С до 15° С. Во сколько раз возрастает его удельная электропроводность?
647.При нагревании кремниевого кристалла от 0° С до 10° С его электропроводность возрастает в 2,3 раза. Определите ширину запрещенной зоны кристалла кремния.
648.Найдите минимальную энергию, необходимую для образования пары электрон - дырка в кристалле CaAs, если его удельная проводимость изменяется в 10 раз при
изменении температуры от 20°С до 3° С.
649.Найдите минимальную энергию, необходимую для образования пары электрон - дырка в чистом теллуре, если известно, что его электропроводность возрастает в 5,2 раза при увеличении температуры от 300 К до 400 К.
650.Минимальная энергия образования пары электрон - дырка в чистом беспримесном полупроводнике 0,4 эВ. Во сколько раз изменится удельная электропроводность этого полупроводника при изменении температуры от 250К до
350К?
651.Найдите энергию связи ядра, которое имеет одинаковое число протонов и нейтронов и радиус, в полтора раза меньший радиуса ядра Al27.
652.Найдите с помощью табличных значений масс атомов: а) среднюю энергию
связи на один нуклон в ядре O16; б) энергию связи нейтрона и альфа - частицы в ядре
B11.
653. Найдите с помощью табличных значений масс атомов: а) энергию связи нейтрона и альфа - частицы в ядре B11; б) энергию, необходимую для разделения ядра O16 на четыре одинаковые частицы.
60
654. Найдите разность энергий связи нейтрона и протона в ядре B11. Объясните причину их различия.
655. Вычислите энергию, необходимую для разделения ядра Ne20 на две альфачастицы и ядро C12, если известно, что энергия связи на один нуклон в ядрах Ne20, He4, C12 равны, соответственно: 8,03; 7,07 и 7,68 МэВ.
656. Определите удельную энергию связи (в МэВ) ядер бора 5B11 и неона 10Ne20.
657. Определите удельную энергию связи (в МэВ) для ядер кремния 14Si28 и железа
26Fe56.
658. Определите удельную энергию связи (в МэВ) для ядер цинка 30Zn68 и бария
56Ba137.
659. Определите энергию связи (в МэВ), приходящуюся на один нуклон для ядер
82Pb207 и 92U235.
660. Определите энергию связи (в МэВ), приходящуюся на один нуклон для ядер
26Fe56 и 82Pb207.
661.Вследствие радиоактивного распада 92U238 превращается в 82Pb206. Сколько альфа- и бетапревращений он при этом испытывает? Напишите схему реакции распада.
662.За какое время распадается 87,5 % атомов 20Ca45 ?
663.Какая доля первоначального количества радиоактивного изотопа распадается за время жизни этого изотопа?
664.Сколько атомов 86Rn222 распадается за сутки в 1 г этого изотопа ?
665.Найдите период полураспада радиоактивного препарата, если за сутки его активность уменьшается в три раза?
666.Определите постоянную распада и период полураспада радона, если известно, что число атомов радона уменьшается за 1 сутки на 18,2 %.
667.Сколько атомов полония распадается за 1 сутки из 106 атомов? Период полураспада полония 138 суток.
668.Некоторый радиоактивный изотоп имеет постоянную распада 4 10-7 с-1. Через какое время распадается 75 % первоначальной массы атомов ?
669.Какое количество теплоты выделяется при распаде радона активностью 3,7 1010 Бк: а) за время 1 час; б) за среднее время жизни? Кинетическая энергия вылетающей из радона альфа - частицы 5,5 МэВ. Напишите схему распада.
670.При радиоактивном распаде радия образуется радон. Напишите схему распада. Найдите активность радона, образовавшегося из 1 г радия за время 1 час.
671.Вычислите энергии ядерных реакций:
1)n + 5B10 -> 3Li7 + 2He4;
2)p + 5B11 -> 3 2He4.
672. Вычислите энергии ядерных реакций:
1) 1H2 + 1H3 -> 2He4 + n; 2) 2He4 + 7N14 -> 8O17 + p.
673. Определите энергию, которая освобождается при термоядерной реакции: 3Li6 +
1H2 -> 2 2He4.
Расчет произвести на ядро и на один нуклон. Сравните с энергией, выделяемой при делении урана.
