Банк задач для подготовки к экзамену по дисциплине

Математический анализ

ИВТ

2 семестр

Модуль 1 – Дифференцирование функции одной переменной.

1. Найти область определения функции .

2. Найдите период функции 1. 2. 3.

3. Найти образ отрезка  при отображении  .

4. Какие из функций являются периодическими

5. Найти множество значений функции  

6. Даны множества А и В. Что представляет собой множество С, изображенное на рисунке,

Теория пределов.

7. Найти -окрестность точки М(3), если .

8. Вычислить пределы.

9. 

10. 

11. 

12. 

13. 

Производная.

Найти :

14. ;

15. ;

16. ;

17. ;

18. .

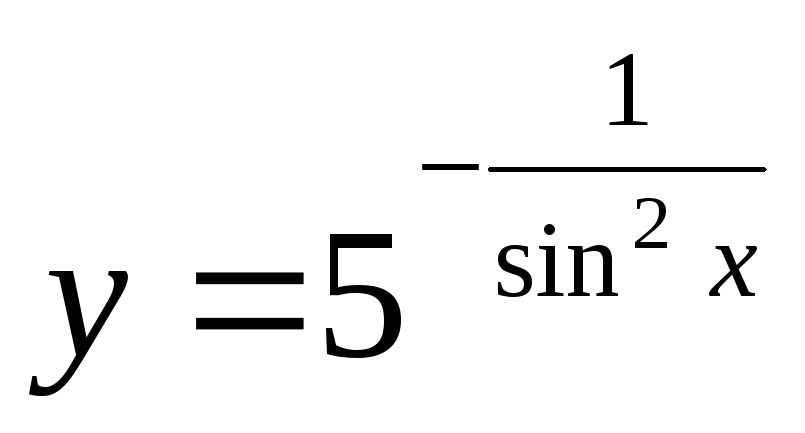Найти :

19. .

Найти :

20. .

Найти :

21. 

22. Исследовать функции на экстремум, выпуклость, вогнутость, асимптоты и построить график:

а) б)

в) г) .

23. Найти асимптоты (горизонтальную и вертик-ную) графика функции  .

24. Найти кривизну и радиус кривизны линии в точке .

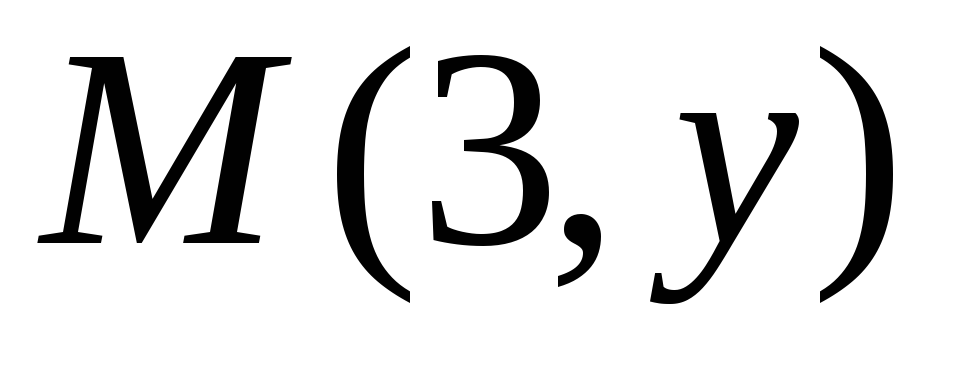Модуль 2 – Интегрирование функции одной переменной.

25. Вычислить Неопределенный интеграл:

1. 8)

2. 9)

3. 10)

4. 11)

5. 12)

6. 13)

7. 14)

15)

В п. 2, 4, 6, 7, 14, 15 сделать проверку дифференцированием.

26. Вычислить Определенный интеграл:

Вычислить:

1. 4)

2. 5)

3. 6)

7. 9)

8. 10)

27. Исследовать сходимость несобственного интеграла:

1. 4)

2. 5)

3. 

28. Найти площадь области, ограниченной линиями:

1)

2)

3)

4) (в полярных координатах)

5)

6)

7)

8. 

29. Найти длину дуги кривой:

1)

2)

3)

4)

5)

6)

30. Найти объем тела, образованного вращением фигуры, ограниченной линиями:

1) вокруг ОХ

2) , вокруг ОУ

3) , вокруг ОХ

4. , , вокруг ОУ

31. Вычислить приближенное значение интеграла методами прямоугольников, трапеций и Симпсона, разбив промежуток интегрирования на 10 равных частей.

Модуль 3 – Дифференциальные уравнения.

32. Найти общее решение уравнения:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

33. Решить задачу Коши:

1)

2)

3)

4)

5) ,

6)

34. Методом Эйлера найти значение решения дифференциального уравнения для которого y(2)=1, в пяти точках отрезка [2;2,5], приняв h=0,1.

– Дифференцирование функции нескольких переменных.

35. Построить графики функций двух переменных (метод главных сечений):

1. 

2. 

3. 

4. 

5. 

36. Найти :

1. 

2. 

3. 

4. 

5. 

37. . Доказать, что

38. Доказать, что

39. Найти все частные производные 2-го порядка:

1. 

2. 

3. 

40. Найти из уравнений:

1. 

2. 

41. Найти из уравнений:

1. 

2. 

42. Доказать, что если

43. Найти градиент функции:

1. в т.

2. 

3. в т.

4. 

5. в т.

44. Найти экстремум функции:

1. 

2.