Разделяем переменные:

Переходим теперь к первоначальной функции у и переменной х.

Итого, выражение является общим интегралом исходного дифференциального уравнения.

3.8 Решить уравнение

Решение: Полагаем, тогда, т. е.. Сначала решаем уравнениеТеперь решаем уравнение, т.е.. Итак, общее решение данного уравнения есть, т.е.

3.9 Решить уравнение.

Решение: Полагаем, тогда, т. е.. Сначала решаем уравнениеТеперь решаем уравнение, т.е.. Итак, общее решение данного уравнения есть

3.10 Решить уравнение

Решение:Проверим условие

Условие выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.

Определим функцию u.

;

Итого,

Находим общий интеграл исходного дифференциального уравнения:

3.11Решить уравнениес начальными условиямиx₀ = 0; y₀ = 1;

Решение:

Подставим начальные условия:

Получаем частное решение (решение задачи Коши): .

3.12 Найти общее решение уравнения.

Решение:Применяем подстановку

Произведя обратную замену, получаем:

Общее решение исходного дифференциального уравнения:

3.13 Найти общее решение уравнения

Решение: Замена переменной:

1)

Для решения полученного дифференциального уравнения произведем замену переменной:

С учетом того, что , получаем:

Общий интеграл имеет вид:

2)

Таким образом, получили два общих решения.

3.14 Решить уравнение.

Решение: Составим характеристическое уравнение:

Общее решение имеет вид:

3.15 Решить уравнение

Решение:Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое - либо частное решение.

Таким частным решением будет являться функция

Исходное дифференциальное уравнение можно преобразовать:

Общее решение имеет вид:

Окончательно:

3.16 Решить уравнение

Решение:Характеристическое уравнение:

Общее решение:

3.17 Решить уравнение

Решение:Характеристическое уравнение:

Общее решение:

3.18 Решить уравнение

Решение:Характеристическое уравнение:

Общее решение:

3.19Решить уравнение

Решение:Характеристическое уравнение:

Общее решение:

3.20 Решить уравнение

Решение:Решаем линейное однородное уравнение

Решение неоднородного уравнения будет иметь вид:

Составляем систему уравнений:

Решим эту систему:

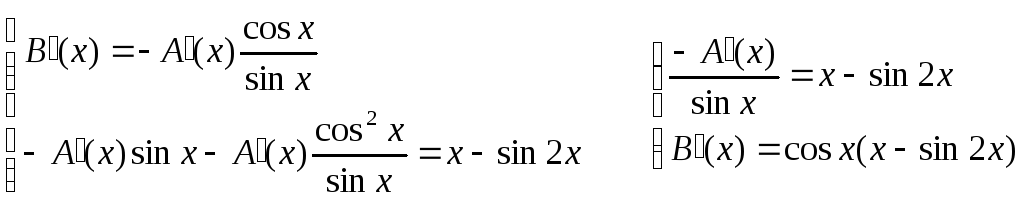
Из соотношения найдем функциюА(х).

Теперь находим В(х).

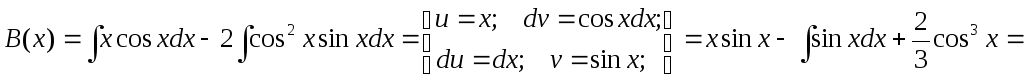
Подставляем полученные значения в формулу общего решения неоднородного уравнения:

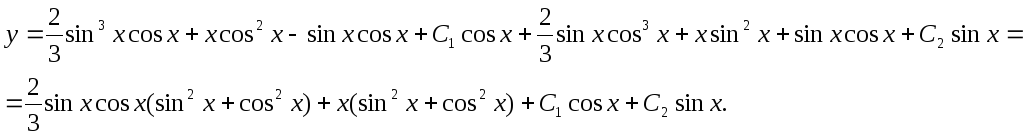Окончательный ответ:

3.21 Решить уравнение.

Решение:Решим соответствующее однородное уравнение:

Теперь найдем частное решение исходного неоднородного уравнения.

Сопоставим правую часть уравнения с видом правой части

Частное решение ищем в виде: , где

Т.е.

Теперь определим неизвестные коэффициенты А и В.

Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.

Итого, частное решение:

Тогда общее решение линейного неоднородного дифференциального уравнения:

3.22 Решить уравнение

Решение:

Правую часть дифференциального уравнения представим в виде суммы двух функций f₁(x) + f₂(x) = x + (-sinx).

Составим и решим характеристическое уравнение:

Для функции f₁(x) =х()решение ищем в виде .

Получаем: Т.е.

Итого:

Для функции f₂(x) =-sinx () решение ищем в виде: .

Анализируя функцию f₂(x), получаем:

Таким образом,

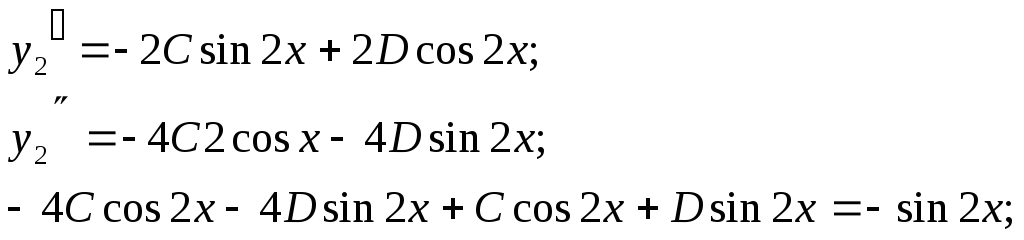
Итого:

Т.е. искомое частное решение имеет вид:

Общее решение неоднородного дифференциального уравнения:

3.23Решить уравнение

Решение:

Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:

Общее решение однородного уравнения:

Теперь найдем частное решение неоднородного уравнения в виде:

Воспользуемся методом неопределенных коэффициентов.

Подставляя в исходное уравнение, получаем:

Частное решение имеет вид:

Общее решение линейного неоднородного уравнения:

3.24 Решить уравнение

Решение:

Характеристическое уравнение:

Общее решение однородного уравнения:

Частное решение неоднородного уравнения: .

Находим производные и подставляем их в исходное неоднородное уравнение:

Получаем общее решение неоднородного дифференциального уравнения:

3.25 Найти общее решение системы уравнений:

Решение:Составим характеристическое уравнение:

Решим систему уравнений:

Для k₁:

Полагая (принимается любое значение), получаем:

Для k₂:

Полагая (принимается любое значение), получаем:

Общее решение системы:

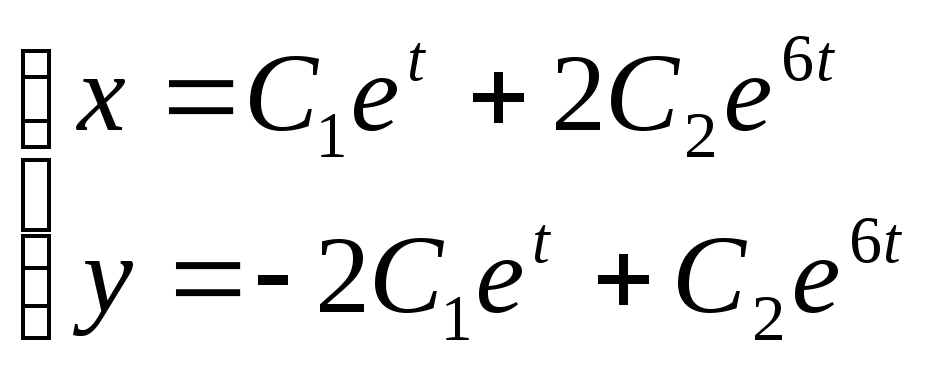
3.26 Найти решение системы уравнений

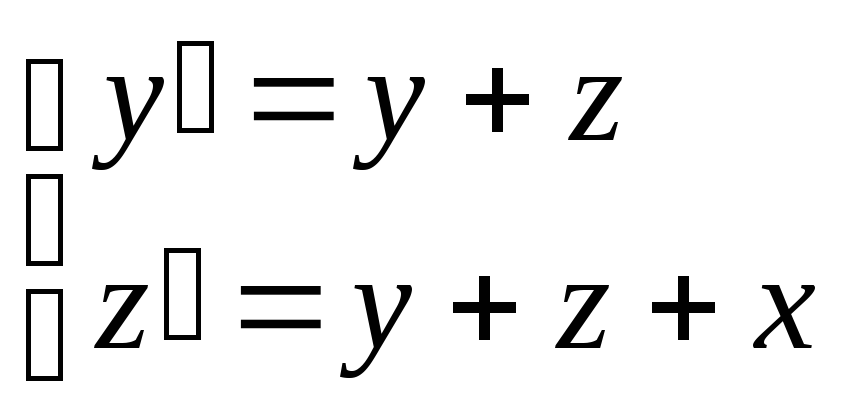
Решение:Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т.к. не является однородным (в уравнение входит независимая переменнаях).

Для решения продифференцируем первое уравнение по х. Получаем:

Заменяя значение z’из второго уравнения получаем: .

С учетом первого уравнения, получаем:

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения:

Теперь находим частное решение неоднородного дифференциального уравнения по формуле

Общее решение неоднородного уравнения:

Подставив полученное значение в первое уравнение системы, получаем:

3.27 Найти решение системы уравнений:

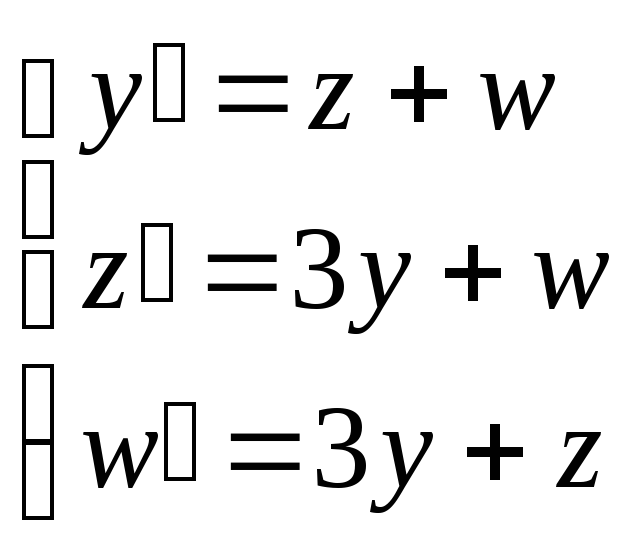
Решение:Составим характеристическое уравнение:

1. k = -1.

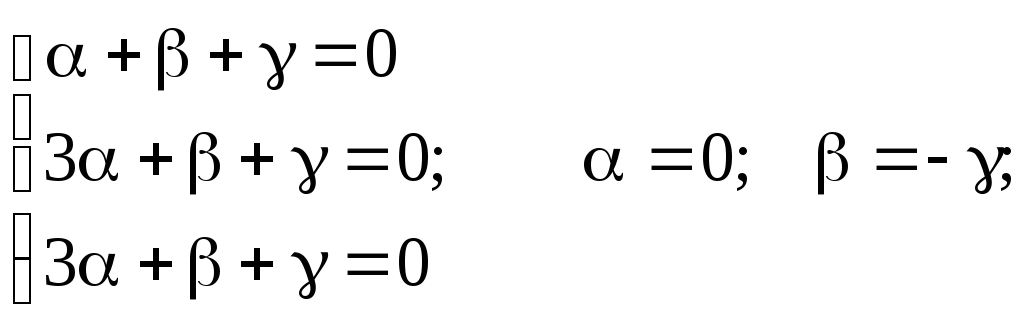
Если принять = 1, то решения в этом случае получаем:

2. k₂ = -2.

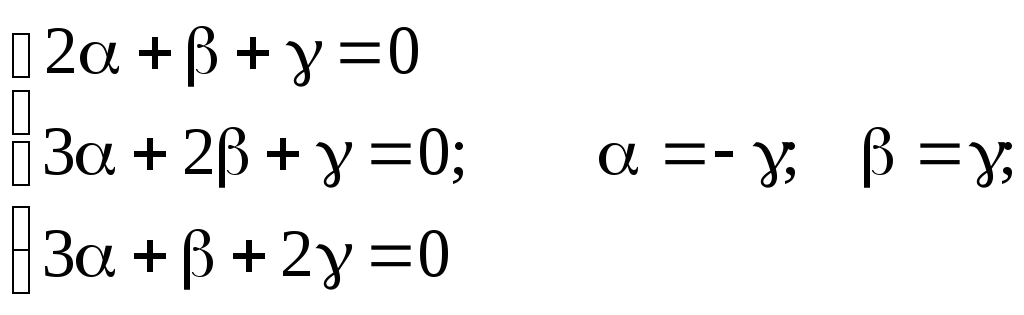
Если принять = 1, то получаем:

3. k₃ = 3.

Если принять = 3, то получаем:

Общее решение имеет вид: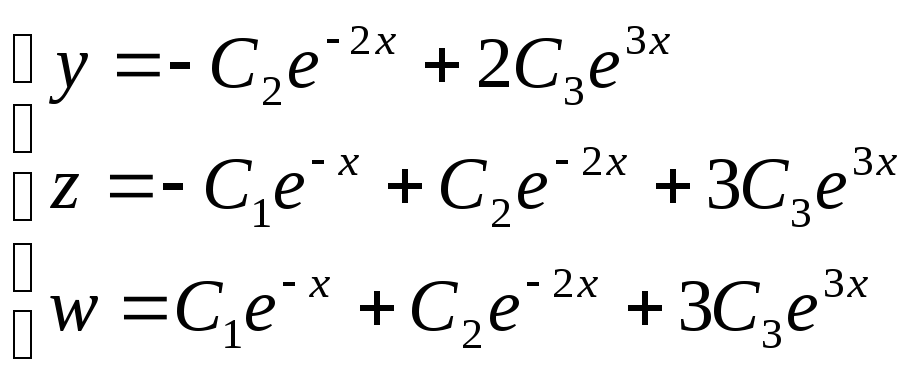

3.28Методом Эйлера найти значение решения дифференциального уравнениядля которогоy(1)=1, в пяти точках отрезка [1;1,5], принявh=0,1.

По формулам

находим точки Значение искомой функцииy=y(x), удовлетворяющей условию данной задачи Коши, вычисляем по формуле

(k = 0, 1, 2, …, n).

Результаты вычислений занесены в таблицу 1.

Таблица 1

k
0	1,0000	1,0	1,0	1,0000	0,1000	1,1000
1	1,1000	1,1	2,2	1,1000	0,1100	1,2100
2	1,2100	1,2	2,4	1,9000	0,1190	1,3290
3	1,3290	1,3	2,6	1,2710	0,1271	1,4561
4	1,4561	1,4	2,8	1,3439	0,1344	1,5905
5	1,5905	1,5	3,0	1,4095	0,1410	1,7315

Ряды.

3.29 Написать пять первых членов ряда по данному общему члену.

Решение. Полагая , получаем. Если, тои далее (при),,. Следовательно,

3.30 Написать формулу общего члена для ряда

Решение. Знаменатели членов данного ряда – квадраты натуральных чисел, следовательно, общий член ряда

.

3.3 Найти для ряда частичную сумму первых n членов (S_n); показать, пользуясь определением, сходимость (расходимость) ряда; найти сумму ряда (S):

Решение. Общий член ряда запишем иначе:

.

Определяя коэффициенты А и В, получаем .

Следовательно, .

Напишем частичную сумму ряда

.

,

отсюда следует, что ряд сходится и его сумма S=1.

3.31 Исследовать сходимость ряда

Решение: Найдем 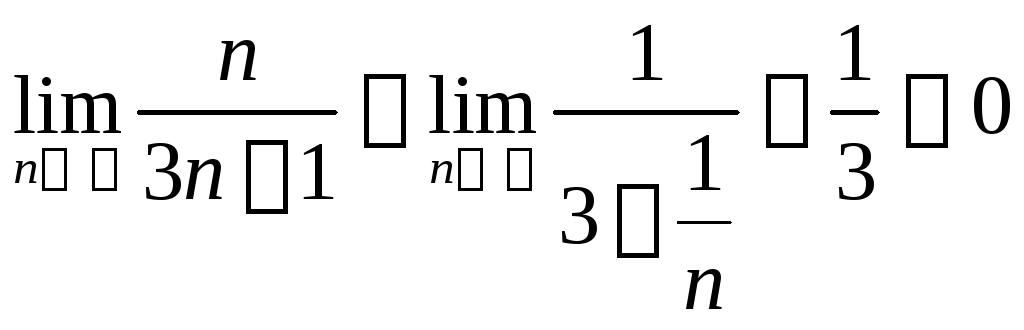- необходимый признак сходимости не выполняется, значит ряд расходится.

3.32 Исследовать на сходимость ряд

Решение: Т.к. , а гармонический рядрасходится, то расходится и ряд.

3.33 Исследовать на сходимость ряд

Решение: Т.к. , а рядсходится ( как убывающая геометрическая прогрессия), то рядтоже сходится.

3.34 Определить сходимость ряда .

Решение: Используем признак Даламбера

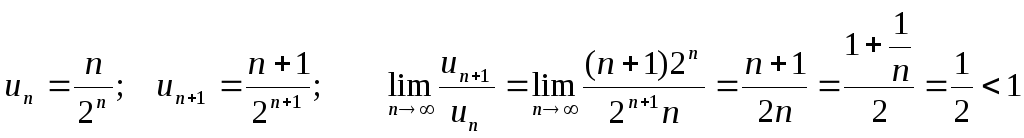
ряд сходится.

3.35 Определить сходимость ряда

Решение: Используем признак Даламбера

ряд сходится.

3.36 Определить сходимость ряда .

Решение: Используем признак Коши

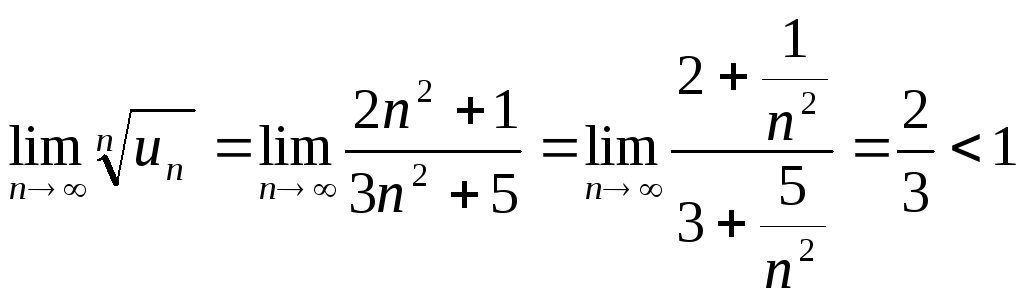
ряд сходится.

3.37 Исследовать по интегральному признаку Коши сходимость ряда:

.

Решение. Пусть y=–непрерывная, монотонно убывающая и принимающая только положительные значения в интервале (0,) функция, причем ее значения, отвечающие целым положительным числам 1, 2, 3,…, совпадают с соответствующими членамиданного ряда. Найдем несобственный интеграл

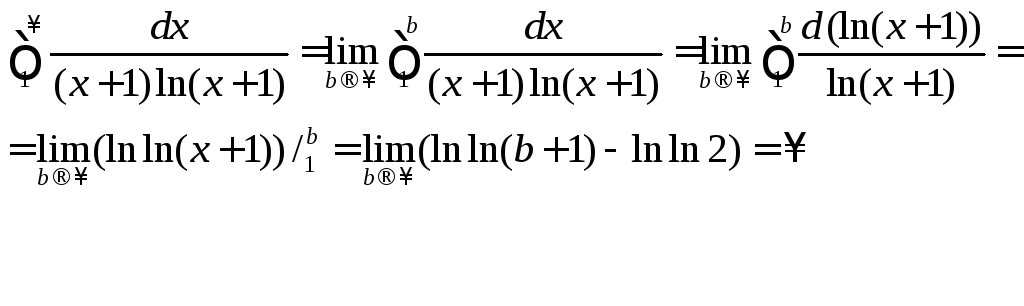
Несобственный интеграл расходится, следовательно, по интегральному признаку данный ряд тоже расходится.

3.38 Исследовать сходимость знакопеременных рядов:

1); 2); 3).

Решение. 1) Члены данного ряда убывают по абсолютной величине, знаки чередуются и общий член с возрастанием n стремится к нулю. Поэтому, согласно признаку Лейбница, ряд 1 сходится. Ряд, составленный из абсолютных величин членов данного ряда

,

есть гармонический ряд, который, как уже известно, расходится. Следовательно, ряд 1 сходится условно.

2) Члены данного знакочередующегося ряда убывают по абсолютной величине, однако общий член не стремится к нулю с возрастанием n, , т. е. необходимое условие сходимости ряда не выполнено, поэтому ряд 2 расходится.

3) Составим ряд из абсолютных величин данного знакопеременного ряда

(в)

Сравним ряд (в) со сходящимся рядом

(г)

Каждый член ряда (в) не превосходит соответствующего члена ряда (г), поэтому, согласно признаку сравнения, ряд (в) сходится. Следовательно, данный ряд 3 сходится абсолютно (безусловно).

3.39 Исследовать на сходимость ряд

Решение: Применяем признак Даламбера:

.

Получаем, что этот ряд сходится при и расходится при.

Теперь определим сходимость в граничных точках 1 и –1.

При х = 1: ряд сходится по признаку Лейбница

При х = -1: ряд расходится (гармонический ряд).

3.40 Найти область сходимости рядов:

1) ; 2).

Решение. 1) . Ряд сходится только в одной точкеx=0.

2) Положив в данном ряду x-1 =y, получим ряд

. (a)

Найдем радиус сходимости этого ряда:

. Исследуем поведение ряда на концах интервала . Пустьy=, тогда получим расходящийся ряд . Пустьy=, тогда получим ряд, который также расходится. Следовательно, ряд (а) сходится в интервале. Заменив переменнуюy через переменную x, получим искомую область сходимости данного ряда:

или .