Физика / Физика / Механика. Лекции / lekcii_meh / glava2
.pdf
Решение. Из второго закона Ньютона
R
FR = dp dt
выразим изменение импульса точки
R |
= Fdt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для того, чтобы найти изменение импульса точки за промежуток времени |
|||||||||||||||||||||
от 0 до t |
проинтегрируем правую часть равенства в указанных пределах, а левую |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
||
– от начального импульса p0 до конечного – |
p |
|
|
|
|
||||||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
R |
|
|
t |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= ∫Fdt . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫dp |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
R |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставив вместо F соответствующее выражение, и проинтегрировав обе части |
|||||||||||||||||||||
равенства, получим |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
R R |
|
|
|
t |
R |
|
R |
|
R |
|
R t |
R t |
|
R t |
t2 R |
R |
R |
||||
p - p0 = ∫(ti |
+ 3t2 j |
+ 2k)dt = i ∫tdt + j∫ |
3t2dt + k∫2dt = |
|
i + t3 j + 2tk . |
||||||||||||||||
2 |
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
0 |
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из этого равенства выразим конечный импульс материальной точки |
|
||||||||||||||||||||
R |
|
t |
2 R |
|
R |
R |
R |
t2 R |
R |
|
R |
|
|
|
|
||||||
p = |
|
|
|
|
i |
+ t3 j |
+ 2tk |
+ p0 = |
|
i + (t3 + |
2)j |
+ |
(2t - 0,5)k . |
|
|
|
|
||||
2 |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставим числовое значение времени и получим вектор конечного импульса |
|||||||||||||||||||||
R |
12 R |
|
|
R |
|
|
|
R |
R |
R |
R |
|
|
|
|
||||||
p = |
|
|
|
|
i |
+ (13 + 2)j + (2 ×1- 0,5)k = 0,5i + 3j |
+1,5k . |
|
|
|
|
||||||||||
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Модуль вектора p найдем из равенства |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
p = |
|
|
|
px2 + py2 + pz2 = 0,52 + 32 +1,52 |
= 3,4 Н×с. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R R |
|
Задача 2. |
|
|
|
|
|
m1 = 2 кг , летящий со скоростью |
= 3i + 2j - k |
||||||||||||||
Шар массой |
v1 |
||||||||||||||||||||
(м/с), испытывает абсолютно неупругое соударение с шаром массой m2 = 3 кг,
R |
R |
R |
|
= -2i |
+ 2j + 4k (м/с). Определите |
||
имеющим в момент соударения скорость v2 |
вектор скорости v шаров и его модуль v после удара.
Решение. Запишем закон сохранения импульса для
неупругого соударения
m1v1 + m2 v2 = (m1 + m2 )v .
Из этого равенства выразим вектор скорости шаров после соударения
|
R |
R |
|
R |
m1v1 |
+ m2v2 |
|
v = |
|
|
|
(m1 |
+ m2 ) |
||
|
и, подставив числовые значения, получим
|
R |
R |
- k) + 3 |
R |
R |
+ 4k) |
|
|
R |
2 ×(3i |
+ 2j |
×(-2i |
+ 2j |
R |
R |
||
v = |
|
|
|
|
|
|
= 2j |
+ 2k . |
|
|
2 + |
3 |
|
|
|||
|
|
|
|
|
|
|
Модуль скорости шаров после удара найдем по формуле
v = 
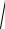vx2 + vy2 + vz2 = 
02 + 22 + 22 » 2,8 м/с.
§ 8
Уравнение движения тела переменной массы
Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается за счет истечения газов, образующихся при сгорании
топлива, и т.п.
Выведем уравнение движения тела переменной массы на примере движения
ракеты. Если в момент времени t масса ракеты m , а ее скорость v, то по истече-
нию времени dt , ее масса уменьшится на dm и станет равной m - dm , а ско-
|
R |
R |
|
|
рость станет равной v + dv . Изменение импульса системы за отрезок времени dt |
||||
dp = [(m - dm)(v + dv)+ dm(v + u)]- mv, |
||||
R |
R |
R |
R R |
R |
где u – скорость истечения газов относительно ракеты. Тогда |
||||
R |
R R |
|
|
|
dp = mdv + udm |
|
|
|
|
|
R |
малый член высшего порядка малости по сравнению с ос- |
(учли, что dm × dv – |
||
тальными). |
|
|
|
|
R |
Если на систему действуют внешние силы, то dp = F × dt , поэтому |
||
R |
R |
|
Fdt = mdv |
+ udm , или |
|
|
|
R |
|
R |
R dm |
|
|
|
||
|
dv |
|
|
|
|
|||||
m |
|
|
= F − u |
|
. |
|
(8.1) |
|||
dt |
dt |
|
||||||||
|
|
|
|
|
|
|
||||
R dm |
|
|
|
|
|
|
||||
Член − u |
|
|
называют реактивной силой Fp |
. Если |
u противоположен v, то ра- |
|||||
dt |
||||||||||
|
|
|
|
|
|
|
|
|||
кета ускоряется, а если совпадает с v, то тормозится. |
|
|||||||||
Таким образом, мы получили уравнение движения тела переменной массы |
||||||||||
|
R |
|
|
|
|
|
|
(8.2) |
||
ma = F + Fp , |
|
|
||||||||
которое впервые было выведено И.В. Мещерским (1859–1935 гг).
Идея применения реактивной силы для создания летательных аппаратов высказывалась в 1881 г. Н.И. Кибальчичем (1854–1881 гг). К.Э. Циолковский
(1857–1935) в 1903 г. опубликовал статью, где предложил теорию движения раке-
ты и основы теории жидкостного реактивного двигателя. Поэтому его считают основателем отечественной космонавтики.
Применим уравнение (8.1) к движению ракеты, на которую не действуют никакие внешние силы. Полагая F = 0 и считая, что скорость выбрасываемых га-
зов относительно ракеты постоянна (ракета движется прямолинейно), получим
m dv = −u dm , dt dt
откуда
v = −u∫ dmm = −uln m + C.
Значение постоянной интегрирования C определяем из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса m0 , то C = uln m0 . Следовательно
v = uln |
m0 |
. |
(8.3) |
|
|||
|
m |
|
|
Это соотношение называется формулой Циолковского. Оно показывает что:
1) чем больше конечная масса ракеты m , тем больше должна быть стартовая мас-
са ракеты m0 ;
2) чем больше скорость истечения u газов, тем больше может быть конечная мас-
са при данной стартовой массе ракеты.
Выражения (8.2) и (8.3) получены для нерелятивистских движений, т.е. для случаев, когда скорости v, u << c ( c – скорость света в вакууме).
Задача 1. На катере массой m = 5 т находится водомет, выбрасывающий
μ = 25 кг/с воды со скоростью u = 7 м/с относительно катера назад. Пренебрегая сопротивлением движению катера, определите: 1) скорость катера через 3 мин после начала движения; 2) предельно возможную скорость катера.
Решение. Запишем уравнение движения для катера в векторном виде
|
R |
R |
|
|
|
dv |
|
|
|
m |
= F , |
|
||
|
|
|||
|
dt |
|
|
|
|
|
R |
R |
реактивная сила, действующая на катер со стороны выбрасы- |
где F = −μ(u + v) – |
||||
ваемой воды; |
u + v – скорость выбрасываемой воды относительно неподвижной |
|||
системы отсчета (например, берега). Подставив выражение для силы в уравнение движения, получим
|
R |
|
|
|
dv |
R R |
|
m |
|
= −μ(u + v) . |
|
dt |
|||
|
|
Перейдем от векторной формы уравнения движения к скалярной с учетом на-
правления оси x
mdv = −μ(v − u) . dt
Переменными в данном дифференциальном уравнении являются скорость v и
время t . Это уравнение будем решать методом разделения переменных
dv |
= − |
μ |
dt . |
v − u |
|
||
|
m |
||
Проинтегрируем обе части этого равенства
v |
dv |
= − |
μ |
t |
|
∫ |
∫ dt , или |
||||
v − u |
m |
||||
0 |
|
0 |
|||
|
|
|
v - u = - m ln t .- u m
Выразим из полученного равенства скорость катера
− μ t
v = u 1- e m
.
Подставим числовые значения в СИ и найдем скорость катера в указанный момент времени
|
|
|
− |
25 |
180 |
|
|
|
|
|
|
||||
v = 7 × |
|
- e |
5000 |
|
|
= 4,15 м/с. |
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
Из равенства для скорости видно, что максимальное значение скорости ка-
тера достигается при t → ∞ , и это значение будет равно vmax = 7 м/с.