4.4 Численное решение обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши. Найти решение обыкновенного дифференциального уравнения

y = f (x, y),

на отрезке [a, b], (x₀ = a), удовлетворяющее начальному условию y(x₀) = y₀. При численном решении поставленной задачи отрезок [a,b] разбивают на n (не обязательно равных) частей и определяют приближенные значения искомой функции y (x) в точках деления x_i (y_i = y (x_i)).

4.4.1. Метод Эйлера. Геометрический смысл решения методом Эйлера (методом Рунге-Кутта первого порядка) состоит в том, что на малом отрезке (x_i, x_i + h) интегральная кривая y = y (x) дифференциального уравнения заменяется отрезком ее касательной в точке (x_i; y_i). Приближенное значение в точке x_i+1 = x_i + h находится по формуле:

y_i+1 = y_i + h  y (x_i) = y_i + h  f (x_i, y_i).

y

Рисунок 4.10 - Геометрическая интерпретация метода Эйлера

Блок-схема алгоритма метода Эйлера представлена в Приложении 6.

Пример. Найти решение дифференциального уравнения y = sin(xy) на отрезке [0, 0.5] при начальном условии y(0) = 2 и числе разбиений отрезка n=5.

Решение. При разбиении отрезка на 5 частей шаг постоянный h = 0,1. Начальное условие задачи x₀ = 0, y₀ = 2. Тогда при x₁ = 0,1 значение y₁ = y (x₁) = y₀ + h sin(x₀y₀), т.е. y₁ = 2 + 0,1sin(02) = 2. В точке x₂ = 0,2 значение y₂ = y₁ + h f(x₁y₁) = 2 + 0,1sin(0,12) = 2,019. Продолжая вычисления по формуле Эйлера, получим:

x₃ = 0,3; y₃ = 2,019 + 0,1sin(0,22,019) = 2,058

x₄ = 0,4; y₄ = 2,058 + 0,1sin(0,32,058) = 2,116

x₅ = 0,5; y₅ = 2,116 + 0,1sin(0,42,116) = 2,191

Решение этой задачи будет тем точнее, чем меньше шаг деления отрезка h.

4.4.2. Метод Рунге-Кутта (четвертого порядка). Рассматриваемый метод получил наиболее широкое распространение в практических расчетах. Его погрешность оценивается величиной ε  h⁵, что дает возможность получить более точные результаты, чем в методе Эйлера. Не давая полного описания вывода формул, приведем их в следующем виде:

Здесь символом f (x, y), так же как и в описанном методе Эйлера, обозначается правая часть решаемого дифференциального уравнения, y_i+1 и y_i - приближенные значения интегральной функции в точках x_i+1 и x_i, h_i = x_i+1 - x_i. Блок-схема этого метода представлена в Приложении 6.

Замечание. Одним из недостатков метода является отсутствие простого способа оценки погрешности. Грубую оценку погрешности можно получить по формуле:

ε  y_h – y_h/2/ 15,

где y_h – значение, вычисленное с шагом h, y_h/2 - с шагом h / 2. Если полученные результаты удовлетворяют допустимой погрешности, в дальнейших расчетах шаг удваивают, иначе – уменьшают его вдвое. Приведенный способ приводит к необходимости дополнительных затрат времени счета на ЭВМ.

4.5 Математическая обработка данных

На практике часто приходится иметь дело с данными, полученными в результате измерений, наблюдений. Они обычно представлены в виде табличных зависимостей y_i = y (x_i), где y_i – значения результатов опыта, полученные для заданных величин x_i. В этих случаях обычно требуется найти аналитическую функцию y = f(x), которая наиболее точно отражает зависимость результатов измерений, и с ее помощью можно найти значение для любой точки x. Существует два подхода к решению поставленной задачи: а) функция должна точно проходить через узлы (x_i; y_i) – интерполяция и б) функция проходит с наименьшим отклонением от узлов и наиболее проста – аппроксимация.

4.5.1. Интерполяция. Задача интерполяции математически формулируется так: пусть на отрезке [a,b] заданы точки x₀, x₁, .. x_n, со своими значениями y₀, y₁, .. y_n. Требуется найти функцию y = f (x), которая в узлах интерполяции x_i принимает значения y_i, т.е. y_i = f (x_i). Решение этой задачи может быть выполнено двумя способами: локальной или полной интерполяцией.

Локальная интерполяция заключается в том, чтобы использовать только близлежащие точки. Например, если значение x лежит между x_i и x_i+1, то значение функции y = f (x) может быть найдено с помощью линейной интерполяции по формуле:

Более точный результат можно получить, если использовать информацию о трех близлежащих точках (квадратичная интерполяция). В этом случае можно однозначно определить коэффициенты параболы y_i = a_ix² + b_ix + c_i для любого отрезка [x_i-1; x_i+1], которому принадлежит x. Решение системы линейных уравнений вида

позволяет определить неизвестные коэффициенты a_i, b_i, c_i и значение y = a_ix² + b_ix + c_i. Блок-схема алгоритма квадратичной интерполяции представлена в Приложении 6.

Более точное значение y может быть получено с помощью интерполяционных многочленов, использующих информацию обо всех узлах функции. В качестве примера приведем формулу интерполяционного многочлена Лагранжа:

Пример. Для функции, заданной таблично

x	1	2	3	5
y	9	26	58	194

найти значение y в точке x=4 методами локальной линейной и квадратичной интерполяции, а также используя многочлен Лагранжа.

Решение. 1) Используя формулу локальной линейной интерполяции, получим: y = 58 + (194 - 58) (4 – 3)/(5 - 3) = 126.

2. Для квадратичной зависимости составим систему линейных уравнений:

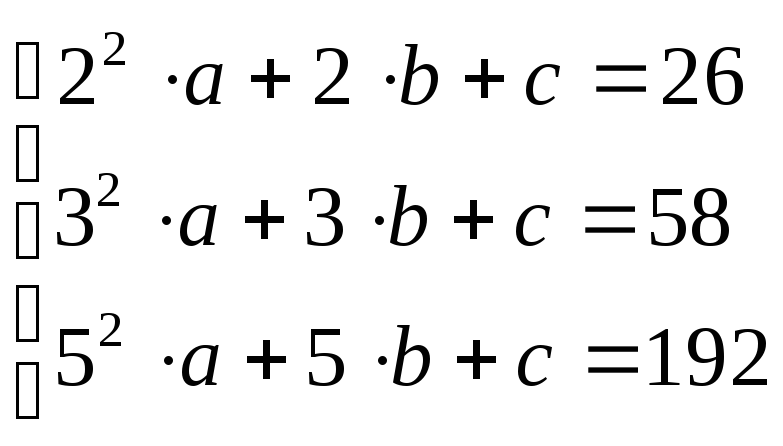
Решение этой системы дает значения a = 11,66; b = -26,33; c = 15. Таким образом y = 11,664² – 26,334 + 15 = 96,23.

2. Многочлен Лагранжа выглядит следующим образом:

Отметим, что последний результат наиболее точно соответствует данной зависимости.

4.5.2. Аппроксимация. Построение полного интерполяционного полинома требует определения его коэффициентов, число которых равно количеству заданных точек. При большом числе экспериментальных данных (x_i, y_i) хранение информации о коэффициентах также затруднительно, как и хранение самих данных. В этих случаях ставится вопрос о нахождении функции f (x, a₀, a₁, ... a_m), зависящей от параметров, число которых значительно меньше количества заданных точек (m<<n). Аппроксимирующая функция часто ищется в виде полинома

,

для нахождения коэффициентов которой используется следующий критерий:

должен принимать наименьшее значение (метод наименьших квадратов).

Необходимым условием минимума указанного критерия является равенство нулю всех частных производных функции F по параметрам a₀, a₁, ..., a_m (F/a_i = 0, i = 0, 1, ... m).

4.5.2.1. Линейное приближение методом наименьших квадратов. Пусть аппроксимирующая функция является линейной относительно x, т.е.

f(x, a₀, a₁) = a₀x + a₁.

В этом случае критерий принимает вид:

Условия минимума значения F (F / a₀ = 0, F / a₁ = 0) приводят к системе линейных уравнений:

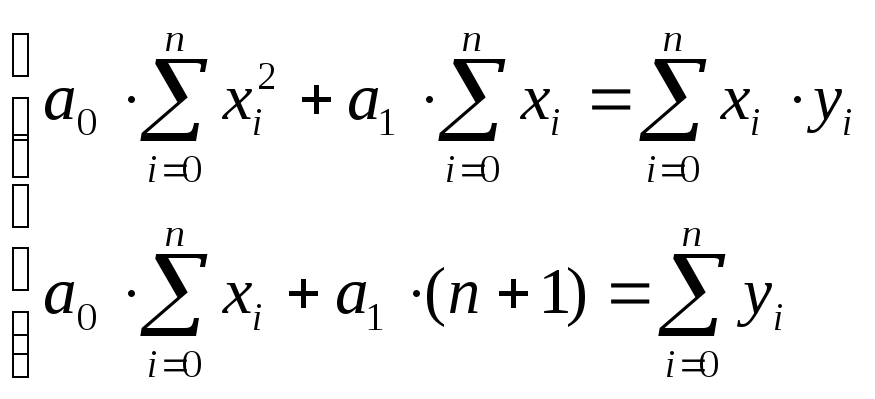
решение которой позволяет определить неизвестные параметры a₀ и a₁.

Пример. Определить линейную зависимость для функции, заданной таблично:

x	x1 = 1	x2 = 2	x3 = 3	x4 = 4	x5 = 5
y	5	6	10	11	13

Решение. Для определения неизвестных параметров функции y = a₀x + a₁ составим систему уравнений:

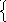55a₀ + 15a₁ = 156

15a₀ + 5a₁ = 45

Решение данной системы позволяет найти значения a₀ = 2,1, a₁ = 2,7 и указать линейную зависимость: y = 2,1x + 2,7.

4.5.2.2. Аппроксимация параболической зависимостью. Пусть искомая функция является квадратичной, т.е.

В этом случае критерий метода наименьших квадратов принимает вид:

и условия минимума значения F (F/a₀ = 0, F/a₁ = 0, F/a₂ = 0) приводят к системе трех линейных уравнений:

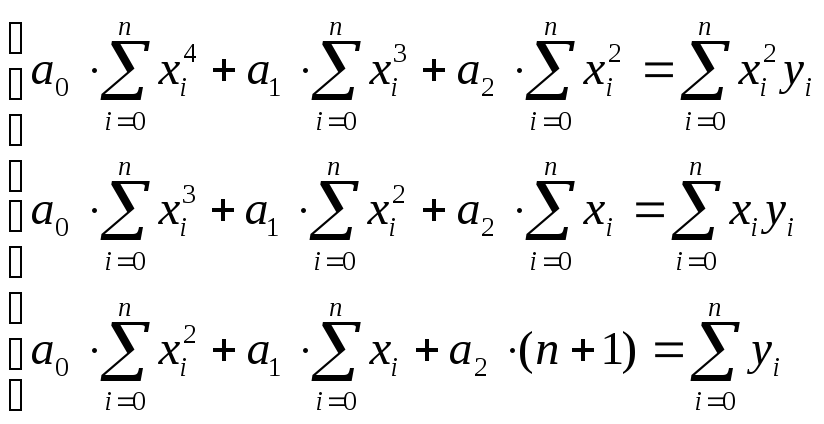
Решение данной системы позволяет найти неизвестные коэффициенты a₀, a₁, a₂ и определить функциональную зависимость. Блок-схема алгоритма определения неизвестных a₀, a₁, a₂ представлена в Приложении 6.