75

Глава 4 численные методы

С помощью математического моделирования постановка научно-технической задачи сводится к формулировке математической задачи, решение которой зачастую можно выполнить только методами вычислительной математики. Численный метод решения задачи – это определенная последовательность операций над числами, т.е. вычислительный алгоритм, язык которого – числа и арифметические действия. Такая примитивность языка позволяет реализовать численные методы на вычислительных машинах, что делает их мощным и универсальным инструментом исследования.

Некоторые из методов предлагаются для изучения в этой главе и требуются для выполнения контрольной работы №2.

4.1 Приближенное решение нелинейных уравнений

Всякое уравнение с одним неизвестным имеет вид:

f (x) = 0 или  (x) = g (x),

где f (x),  (x), g (x) – заданные функции, определенные на некотором числовом множестве X. Совокупность значений переменной X, при которых уравнение превратится в тождество, называется решением этого уравнения, а каждое значение X из этой совокупности – корнем уравнения. Нахождение корней уравнения с помощью точных аналитических формул выполняется в частных случаях. В большинстве практически встречающихся уравнений их решение можно выполнить только приближенными методами.

Решение уравнения приближенными методами состоит из двух этапов:

1) - отделение корней, т.е. нахождение интервала изоляции для каждого корня;

2) - уточнение корней до заданной точности.

4.1.1. Для отделения корней применяют графический и аналитический способы. Часто приближенное значение корня известно из физических соображений.

Графический способ отделения корней заключается в построении графика функции f(x) или графиков более простых функций (x) и g(x), на которые может быть разбита сложная функция f(x), если ее график построить нет возможности. В первом случае точки пересечения графика f(x) с осью абсцисс, а во втором – абсциссы точек пересечения двух функций дают приближенное значение корней уравнения и позволяют оценить промежутки их изоляции.

Примеры:

а) x³ – 0,4x² – 2,37x + 0,72 = 0

Рисунок 4.1 -График функцииy = f(x)

Уравнение, как видно на графике, имеет три корня: x₁, x₂, x₃.

б) arctg x – x + 1 = 0;

arctg x = x - 1

y

Рисунок 4.2 - Графики функций y₁ = arctg (x) и y₂ = x - 1.

Уравнение имеет один корень x₁, который получен пересечением графиков двух функций: y₁ = arctg (x) и y₂ = x -1.

Аналитический метод для определения промежутков изоляции корней основан на теоремах, которые приведем без доказательств.

Т1. Если функция f(x) непрерывна на отрезке [a,b] и принимает на концах этого отрезка значения разных знаков, то внутри отрезка [a,b] существует хотя бы один корень уравнения f(x)=0.

Т2. Если функция f(x) непрерывна на отрезке [a,b] и принимает на концах этого отрезка значения разных знаков, а производная f (x) знакопостоянна внутри отрезка, то существует единственный корень уравнения f(x)=0 внутри отрезка.

Пример:

f (x) = x ³ – 0,4x ² – 2,37x + 0,72 = 0

Найдем критические точки (т.е. точки, в которых производная функции обращается в ноль):

f (x) = 3x ² – 0,8x – 2,37 = 0

x₁ = -0,765; x₂ = 1,032

Составим таблицу знаков функции (таблица 4.1):

Таблица 4.1

x	-	-2	-1	-0.76	0	1	1.032	2	+
Sign f(x)	-	-	+	+	+	-	-	+	+
Sign f (x)	+			0 (max)	-		0 (min)	+

Таким образом, как и в графическом методе, корни уравнения

x₁  (-2; -1); x₂  (0; 1); x₃  (1,032; 2).

В случае алгебраического уравнения вида

а ₀ x ⁿ + a₁ x ^n-1 + ... + a _n-1 x + a _n = 0

следует сначала определить промежутки существования всех корней, а затем применить аналитический метод.

Приведем не самый точный, но очень простой метод, который основывается на том, что все вещественные корни алгебраического уравнения с вещественными коэффициентами находятся в промежутке (-R; R), где R = 1 + A / a ₀, а A – наибольший по модулю коэффициент.

Пример: Отделить корни уравнения 8x⁴ – 32x + 1 = 0 аналитическим методом.

Решение. В этом уравнении a₀ =8, А = 32, следовательно R = 1+32/8 = 5 и корни уравнения лежат в промежутке (-5; 5). Критические точки данной функции могут быть найдены (что не всегда легко удается) из условия:

f (x) = 32x³ – 32 = 0

Здесь одна критическая точка x = 1. Построим таблицу 4.2:

Таблица 4.2 – Таблица знаков

x	-5	-4	-3	-2	-1	0	1	2	3	4	5
Sign f(x)	+	+	+	+	+	+	-	+	+	+	+
Sign f (x)	-						0	+

Анализ поведения функции показывает, что уравнение f(x) = 0 имеет два вещественных корня, которые находятся в промежутках (0; 1) и (1; 2).

Уточнение корня состоит в определении значения корня, находящегося в заданном интервале, с определенной степенью точности. Приведем несколько методов, используемых для уточнения корней.

4.1.2. Метод половинного деления основан на делении отрезка [a,b] пополам, т.е. нахождения последовательно значений X^(k), более близких к корню, по формуле:

X^{( k )} = (a+b) / 2, k = 1, 2, 3, ...

На каждом этапе отрезок [a,b] уменьшается в 2 раза и выбирается та половина, на концах которой f(x) имеет разные знаки:

если f (a)  f (x^{( k )}) > 0, то a = x^{( k )},

если f (a)  f (x^{( k )}) < 0, то b = x^{( k )}.

Этот процесс выполняется до тех пор, пока длина последнего отрезка не станет удовлетворять условию a - b < 2ε. Последнее означает, что число x = (a + b) /2 является корнем уравнения, вычисленным с точностью ε.

Пример. Найти корень уравнения 8x⁴ – 32x + 1 = 0.

на отрезке (0;1) с точностью ε=0.025 методом половинного деления.

Решение. Процесс вычисления показан в таблице 4.3.

Таблица 4.3

K	a	b	f(a)	f(b)	x(k)	f(x(k) )	b-a
1	0.00	1.0	1.00	-23.00	0.5	-14.5	1>2ε
2	0.00	0.5	1.00	-14.5	0.25	-6.9	0.5>2ε
3	0.00	0.25	1.00	-6.9	0.125	-0.3	0.25>2ε
4	0.00	0.125	1.00	-0.3	0.0625	-0.1	0.062>2ε
5	0.00	0.0625	1.00	-0.1	0.0312	-0.076	0.0312<2ε

Искомое значение корня находим по формуле:

x = (0.0625 + 0.0312) / 2 = 0.0468

Блок-схема алгоритма данного метода представлена в Приложении 6.

4.1.3. Метод хорд состоит в том, что на отрезке [a,b] строится хорда, стягивающая точки (a, f (a)) и (b, f (b)), а в качестве приближенного значения корня x_k принимается значение абсциссы точки пересечения этой хорды с осью OX.

Рисунок 4.4 - Первая и вторая производная имеют одинаковые знаки на отрезке [a;b]

Рисунок 4.5 - Первая и вторая производная имеют разные знаки на отрезке [a; b]

Эта процедура повторяется, причем отрезок сужается на каждом шаге при переносе левого или правого конца отрезка в точку пересечения хорды и оси абсцисс. (См. рис 4.4 и рис.4.5).

Расчетные формулы метода хорд имеют вид:

а) Если f  (x)  f  (x) > 0 на отрезке [a, b], то

б) Если f  (x)  f  (x) < 0 на отрезке [a, b], то

Процесс прекращается, как только x _k – x _k-1 <= ε , а последнее значение x _k считается значением корня уравнения с точностью ε. Блок-схема метода хорд представлена в Приложении 6.

4.1.4. Метод касательных заключается в вычислении последовательных приближений к корню по формуле:

п

y

ричем x₀ = a, если f  (x)  f  (x) < 0 (см. рис.4.7) и x₀ = b, если f (x)  f (x) > 0 (см. рисунок 4.6) на заданном отрезке. За приближенное значение к корню принимается абсцисса точки пересечения касательной, проведенной к одной из точек дуги AB, с осью OX. Процесс вычислений прекращается при выполнении условия x _k – x _k-1  ε.

Рисунок 4.6. - Функция f(x) возрастает на отрезке [a; b].

Рисунок 4.7 - Функция f(x) убывает на отрезке [a; b]

Блок-схема алгоритма метода касательных представлена в Приложении 6.

4.1.5. Комбинированный метод состоит в объединении двух последних описанных методов. Целесообразность его состоит в том, что для непрерывных функций f (x) с непрерывными производными, не меняющими знака на отрезке [a, b], приближение к корню осуществляется с разных сторон. Графически этот метод изображен на рис. 4.8.

x

Рисунок 4.8 - Случай возрастающей выпуклой вниз функции

Вычислительная процедура подчиняется правилу:

а) Если f  (x)  f  (x) > 0 на отрезке [a, b], то

б) Если f  (x)  f  (x) < 0 на отрезке [a, b], то

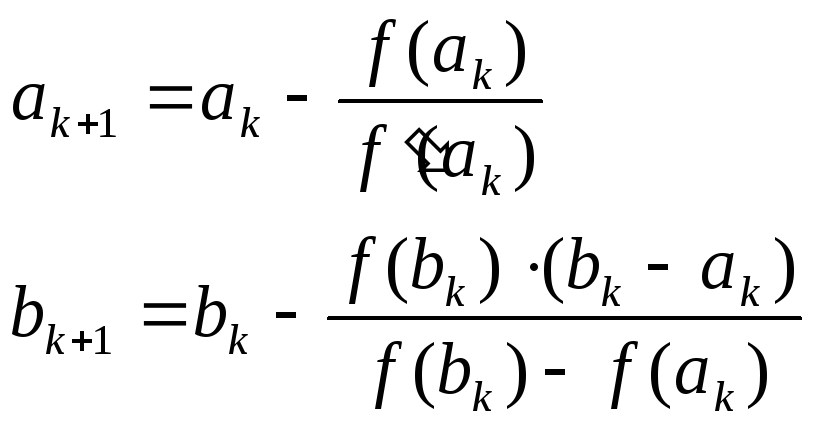
Вычисления прекращаются при выполнении условия b _k+1 – a _k+1 2ε и в качестве значения корня, полученного с точностью ε, принимается

x = (a _k+1+ b _k+1) /2.

Пример: Найти корень уравнения 8x⁴ – 32x + 1 = 0 на отрезке [1,2] с точностью 0,01, используя комбинированный метод.

Решение. Корень уравнения отделен и находится на отрезке [1,2]. На левом конце отрезка производная данной функции равна нулю. Для выполнения расчетов следует сузить отрезок таким образом, чтобы в отрезке и на его концах производные функции были знакопостоянны и не равны нулю. Возьмем отрезок [1,1; 2]. На концах отрезка функция принимает значения разных знаков, первая производная f  (x) >0 и f  (x) > 0. Это означает, что уравнение имеет один корень на отрезке [1,1; 2] и можно воспользоваться формулами (а) комбинированного метода.

Разность b₁ - a₁ = 0,38, что превышает заданную точность ε = 0,01. Продолжая вычисления по формулам (а), получим:

a ₂ = 1,53; b₂ =1,59

a ₃ = 1,576; b₃ =1,577.

Последние значения имеют разность меньше 2ε = 0,02, и значение корня может быть принято

x = (1,576 + 1,577) / 2 = 1,5765

Блок-схема алгоритма комбинированного метода представлена в Приложении 6.

4.1.4. Метод итераций заключается в том, что исходное уравнение вида f(x) = 0 заменяется равносильным уравнением вида x = (x), таким образом, чтобы функция (x) удовлетворяла условию (x) < 1 на отрезке [a,b]. Эта замена может быть выполнена по формуле:

 (x) = x – f (x) / k,

где k выбрано так, чтобы k > Q / 2, где Q = maxf (x) и знак k совпадал бы со знаком f (x) на отрезке [a, b]. Тогда метод последовательного приближения к корню заключается в том, что после выбора любого начального приближения к корню x₀ [a, b] первое приближение к корню x₁ вычисляется путем подстановки x₀ в правую часть преобразованного уравнения, т.е. x₁ = (x₀). Для вычислений второго и всех последующих приближений используется расчетная формула:

x _k+1 =  ( x _k).

Таким образом строится последовательность приближений x₀, x₁,... x _k и процесс вычислений прекращается при выполнении условия x _k+1 – x _k <= ε. Последнее значение, полученное в результате вычислений, можно принять за корень уравнения f (x) = 0, полученный с заданной степенью точности ε.

Блок-схема алгоритма метода итераций представлена в Приложении 6.