4.2 Приближенное вычисление определенных интегралов

Численное интегрирование основано на геометрическом смысле определенного интеграла, который заключается в том, что значение

равно площади фигуры, ограниченной осью абсцисс, прямыми x = a, x = b и кривой подынтегральной функции. Эту фигуру (криволинейную трапецию) разбивают на ряд элементарных фигур с легко вычисляемыми площадями, суммирование которых дает искомое значение интеграла.

4.2.1. Формула прямоугольников. Разбиение интервала интегрирования [a ,b] на n частей приводит к возможности рассмотрения площадей криволинейных трапеций на каждом небольшом отрезке [x_i; x_i+1]. Учитывая малую величину шага разбиения h = (b-a)/n, площадь такой фигуры можно считать приближенно равной площади прямоугольника со сторонами y_i и h (см. рисунок 4.9).

Рисунок 4.9 - Графическая интерпретация метода прямоугольников

Суммирование значений таких площадей (S_i = y_i  h) позволяет получить формулу

«левых» прямоугольников

Блок-схема этого метода представлена в Приложении 6.

4.2.2. Формула трапеций. Замена интеграла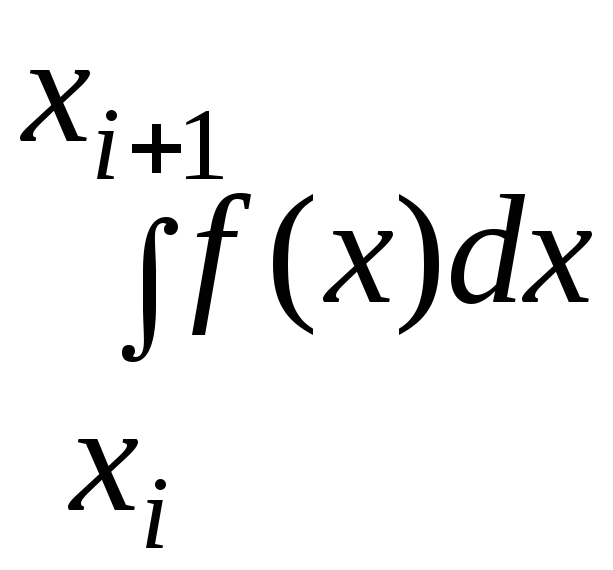на каждом элементарном участке площадью трапеции с основаниями y_i =f (x _i), y _i+1 =f (x _i+1) и высотой h (S _i = h(y _i + y _i+1) / 2) приводит после суммирования к следующей формуле:

Блок-схема метода трапеций представлена в Приложении 6.

4.2.3. Формула Симпсона. Разбиение промежутка [a, b] на четное число (n=2m) отрезков позволяет на каждой паре отрезков [x _i; x _i+2] заменить подынтегральную функцию параболой y(x) = A_i x² + B_i x + C_i. Площадь фигуры, ограниченной сверху параболой, считается по формуле:

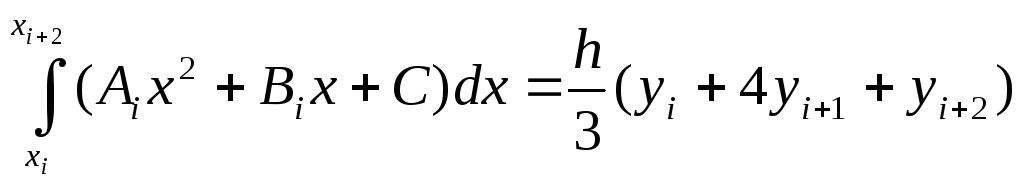
Суммирование таких интегралов (площадей, ограниченных параболами) приводит к более точной, чем предыдущие, формуле:

Пример. Вычислить

а) Формула Ньютона-Лейбница

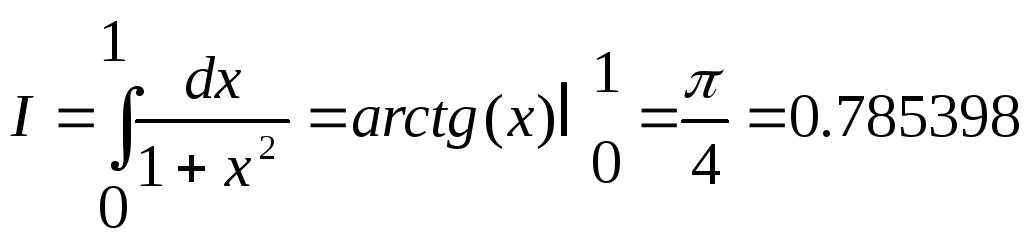
б) Разобьем отрезок [0, 1] на 4 части. Шаг разбиения h = 0,25. Вычисляем в каждой точке разбиения значение подынтегральной функции .

I	0	1	2	3	4
X	0	0.25	0.5	0.75	1
Y	1	0.941	0.8	0.64	0.5

Формула трапеций

I =h  ((y₀ + y₄) / 2+ y₁ + y₂ + y₃) = 0.25  ((1 + 0,5) / 2 + 0.941 + 0.8 + 0.64) =0,7828

Формула Симпсона:

I = (h / 3)[y₀ + 4(y₁ + y₃) + 2y₂ + y₄] = (0,25 / 3) [1 + 4(0,9412 + 0,64) + 20,8 + 0,5] = 0,7854

Расчеты показывают хорошее совпадение результатов, полученных численным интегрированием, с результатом непосредственного интегрирования. Увеличение числа разбиений приведет к более точным результатам.

При вычислении интегралов описанными методами оценить количество разбиений отрезка удается достаточно редко. В таком случае следует выполнить расчеты интеграла для шага h и h / 2, и полученные значения сравнить. Если для формулы Симпсона оценочная величина больше заданной точности ε, то приходится уменьшать шаг до h / 4 и т.д., пока на каком-то этапе не будет выполнено условие:

Данный алгоритм позволяет вычислить значение интеграла с автоматическим выбором шага. Его схема представлена в Приложении 6, где для удобства программирования использована измененная формула Симпсона:

3. Решение систем линейных уравнений

Методы решения систем линейных уравнений можно разделить на три группы: точные (Крамера, Гаусса, и др.), итерационные и специальные (прогонки). В этом разделе изложены итерационные методы, т.к. точные методы очень полно излагаются в курсе высшей математики, а специальные применяются для систем специфического характера.

Рассмотрим систему из n уравнений:

Разрешив первое уравнение относительно x₁, второе – относительно x₂ и т.д., получим:

Правые части уравнений последней системы можно рассматривать как функции от неизвестных x₁, x₂, ... x_n, и тогда систему можно представить в виде:

4.3.1. Метод итераций. Если задать начальные приближения x₁⁽⁰⁾, x₂⁽⁰⁾, ... x_n⁽⁰⁾, следующие приближения к неизвестным будут получены подстановкой начальных приближений в правую часть преобразованной системы. Найденные значения можно использовать снова (процесс итераций), т.е.

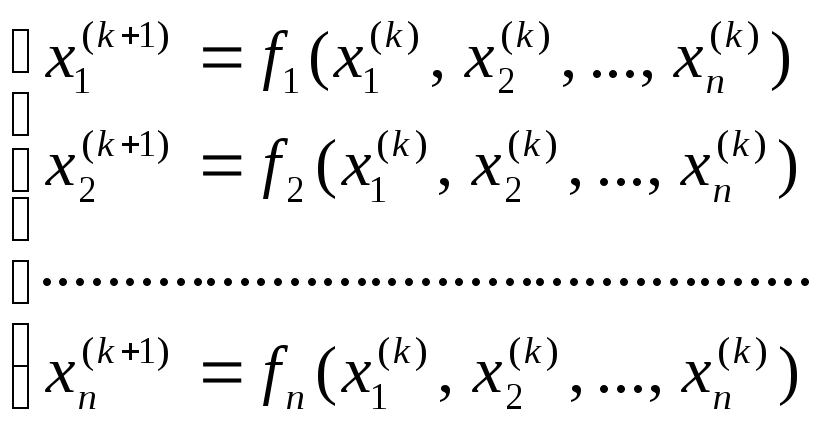
где x _i^(k) – приближения, полученные на k-м шаге итерации.

Процесс продолжается до тех пор, пока значения  x_i^(k+1) - x_i^(k) не станут меньше заданной точности ε для всех i = 1,2,... n. Последние полученные приближения являются решением системы уравнений с точностью ε.

Для применения метода итераций существенным является требование сходимости последовательности приближений к решению системы. Итерационный процесс сходится, если сумма отношений модулей коэффициентов каждой строки к диагональному будет строго меньше единицы:

Неравенство будет справедливо, если диагональные элементы системы удовлетворяют условию:

Выбор начальных приближений не влияет на условие сходимости, поэтому можно полагать их равными нулю: (x_i⁽⁰⁾ = 0, i=1,2,.. n) или отношениям свободных коэффициентов к диагональным: (x_i⁽⁰⁾ = b_i /a_i,i, i=1,2,.. n).

Пример. Решить систему уравнений методом итераций с точностью  = 0,005.

x₁ + 4x₂ – x₃ = 4

5x₁ – x₂ + 10x₃ = 14

7x₁ – 5x₂ + 2x₃ = 4

В системе первое уравнение имеет преобладающий коэффициент при неизвестном x₂, а второе – при x₃, а в третьем уравнении такого нет. Сложив первое и третье уравнение системы, можно получить преобладающий элемент при x₁. Переставив уравнения так, чтобы по диагонали стояли преобладающие элементы, получим:

Условия сходимости для коэффициентов преобразованной системы выполняются, т.к. 8 >  (1+1); 4 >  (1+1); 10 >  (5+1).

Разрешив уравнения относительно неизвестных, запишем:

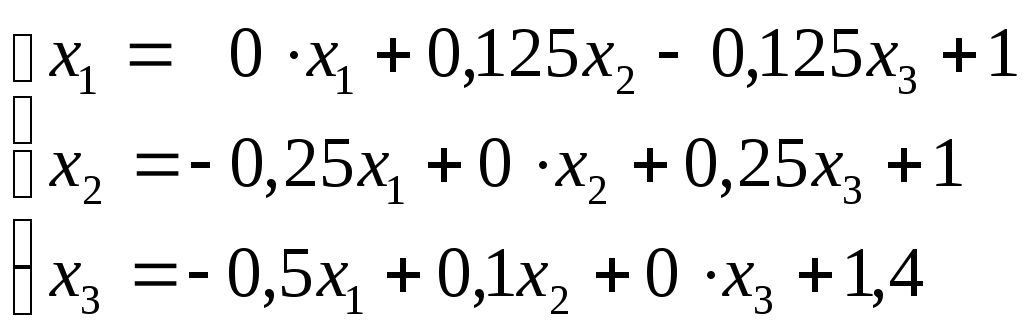
Выберем начальные приближения x₁⁽⁰⁾ = 1, x₂⁽⁰⁾ = 1, x₃⁽⁰⁾ = 1,4. Тогда

Дальнейшие итерации дадут значения приближений: x⁽²⁾ = (1,0125; 1,0125; 1,035); x⁽³⁾ = (1; 1,005; 0,995); x⁽⁴⁾ = (1,000; 1,001; 1,000). Последнее приближение можно считать решением системы с точностью ε =0.005, т.к. max  x_i⁽⁴⁾ – x_i⁽³⁾ = 0,005. Блок-схема алгоритма метода итераций представлена в Приложении 6.

4.3.2. Метод Зейделя. Рассмотренный итерационный процесс можно модифицировать. Для вычисления приближения x_i^(k+1) были использованы, полученные на предыдущем шаге x_i^(k), i=1,2, ..., n. Но к этому моменту уже найдены значения x₁^(k+1), x₂^(k+1), ... x_i-1^(k+1), поэтому для определения x_i^(k+1) имеет смысл их применить, т.е.

Для составления блок-схемы алгоритма метода Зейделя воспользуемся формулой получения приближения на (k+1)-м шаге в виде:

где i = 1, 2, ..., n. На каждом шаге итерации будем вычислять погрешности R_i^(k) = x_i^(k+1) – x_i^(k) и сравнивать их с заданной точностью ε. Блок-схема алгоритма метода Зейделя представлена в Приложении 6.