2.3. Характерные приемы алгоритмизации

2.3.1 Вычисление конечных сумм и произведений

Вычисление конечной суммы сводится к нахождению суммы некоторого количества слагаемых

S =,

где i – номер слагаемого, f_i – слагаемое с номером i.

Вычисление суммы организуется в виде циклического процесса, когда при каждом прохождении цикла номер слагаемого изменяется на 1, а сумма изменяется на величину i-го слагаемого. Процесс выполняется до тех пор, пока не будут просуммированы все n слагаемых.

Пример 7: Вычислить сумму S =.

Формула суммирования записывается следующим образом: S = S + f ( i ).

Это означает, что к предыдущему значению суммы добавляется значение i-го слагаемого, и вычисленное значение присваивается той же переменной S. Если начальное значение S приравнять к нулю, то после первого выполнения цикла значение S будет равно значению первого слагаемого: S = 0+f (1). После второго шага значение S будет равно сумме двух первых слагаемых: S = S + f (2) = = f (1) + f (2) и т.д. Блок-схема алгоритма приведена на Рисунке 2.5.

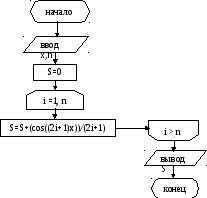
Рисунок 2.5 - Блок-схема алгоритма к задаче №7.

Блок присваивания начального значения сумме S = 0 должен быть расположен до начала цикла, в котором накапливается эта сумма (границы цикла – это блоки 4-й и 6-й). Поскольку результат решения - одно число (значение суммы), то оператор печати стоит за циклом и выполняется один раз. В случае необходимости получения промежуточных значений суммы оператор печати S можно поместить внутри цикла накапливания этой суммы.

Вычисление конечного произведения представляет собой нахождение произведения заданного количества сомножителей

где i - номер сомножителя; f_i - сомножитель с номером i.

Начальное значение произведения должно быть равно единице. Формула накапливания произведения значений функции аналогична формуле суммирования и имеет вид: P = P  f ( i ) .

Пример 8: Вычислить произведение положительных элементов массива

X={x₁, x₂, ... x₁₀}.

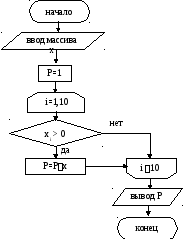
Рисунок 2.6 - Схема алгоритма вычисления произведения.

Блок 3 задает начальное значение произведения равное единице. Перед вычислением произведения проверяется, является ли сомножитель положительным (блок 5). В блоке 6 вычисляется новое значение произведения. При невыполнении условия x_i > 0 осуществляется переход к следующему значению переменной цикла.

2.3.2. Понятие массивов и их обработка. Для представления в программе векторов, матриц и подобных им объектов используются массивы. Массивом называется упорядоченная последовательность величин, обозначенных одним именем. В отличие от переменной, которая занимает одну ячейку памяти ЭВМ, под массив отводится столько ячеек, сколько элементов в нем содержится.

Отдельные величины, образующие массив, называются элементами массива. К каждому элементу массива можно обратится, указав имя массива и индексы, которые указывают положение элемента в массиве. Таким образом, переменная с индексами является элементом массива. Количество индексов, используемых для обозначения массива, зависит от pазмерности массива, т.е. от количества его измеpений.

Если число измерений равно единице, то массив называется одномерным. Одномерные массивы отображают в программе векторы или линейные таблицы. Переменная с одним индексом - элемент одномерного массива. Значение индекса определяет порядковый номер элемента в массиве, например, А(3) - это третий элемент массива А.

Массив с двумя измерениями называется двумерным массивом и описывает в программе матрицу или прямоугольную таблицу. Переменная с двумя индексами - элемент двумерного массива (матрица). Значение первого индекса определяет номер строки, а значение второго - номер столбца прямоугольной таблицы, на пересечении которых находится данный элемент. Например, В(2,5) - это элемент второй строки и пятого столбца матрицы В.

Представление данных в виде таблицы оказывается целесообразным, а в некоторых случаях и единственно возможными при решении многих практических задач: действия с векторами и матрицами, вычисление таблицы значений функции в произвольных точках, сортировка массивов, отыскание наибольших и наименьших значений в наборах данных и т.д.

Пример 9: Вычислить и запомнить значения функции ,

где x(i) - элементы массива Х, состоящего из 20-ти чисел.

При решении данной задачи для хранения значений функции Y резервируется массив. Текущее значение функции Y обозначают переменной с индексом – y(i) так же, как и текущее значение аргумента x_i.

Рисунок 2.7.- Схема алгоритма к задаче №9.

В блоке ввода исходных данных предусматривается ввод значений элементов массива Х и переменных a и b. Параметром цикла является не само значение аргумента, а номер i очередного значения аргумента в массиве Х. Вычисленное значение функции y_i также является переменной с индексом, т.е. каждое значение функции запоминается в массиве Y. Вывод результатов (значений y_i) можно осуществлять как внутри цикла, в котором происходит вычисление y_i, так и в отдельном цикле.

Пример 10: Определить количество положительных элементов массива А={a₁,......,a₄₀} и вычислить их сумму.

Блок-схема алгоритма приведена на рисунке 2.8. Вычисление количества и суммы положительных элементов массива ведется одновременно в цикле, параметром которого служит номер элемента в массиве. Формула накапливания суммы в данном случае имеет вид s = s + a_i, а формула накапливания количества – k = k+1, причем вычисления по этим формулам выполняются только для положительных элементов массива (проверка условия для выбора положительных элементов - блок 6). Перед началом цикла переменным s и k присваиваются начальные нулевые значения. (Блоки 3 и 4).

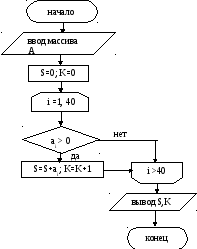
Рисунок 2.8. - Схема алгоритма к задаче №10.

Пример 11. Найти элемент массива X = (x₁, x₂, ... x_n) с наименьшим значением и его порядковый номер.

Алгоритм поиска наименьшего значения массива заключается в просматривании по порядку всех элементов массива и сравнении значения текущего элемента с наименьшим из значений всех предыдущих элементов. Если значение текущего элемента окажется меньше наименьшего из предыдущих, то его следует считать новым наименьшим значением. В противном случае наименьшее значение остается прежним.

Данный алгоритм описывается следующим образом:

.

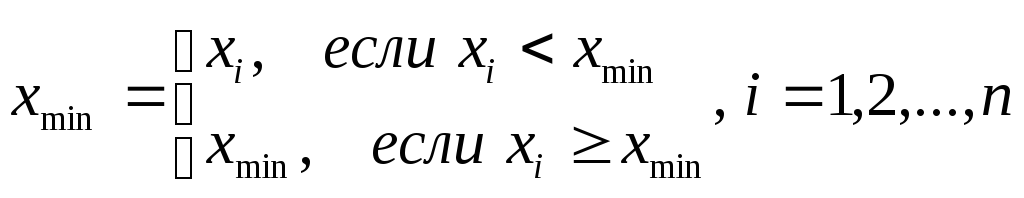Перед началом цикла переменной X_min присваивается начальное значение, представляющее собой значение элемента x₁ (см. Рисунок 2.9) Циклический просмотр элементов массива в этом случае начинается со второго элемента для исключения сравнивания x₁ с самим собой.

Для запоминания номера наименьшего элемента введена переменная N_min, начальное значение которой равно номеру первого элемента, т.е. единице. Как только очередной элемент x_i массива оказывается меньше Xmin, номер i этого элемента запоминается в переменной N_min. Если при выполнении алгоритма окажется, что условие x_i<X_min не выполнилось ни разу, то значения переменных X_min и N_min останутся равными начальным значениям x₁ и 1. Это означает, что ни один элемент в массиве не оказался меньше первого, т.е. наименьший элемент – с номером 1.

Аналогично решается задача нахождения наибольшего значения среди элементов массива:

.

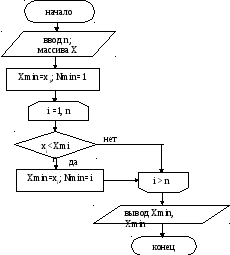
Рисунок 2.9 - Схема алгоритма выбора наименьшего значения в массиве.

В случае поиска наименьшего (наибольшего) значения среди вычисляемых элементов выбор начального значения или переменной, обозначающей это наименьшее (наибольшее) значение, осуществляется следующим образом:

если выбирается минимальное значение, то переменной min присваивается значение заведомо большее, чем любое из ожидаемых значений элементов (например: min = 10⁵);

если выбирается максимальное значение, то переменной max присваивается значение заведомо меньшее, чем любое из ожидаемых значений элементов (например: max = -10⁵).

Пример 12. Определить максимальное значение функции Y = cos(x_i) - lnx_i для заданного массива X = (x₁,x₂,... x₁₇).

Максимальное число обозначим max, которому первоначально присвоим заведомо малое число, например, -10⁸, чтобы, сравнивая его с первым значением Y, получить в качестве максимума первое значение функции Y.

Итак, после вычисления Y₁ получим max₁ = max(max₀,Y₁) = Y₁, поскольку в качестве предыдущего максимума взяли число, которое заведомо было меньше любого значения функции Y. Далее определим max₂: max₂ = max(max₁,Y₂); max₃ = max(max₂,Y₃),... max_n = max(max_n-1, Y_n). Повторяя этот разветвленный процесс n раз, получим значение max, равное наибольшему значению функции Y (см. Рисунок 2.10 ).

Рисунок 2.10 - Схема алгоритма выбора наибольшего значения функции.

2.3.3. Алгоритмы со структурой вложенных циклов. Любой цикл может содержать внутри себя один или несколько других циклов. Такая структура называется вложенными циклами. Охватывающие циклы называются внешними, охватываемые – внутренними. Вложенные циклы используются, например, для обработки матриц.

Параметры внешнего и внутреннего циклов должны быть разными. Они изменяются не одновременно, т.е. при одном значении параметра внешнего цикла параметр внутреннего цикла принимает поочередно все свои значения.

Приемы программирования, изложенные ранее, можно использовать и при организации вложенных циклов, т.е. при обработке матриц.

Пример 13. Вычислить произведение элементов заданной матрицы A(5,5), значения которых лежат в диапазоне 1  a_ij  10 (i, j = 1,2,...5).

Чтобы найти произведение всех элементов матрицы, удовлетворяющих заданному условию, перебираются все элементы матрицы от a₁₁ до a₅₅. Для каждого элемента a_ij проверяется заданное условие и, в случае его выполнения, вычисляется очередное значение произведения по формуле P = Pa_ij. Элементы просматриваются с помощью вложенных циклов, причем порядок вложения циклов значения не имеет. Более удобным является традиционный порядок работы с матрицами – по строкам. В этом случае внешним является цикл по номеру строки i, а внутренним – цикл по номеру элемента столбца j (см. Рисунок 2.11). Переменной P до начала цикла присваивается начальное значение, равное единице.

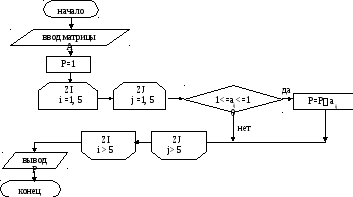
Рисунок 2.11 - Блок-схема алгоритма к задаче №13.

Пример 14. Вычислить сумму положительных элементов каждой строки матрицы A(6,5).

Для вычисления суммы положительных элементов одной строки матрицы организуется цикл, перебирающий все элементы строки, параметром цикла является номер столбца j. Перед циклом задается начальное значение суммы S=0. После окончания цикла результат выводится на печать. Если все эти действия повторяются во внешнем цикле изменения индекса строки i, то будут вычислены все ШЕСТЬ сумм.

В рассмотренном примере внешний цикл обязательно должен быть по i (индексу строки), т.к. в противном случае были бы вычислены суммы положительных элементов каждого столбца.

Рисунок 2.12 - Блок-схема алгоритма к задаче №14.