
21
ния.
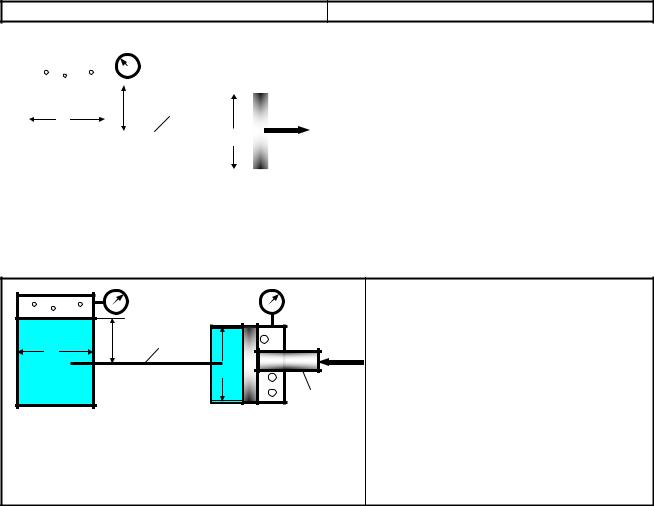
Задача 23
|
|
|
|
|
рv |
|
|
|
Дано: диаметр цилиндров D и d0, длина |
|||
|
|
|
|
|
|
|
|
|
|
|
l и диаметр трубопровода d, плотность |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
жидкости ρ, динамический коэффици- |
|
|
|
|
|
H |
|
|
|
|
|
|||
|
d0 |
|
|
|
|
|
|
|
ент вязкости η, расход Q, сила R, по- |
|||
|
|
|
|
l, d |
|
|
|
R |
||||
|
|
|
|
|
|
|
казание вакуумметра pv, высота H, эк- |
|||||
|
|
|
|
|
D |
|
||||||
|
|
|
|
|
|
|
|
|
вивалентная шероховатость трубопро- |
|||
|
|
|
|
|
|
|
|
|
|
|
вода |
э. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Определите по этим данным экспери- |
|
|
|
|
|
|
|
|
|
|
|
|
ментальное и теоретическое значение |
|
|
|
|
|
|
|
|
|
|
|
|
коэффициента гидравлического тре- |
|
|
|
|
|
|
|
|
|
|
|
|
ния. |
|
Задача 24 |
рм1 |
рм2 |
Дано: диаметр цилиндров D и |
||
|
|||||
|
|
|
d0>>D, длина l и диаметр трубо- |
||
H |
|
|
провода d, плотность жидкости |
||
|
|
ρ, динамический коэффициент |
|||
d0 |
l, d |
R |
|||
вязкости η, расход Q, сила R, по- |
|||||
|
|
D |
казание манометров pм1 и рм2, вы- |
||
|
|
dшт |
сота H, эквивалентная шерохова- |
||
|
|
|
тость трубопровода |
э. |
|
диаметр штока dшт<<D и им можно |
Определите по этим данным экс- |
||||
периментальное и теоретическое |
|||||
пренебречь |
|
|
|||
|
|
значение коэффициента гидравли- |
|||
|
|
|
ческого трения. |
|
|
22
ПРИЛОЖЕНИЯ
Приложение 1 Значение эквивалентной шероховатости для различных труб.
Вид трубы |
Состояние трубы |
э, мм |
Бесшовная стальная |
новая |
0,02÷0,05 |
|
после нескольких лет |
|
|
эксплуатации |
0,15÷0,3 |
Стальная сварная |
новая |
0,03÷0,1 |
|
умеренно заржавленная |
0,3÷0,7 |
|
сильно заржавленная |
2,0÷4,0 |
Чугунная |
новая |
0,2÷0,5 |
|
бывшая в употреблении |
0,5÷1,5 |
|
|
|
|
|
|
|
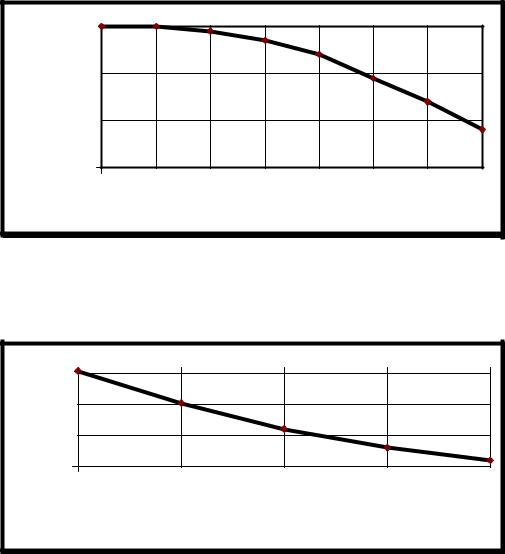
Приложение 2 |
Зависимость плотности воды от температуры |
|||||||
м. |
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
/кубкг999 |
|
|
|
|
|
|
|
998 |
|
|
|
|
|
|
|
плотность, |
|
|
|
|
|
|
|
997 |
|
|
|
|
|
|
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
|
температура, град. Цельсия |
|
|
|||
|
|
|
|
|
|
|
Приложение 3 |
Зависимость кинематического коэффициента вязкости воды |
|||||||
|
ν, 10-6 м2/с температуры |
|
|
||||
1,25 |
|
|
|
|
1 |
|
|
|
|
0,75 |
|
|
|
|
0,5 |
|
|
|
|
10 |
20 |
30 |
40 |
50 |
|
температура. град. Цельсия |
|
||
23
Приложение 4 Определение теоретического значения коэффициента трения
для вязкопластичной жидкости
Неньютоновские жидкости - это жидкости со сложной внутренней структурой, которая перестраивается при изменении скорости движения, что приводит к изменению вязкости жидкости.
Внефтегазовом деле широко применяется модель вязкопластичной жидкости с параметрами: ρ - плотность, η - пластическая вязкость (вязкость в началь-
ный момент движения, при нулевой скорости), и τ0 - начальное напряжение сдвига.
Вэтом случае коэффициент трения есть функция двух безразмерных пара-
метров:
λ = f(Re*, э/d).
Число Re*( Число Рейнольдса со звездочкой) определяется так:
Re*=ϑ d ρ/ηэ,
где ηэ - переменная (зависящая от скорости движения) вязкость такой жидкости.
ηэ = η(1 + 16 Bi )
ηэ = η(1 + 18 Bi )
Bi = τ o dг
η ϑ
Здесь первая формула используется для круглого сечения канала, вторая - для кольцевого.
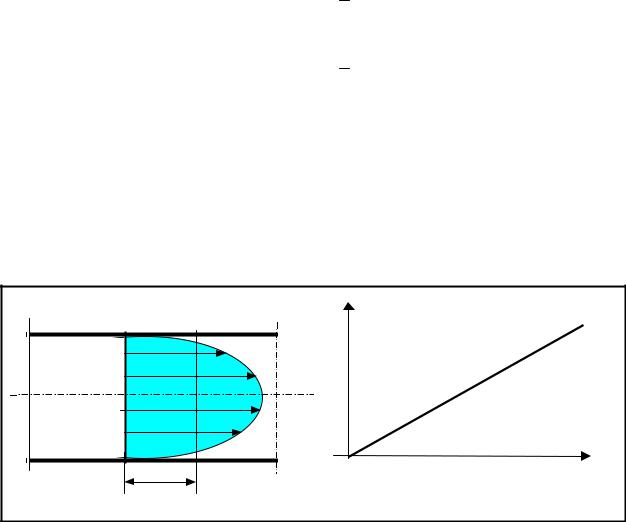
На практике при движении вязкопластичной жидкости не осуществляется стандартный ламинарный режим движения, при котором имеет место параболическое изменение скорости от нуля на стенке до максимума на оси и потери напора (давления) пропорциональны первой степени скорости (рис. 1).
«а» |
hдл ( рдл) |
«в» |
ϑ |
0 |
ϑ |
|
|
|
“а”- параболическая эпюра местных скоростей; |
|
|
“в”- зависимость потерь напора (давления) от скорости движения. |
||
24
Рис.1. К ламинарному режиму движения ньютоновской жидкости.
Докажем, что при ламинарном режиме потери давления пропорциональны первой степени скорости движения.
p = ρ λ |
l |
ϑ2 |
= ρ |
64 l ϑ2 |
= ρ |
64 η l ϑ2 |
= k ϑ; |
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
Re d 2 |
ϑ d ρ d 2 |
||||||||||||
|
|
d 2 |
|
|
|
|||||||||
k = |
64 η l |
= const − угловой коэффициент прямой. |
||||||||||||
2d 2 |
|
|||||||||||||
Определим зависимость потерь давления от скорости при движении вязкопластичной жидкости.
p = ρ λ |
l ϑ2 |
|
|
|
|
|
64 l ϑ2 |
|
|
64 ηэ l ϑ2 |
|
|||||||||||||||||||||||
|
|
|
2 = ρ |
|
|
|
|
|
|
|
|
2 = ρ |
|
|
|
2 = |
||||||||||||||||||
d |
Re* |
d |
ϑ d ρ |
d |
||||||||||||||||||||||||||||||
64 |
η(1 + |
|
|
τ0 d |
|
|
) |
|
l |
|
υ2 |
|
64 l ϑ2 |
|
16τ |
|
l |
|
||||||||||||||||
η ϑ 6 |
|
|
|
0 |
; |
|||||||||||||||||||||||||||||
ρ |
|
|
|
|
|
|
|
|
|
= ρ |
+ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ϑ d |
ρ |
|
|
|
|
|
|
d 2 |
Re d 2 |
|
3d |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
p = ρ |
64 |
|
|
l |
ϑ2 |
+ |
16τ |
0 |
l |
|
|
(1) |
|
|
|
|
|
|
|
|
||||||||||||||
Re d |
2 |
|
|
|
|
3d |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
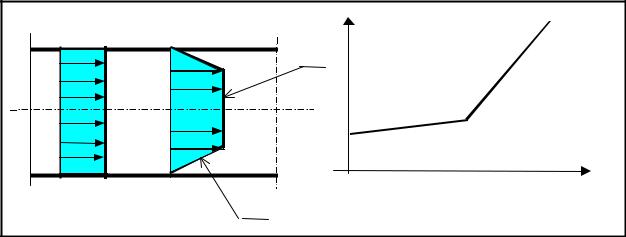
Как следует из уравнения (1), для начала движения вязкопластичной жидкости (ϑ=0) необходимо создать перепад давления, соответствующий равенству возникающего в жидкости касательного напряжения τ ее начальному напряжению сдвига τо. При этом вся масса жидкости отрывается от стенок трубы и движется первоначально как одно целое с одинаковыми для всех частиц скоростями (рис. 2”a”).
«а» |
«б» |
|
hдл ( рдл) |
«в» |
|
|
2 |
|
|
|
|
0 |
|
ϑ |
|
|
1 |
|
|
|
1- градиентный слой, 2 |
- ядро потока. |
|
|
Рис.2. Особенности структурного режима движения вязкопластичной жидкости. |
||||
При дальнейшем увеличении скорости наблюдается так называемый структурный режим движения, при котором имеется центральное ядро, где жидкость движется как твердое тело с постоянной скоростью, и градиентный слой, где скорость уменьшается до нуля на стенке трубопровода (рис.2”б”).
25
При критическом значении числа Re* структурный режим переходит в турбулентный.
Уравнение (1) можно переписать в виде:
p = c(η ϑ + |
τ o d ) |
, |
(2) |
|
6 |
|
|
где с=32 l/d2.
Из уравнения (2) следует, что при малых скоростях движения, когда τ0 d/ 6 >> η ϑ потери давления практически не зависят от скорости (рис.2”в”).
Для вязкопластичной жидкости коэффициент трения при структурном режиме определяется так:
λ |
= |
6 4 |
-при движении в круглой трубе |
(3) |
|
R e |
|||||
|
|
||||
λ |
= |
9 6 |
-при движении в кольцевом канале |
(4) |
|
R e |
|||||
|
|
|
|
R e |
|
= |
ϑ d г |
ρ |
-критерий Рейнольдса |
||
|
η э |
|
|||||
η э |
= |
|
|
6 B i ) |
-эффективная вязкость при движении |
||
|
η ( 1 + 1 |
/ |
|||||
|
|
|
|
|
|
|
в круглой трубе |
η э |
= |
|
η ( 1 + 1 |
/ |
8 B i ) |
-эффективная вязкость при движении |
|
|
|
|
|
|
|
|
в кольцевом канале |
|
|
B i = |
τ o |
d г |
|
-критерий Бингама |
|
|
|
|
|
η ϑ |
|
|
|
Здесь dг - гидравлический диаметр, равен диаметру трубопровода при движении жидкости в трубе и (D-d) при движении в кольцевом канале.
При турбулентном режиме рекомендуются следующие формулы:
Re = 2000÷40000 |
λ = 0,08(Re )-1/7 - формула Миттельмана |
(5) |
|||||||
Re |
|
>40000 |
λ = 011, ( |
68 |
+ |
э |
) |
0 ,25 |
(6) |
|
Re |
d |
|
||||||
Критическое число Рейнольдса, определяющее переход к турбулентному режиму, равно 2100 для круглой трубы и 1000 для кольцевого канала.
