0,7 Мкм) при таких температурах имеет слишком малую энергию и не может быть обнаружено невооруженным глазом.

      Так как в сторону неба система наземных тел не является замкнутой, то равновесия между телами у поверхности Земли и их излучением не устанавливается. Поэтому все тела, температура которых несколько больше, чем температура земной поверхности, могут быть зафиксированы в микроволновом диапазоне как излучающие объекты. Увидеть такие источники инфракрасного излучения можно только с помощью специальных приборов, в которых микроволновое невидимое глазом излучение регистрируется специальными датчиками инфракрасного излучения и преобразуется в модулированные электрические сигналы, которые управляют электронным пучком, дающим на экране кинескопа видимое изображение предметов.

      В конце XX в. произошло качественное изменение техники ночного видения, связанное с созданием электронно-оптических преобразователей нового типа. С помощью современных биноклей и прицелов ночного видения наблюдатель может получить в темноте видимое изображение достаточно высокого качества человека на расстоянии нескольких сот метров или движущегося танка на расстоянии нескольких километров. А пилотажные очки ночного видения позволяют эксплуатировать вертолеты в условиях ограниченной видимости практически круглые сутки.

     

     Задача 1.1. Покажите, что если излучение происходит в объеме достаточно толстого слоя из любого вещества, имеющего на единицу толщины испускательную способность и поглощательную способность , то поверхность этого слоя излучает как абсолютно черное тело. При расчетах ограничиться рассмотрением излучения, распространяющегося в направлении, перпендикулярном поверхности слоя.

      Решение: Пусть слой вещества, занимающего полупространство , имеет температуру (рис. 1.6). Выделим тонкий слой этого вещества с координатами от до . На частоте этот тонкий слой излучает по направлению к поверхности поток энергии с единицы площади .

Рис. 1.6.

      До выхода с поверхности слоя это излучение проходит слой поглощающего вещества толщиной . При этом по закону Бугера поток энергии излучения уменьшается экспоненциально и при выходе на поверхность становится равным

     

.

     Суммируя излучение от всех слоев, находим испускательную способность поверхности слоя

     

.

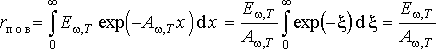      Но по закону Кирхгофа 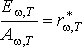, где - испускательная способность абсолютно черного тела. Поэтому , и мы тем самым доказали, что поверхность слоя излучает как абсолютно черное тело.

      Этот важный вывод поясняет, например, почему излучение с поверхности достаточно большого объема высокотемпературной плазмы и, в частности, с поверхности Солнца, близко по спектральному составу к излучению абсолютно черного тела.

      Задача 1.2. Максимум испускательной способности Солнца приходится на длину волны мкм. Считая излучение Солнца близким к излучению абсолютно черного тела, оцените суммарную площадь панелей солнечной батареи мощностью кВт на орбитальной околоземной космической станции. К.п.д. солнечной батареи принять равным . Астрономические величины взять из таблиц.

      Решение: Из закона смещения Вина по формуле (1.11) определим температуру поверхности Солнца

     

.

      Теперь по закону Стефана-Больцмана находим энергетическую светимость Солнца и полную мощность излучения с его поверхности

     

.

     Здесь м - радиус Солнца.

      Считая, что Солнце излучает по всем направлениям изотропно, находим солнечную постоянную , равную потоку энергии излучения через единицу поверхности сферы, радиус которой равен среднему расстоянию от Солнца до Земли м. При этом

     

.

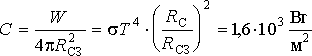      Итак, в космическом пространстве вблизи Земли на каждый квадратный метр поверхности, перпендикулярной солнечным лучам, за одну секунду падает 1,6 кДж энергии солнечного излучения. Часть этой энергии в солнечной батарее превращается в электрическую энергию. С учетом к.п.д. солнечной батареи, находим ее электрическую мощность

     

.

     Отсюда определяем площадь панелей солнечной батареи

     

.

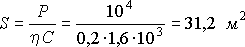     1) Звездочкой в дальнейшем мы будем отмечать характеристики теплового излучения абсолютно черного тела.

66

Фотоэффе́кт, Фотоэлектрический эффект — испускание электроноввеществом под действием света (или любого другого электромагнитного излучения). В конденсированных (твёрдых и жидких) веществах выделяют внешний и внутренний фотоэффект.

Законы Столетова для фотоэффекта:

Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока.

Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.

3-й закон фотоэффекта: для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света (или максимальная длина волны λ₀), при которой ещё возможен фотоэффект, и если , то фотоэффект уже не происходит.

Теоретическое объяснение этих законов было дано в 1905 году Эйнштейном. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. Поглотив фотон, электрон получает от него энергию и, совершая работу выхода φ, покидает металл: где — максимальная кинетическая энергия, которую имеет электрон при вылете из металла.

67

Фото́н — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать в вакууме только двигаясь со скоростью света. Электрический заряд фотона также равен нулю. Фотон может находиться только в двух спиновых состояниях с проекцией спина на направление движения (спиральностью) ±1. В физике фотоны обозначаются буквой γ.

Классическая электродинамика описывает фотон как электромагнитную волну с круговой правой или левой поляризацей. С точки зренияклассической квантовой механики, фотону как квантовой частице свойственен корпускулярно-волновой дуализм, он проявляет одновременно свойства частицы и волны.

Квантовая электродинамика, основанная на квантовой теории поля иСтандартной модели, описывает фотон как калибровочный бозон, обеспечивающий электромагнитное взаимодействие: виртуальныефотоны являются квантами-переносчиками электромагнитного поля и обеспечивают взаимодействие между двумя электрическими или магнитыми зарядами.^[5][6]

Фотон — самая распространённая по численности частица во Вселенной. На один нуклон приходится не менее 20 миллиардов фотонов.^[7]

Уравне́ния Эйнште́йна - уравнения гравитационного поля в общей теории относительности, связывающие между собой метрику искривлённогопространства-времени со свойствами заполняющей его материи. Термин используется и в единственном числе: «уравне́ние Эйнште́йна», так как втензорной записи это одно уравнение, хотя в компонентах представляет собой систему уравнений в частных производных.

Выглядят уравнения следующим образом:

где  — тензор Риччи, получающийся из тензора кривизны пространства-времени посредством свёртки его по паре индексов, R — скалярная кривизна, то есть свёрнутый тензор Риччи,  — метрический тензор,  —космологическая постоянная, а представляет собой тензор энергии-импульса материи, (π — число пи, c — скорость света в вакууме, G —гравитационная постоянная Ньютона).

Уравнение связывает между собой тензоры 4×4, то есть, формально говоря, содержит 16 уравнений. Однако, так как все входящие в уравнения тензорысимметричны, то в четырёхмерном пространстве-времени эти уравнения равносильны 4·(4+1)/2=10 скалярнымуравнениям. Тождества Бьянки приводят к уменьшению числа независимых уравнений с 10 до 6.

В более краткой записи

где  — тензор Эйнштейна, который объединяет тензор Риччи, скалярную кривизну и метрический тензор. Тензор Эйнштейна может быть представлен как функция метрического тензора и его частных производных.

Часто лямбда-член Λg_μν в записи уравнений Эйнштейна принимается равным нулю, поскольку в задачах локальных масштабов, далёких от космологических, он, как правило, мал. Тогда запись ещё более упрощается:

Наконец, при часто использующемся выборе единиц физических величин таким образом, чтобы скорость света и гравитационная постоянная равнялись безразмерной единице, c = G = 1 (т.н. геометризованная система единиц), запись уравнений Эйнштейна становится наиболее простой; в бескомпонентной форме:

Таким образом, уравнение Эйнштейна связывает геометрию пространства-времени (левая часть уравнения) с материей и её движением (правая часть).

Одним из существенных свойств уравнений Эйнштейна является их нелинейность, приводящая к невозможности использования при их решении принципа суперпозиции.

71