Основы математической статистики

1. Выборочный метод.

1. В городе А для определения сроков гарантийного обслуживания проведено исследование величины среднего пробега автомобилей (X), находящихся в эксплуатации в течение двух лет с момента продажи автомобиля магазином. Получен следующий результат (тыс. км): 3,0; 14,4; 25; 18,6; 12,1; 10,6; 18; 17,3; 29,1; 20; 18,3; 21,5; 26,7; 12,2; 14,4; 7,3; 9,1; 2,9; 5,4; 40,1; 16,8; 11,2; 9,9; 25,3; 4,2; 29,6; 25; 20; 14,4; 11,2. Требуется: а) составить ряд распределения частот (вариационный ряд); б) составить ряд распределения относительных частот.

2. По наблюденным данным предыдущей задачи построить многоугольник распределения (полигон частот либо относительных частот).

3. Выборка задана интервальным вариационным рядом:

i	xi < X < xi+1	ni
1	11-14	16
2	14-17	24
3	17-20	30
4	20-23	7
5	23-26	8

Построить гистограммы выборочной оценки плотности вероятности (гистограмму частот и гистограмму относительных частот).

4. Найти числовые характеристики выборки, по данным задачи (1), такие как: размах, моду, медиану, выборочное среднее, выборочную дисперсию, выборочное ср. кв. отклонение.

5. Найти асимметрию и эксцесс по заданному распределению выборки:

	-2	0	1	2
	5	15	30	10

2. Оценка параметров распределения.

1. Найти несмещенную оценку математического ожидания и дисперсии с.в. Х.

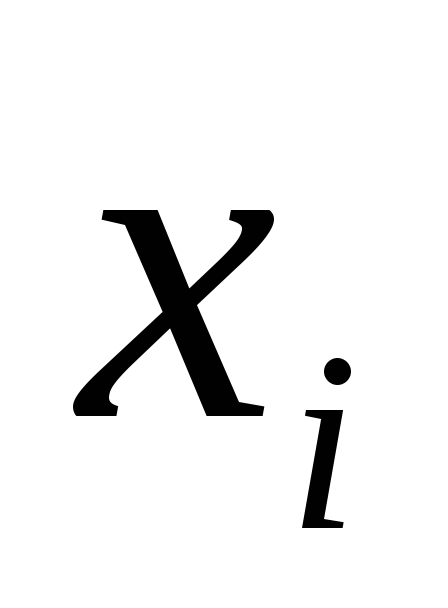
   	- 10	-5	- 1	4
   	25	44	16	15

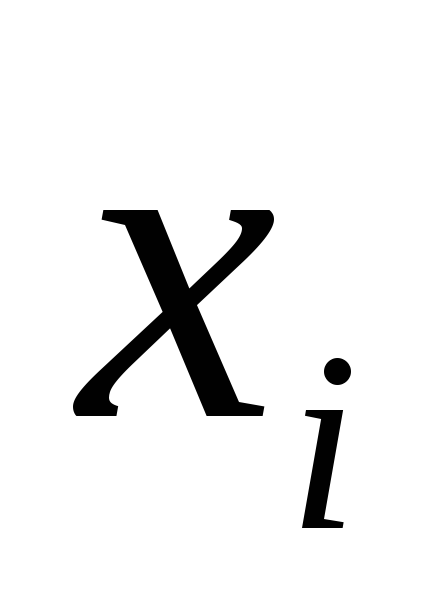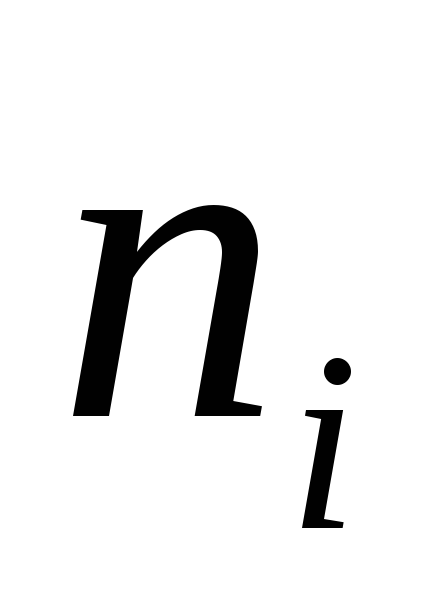2. Случайная величина X (время работы элемента) имеет показательное распределение. Ниже приведено эмпирическое распределение среднего времени работып=200 элементов (в первой строке приведено среднее времяработы элемента в часах; во второй строке указана частота- количество элементов, проработавших в среднем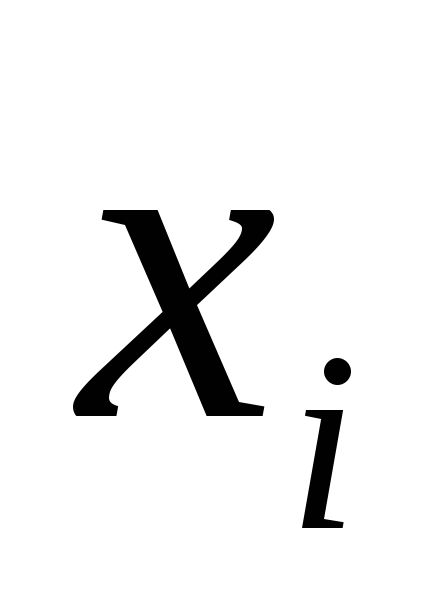часов):

	2,5	7,5	12,5	17,5	22,5	27,5
	133	45	15	4	2	1

Найти методом моментов точечную оценку неизвестного параметра показательного распределения.

3. Случайная величина X (ошибка измерения дальности радиодальномером) подчинена равномерному закону распределения с неизвестными параметрамии.Ниже приведено эмпирическое распределение средней ошибки= 200 измерений дальности (в первой строке указана средняя ошибка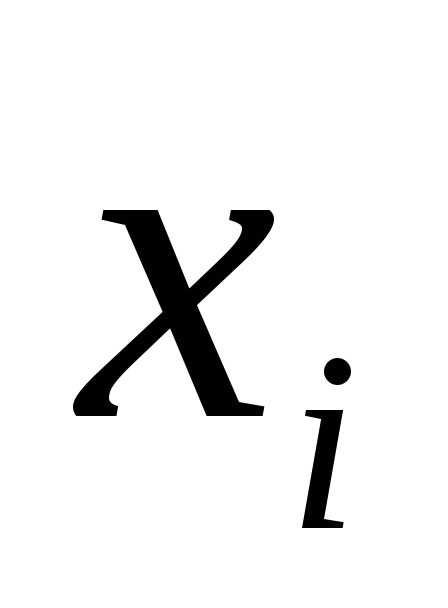; во второй строке указана частота- количество измерений, имеющих среднюю ошибку):

: 3 5 7 9 11 13 15 17 19 21

: 21 16 15 26 22 14 21 22 18 25

Найти методом моментов точечные оценки неизвестных параметров иравномерного распределения.

4. Случайная величина X (число семян сорняков в пробе зерна) распределена по закону Пуассона. Ниже приведено распределение семян сорняков вп= 1000 пробах зерна (в первой строке указано количествосорняков в одной пробе; во второй строке указано- число проб, содержащих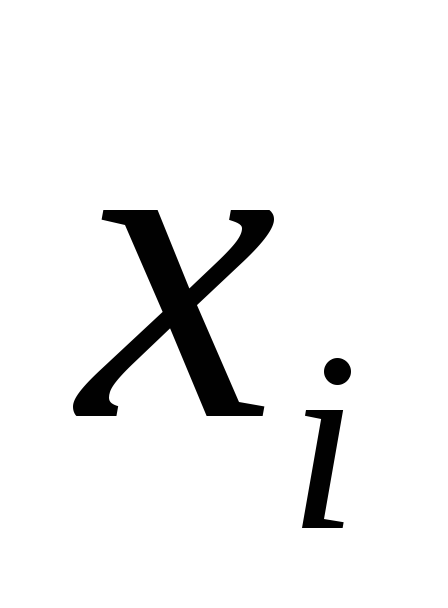 семян сорняков):

	0	1	2	3	4	5	6
	405	366	175	40	8	4	2

Найти методом моментов точечную оценку неизвестного параметра распределения Пуассона .

5. Случайная величина X (отклонение контролируемого размера изделия от номинала) подчинена нормальному закону распределения с неизвестными параметрамии. Ниже приведено эмпирическое распределение отклонения от номинала 200-т изделий (в первой строке указано отклонение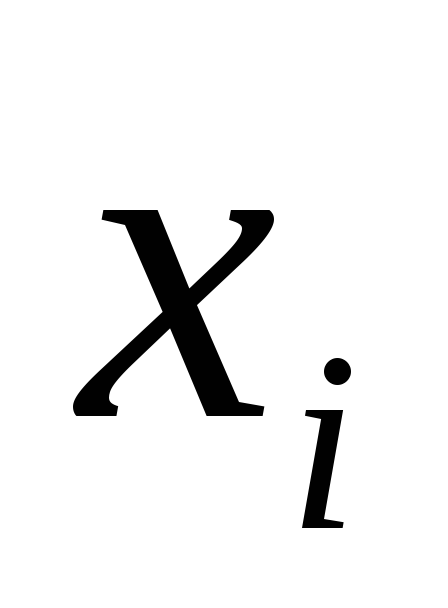- (мм); во второй строке приведена частота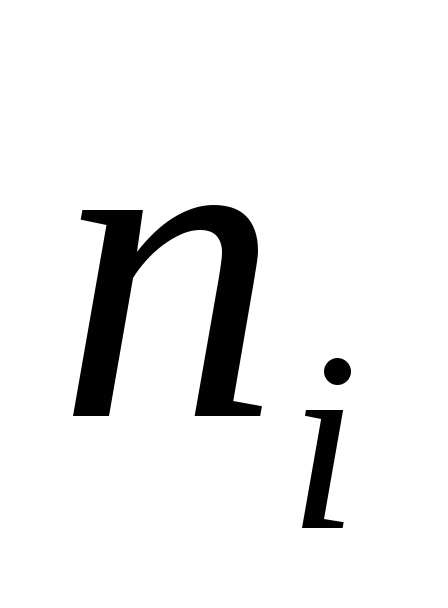- количество изделий, имеющих отклонение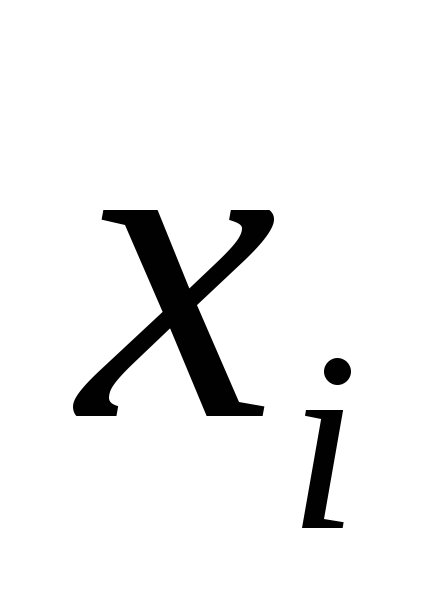):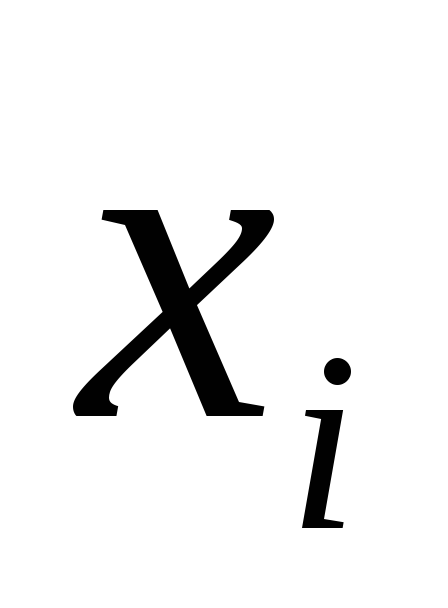0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,2 2,3