- •Гидравлика
- •Поверхностное натяжение.
- •Давление жидкостей.
- •Отстаивание в поле центробежной силы (центрифугирование)
- •Фильтрование
- •Фильтрование с образованием несжимаемого осадка на несжимаемой перегородке
- •Транспорт дисперсных частиц
- •Гидравлическое сопротивление неподвижного слоя при ламинарном режиме движения жидкости.
- •Гидравлическое сопротивление неподвижного слоя при турбулентном режиме движения жидкости
- •Определение скорости начала псевдоожижения
- •I. Перемешивание
- •Констукции мембранных аппаратов
- •Кристаллизация из растворов
- •3.Теплосодержание () влажного воздуха
- •Материальный и тепловой баланс сушки
- •Тепловой баланс простой сушилки
- •Расчет простой сушилки
- •Адсорбция
Поверхностное натяжение.
Работа,
необходимая для образования единицы
поверхности называется межфазным или
поверхностным натяжением
![]() , измеряется в н/м2
в системе СИ. Поверхность раздела между
фазами стремится к минимуму под действием
поверхностных сил, капли имеют форму,
близкую к шару. Поверхностное натяжение
уменьшается с увеличением температуры.
Величина поверхностного натяжения
влияет на смачивание капельными
жидкостями твердых материалов (
фильтрование, адсорбция, конденсация).
, измеряется в н/м2
в системе СИ. Поверхность раздела между
фазами стремится к минимуму под действием
поверхностных сил, капли имеют форму,
близкую к шару. Поверхностное натяжение
уменьшается с увеличением температуры.
Величина поверхностного натяжения
влияет на смачивание капельными
жидкостями твердых материалов (
фильтрование, адсорбция, конденсация).
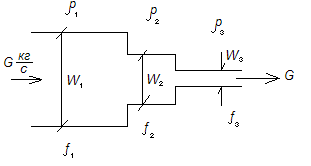
Давление жидкостей.
Давление жидкости на единицу поверхности называется гидростатическим давлением.
р=Р /F,
где Р – сила давления жидкости на поверхность F.
Если жидкость налита в сосуд, то сила давления, действующая на его дно равна весу жидкости в сосуде:
Р=
FН
![]() g,
g,
где F
– площадь дна сосуда, Н – высота столба
жидкости,
![]() плотность жидкости,g
– ускорение свободного падения.
плотность жидкости,g
– ускорение свободного падения.
Следовательно
р=
Н
![]() g,
g,
т.е. давление жидкости на дно сосуда равно весу столба жидкости высотой Н с площадью основания 1м2.
Если давление над жидкостью равно р0 то гидростатическое давление будет равно :
р
= р0
+Н
![]() g.
g.
Давление на вертикальные или наклонные стенки сосуда не является постоянным по высоте стенки, поэтому гидростатическое давление в каждой точке сосуда рассматривается как предел отношения силы давления ΔР к элементарной площади ΔF при F стремящейся к нулю.
р =lim ΔР / ΔF
Давление направлено по нормали к площадке, на которую оно действует одинаково по всем направлениям.
Размерность давления в системе СИ [н/м2 = Па]. Существуют внесистемные единицы измерения давления:
Атм- давление , которое оказывает столб ртути высотой 760 мм, или столб воды высотой 10,33 м = 101 300 н/м2 ( физическая атмосфера).
Ата- давление , которое оказывает столб ртути высотой 735,6 мм или 10 м водного столба = 98 100н/м2 (техническая атмосфера ).
1Па=1 н/м2 = 10-5 бар.
Уравнение расхода и неразрывности потока.
Рассмотрим движение жидкости
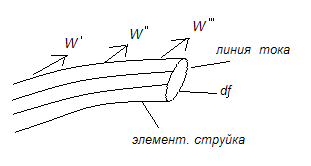
![]()
![]()
![]() -объемный
расход;
-объемный
расход;
G=ρV=ρwf – массовый (весовой) расход, кг/сек., ρ – плотность (кг/м3)
G= ρ1w1f1= ρ2w2f2= … =const, откуда уравнение неразрывности для сжимаемых сред: ρwf =const
Для несжимаемых сред (ρ1= ρ2=… = ρ = const) и имеем:
![]()
 wf
=const
wf
=const
Понятие «сплошная среда»
Силы, действующие в сплошной среде
Массовые силы – силы, пропорциональные массе. Сила тяжести Р =mg. Единичная массовая сила Е.М.С.=
 - сила, отнесенная к единице массы; имеет
размерность ускорения (м/с2).
Проекции единицы массовой силы на оси
координат:X,
Y,
Z.
- сила, отнесенная к единице массы; имеет
размерность ускорения (м/с2).
Проекции единицы массовой силы на оси
координат:X,
Y,
Z.Поверхностные силы – пропорциональны поверхности.
Нормальные поверхностные силы действуют по нормали к поверхности.
Сила давления Р =
рF,
где р - давление [![]() ].
].
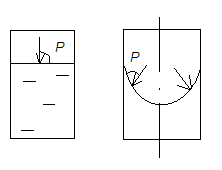
Тангенциальные поверхностные силы действуют по касательной к поверхности.
Сила трения (согласно закону Ньютона)
Ртр=
- μFтр![]()

Вывод основного уравнения гидродинамики
Основное уравнение гидродинамики характеризует перенос количества движения (импульса) в сплошной среде (жидкости (газе)).
Основной задачей при анализе переноса импульса является определение закономерностей (зависимостей):
p=f(x, y, z, τ); w=φ(x, y, z, τ) – нестационарный режим
p=f(x, y, z,); w=φ(x, y, z,) – стационарный режим.
Рассматриваем баланс сил в отсутствии источников количества движения в элементарном объеме dV=dxdydz
![]()
![]()
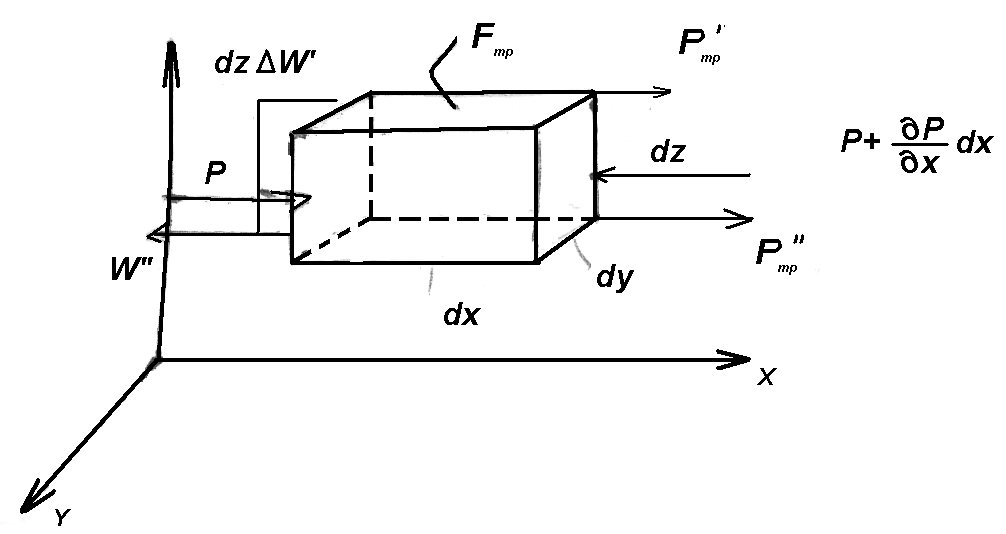
Массовые силы (вопрос о ее направлении решается в каждом конкретном случае).
Тогда (ЕМС)x=X=![]() ,
откуда
,
откуда
X·m=Xρdxdydz
Нормальные поверхностные силы (силы давления)
pdydz
– (p+![]() dydz=
-
dydz=
-
![]()
Тангенциальные поверхностные силы (силы трения).
Рассматриваем верхнюю и нижнюю грани
Hx= τH·dxdy - τв·dxdy, где dxdy=dfтр
![]() ;
;
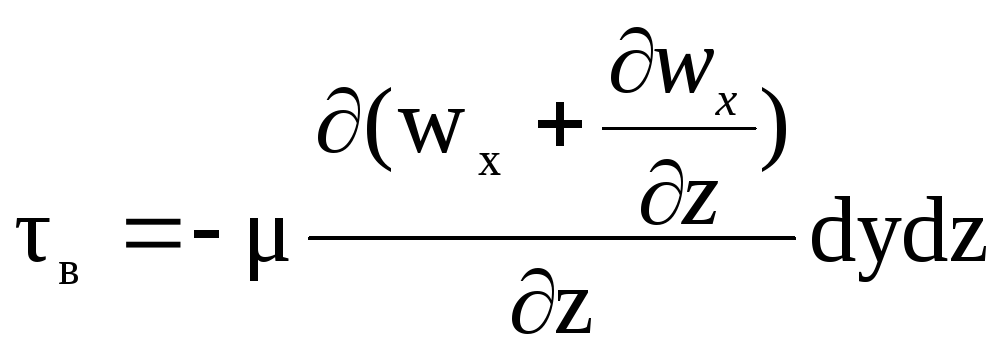 ;
;
Тогда Hx:
τH·df
– τв·df=
=![]() +
+![]() +
+ =
=
(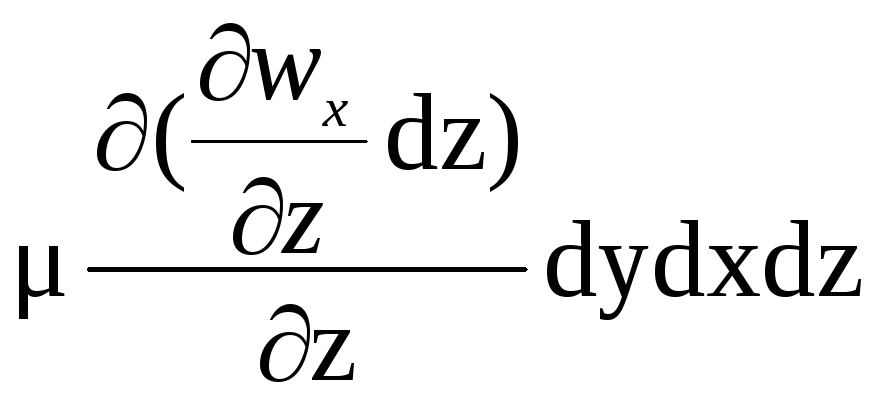 -
-![]() )
)
=μ (![]() +
+![]() +
+![]() )dx
dy
dz=μ
)dx
dy
dz=μ![]() wx
dx
dy
dz
wx
dx
dy
dz
В соответствии со
вторым законом Ньютона результирующая
массовых и поверхностных сил равна силе
инерции, т.к.
![]() .
.
В нашем случае
X
ρ
dx
dy
dz
-
![]() dx
dy
dz
+
dx
dy
dz
+
![]() dx
dy
dz
= Fин
dx
dy
dz
= Fин
Fин=ma=ρ
dx
dy
dz
![]() ,
где а =
,
где а =![]() - ускорение, тогда:
- ускорение, тогда:
X
ρ
dx
dy
dz
-
![]() dx
dy
dz+
dx
dy
dz+
![]() =ρ
dx
dy
dz
=ρ
dx
dy
dz
![]()
разделим уравнение
на (ρ
dx
dy
dz)
и учитывая, что ν =![]() преобразуем уравнение в следующий вид:
преобразуем уравнение в следующий вид:
![]() =Х
+
=Х
+![]() -
-
![]()
![]() =У+
=У+![]() -
-
![]()
![]() Система
уравнений Навье - Стокса
Система
уравнений Навье - Стокса
![]() =Z+
=Z+![]() -
-
![]()
Необходимо иметь в виду, что wx – функция координат и времени, аналогично для wy wz.
Полный дифференциал равен:
dwx=![]() dτ+
dτ+![]() dx+
dx+![]() dy+
dy+![]() dz
,
dz
,
имея в виду, что
![]() =
wx;
=
wx;
![]() =
wy;
=
wy;
![]() =
wz
=
wz![]() ,
,
делим каждое
слагаемое уравнения на ![]() :
:
![]() =
=![]() +
+![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]() +wx
+wx![]() +wy
+wy![]() +wz
+wz![]()
и аналогично для
![]() и
и![]()
Основы теории гидродинамического подобия:
Существует геометрическое подобие, подобие физических параметров, временное подобие, подобие действующих сил.
Рассмотрим движение реальной жидкости под действием силы тяжести,
то есть движение вдоль оси Z.
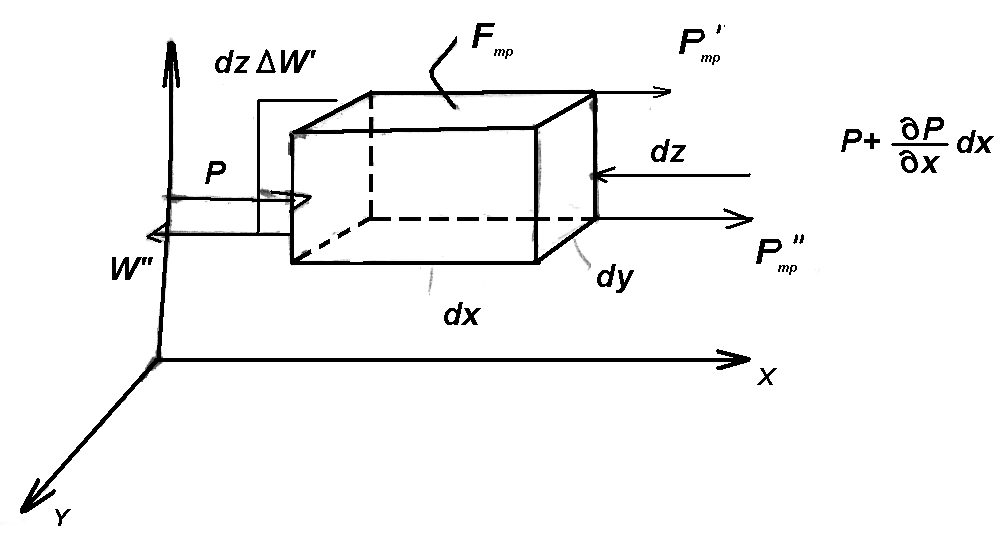
Z-![]()
![]() +ν(
+ν(![]() wz)=
wz)=
![]() ,
,
![]() =
=![]() +wx
+wx![]() +
wy
+
wy![]() +
wz
+
wz
![]()
В нашем случае
равномерное однонаправленное движение
вдоль оси Z
, значит ускорение а =
![]() =
0, wx
= wy=
0, уравнение можно записать :
=
0, wx
= wy=
0, уравнение можно записать :
![]() =
wz
=
wz![]() =
=![]() и тогда
и тогда
Z
-
![]()
![]() +ν(
+ν(![]() wz)
=
wz)
=
![]() ;
×dz
, тогда
;
×dz
, тогда
Zdz-![]()
![]() dz+ν(
dz+ν(![]() wz)
dz
=
wz)
dz
=
![]() ,
,
так как движение вдоль оси Z происходит под действием силы тяжести,
то Z= -g
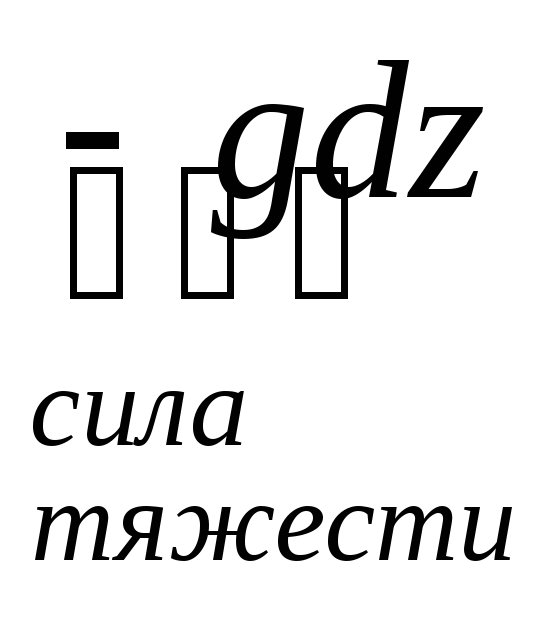
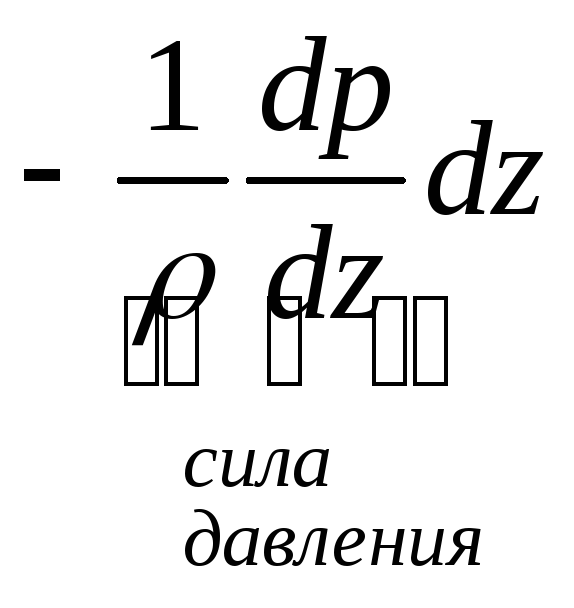 +
+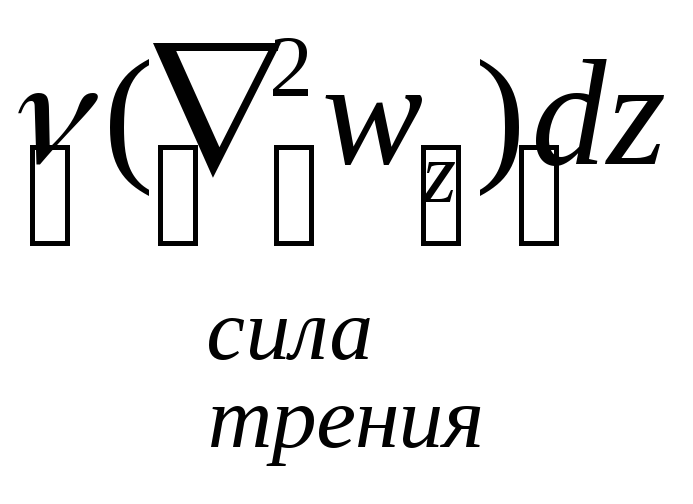 =
=
![]() :
: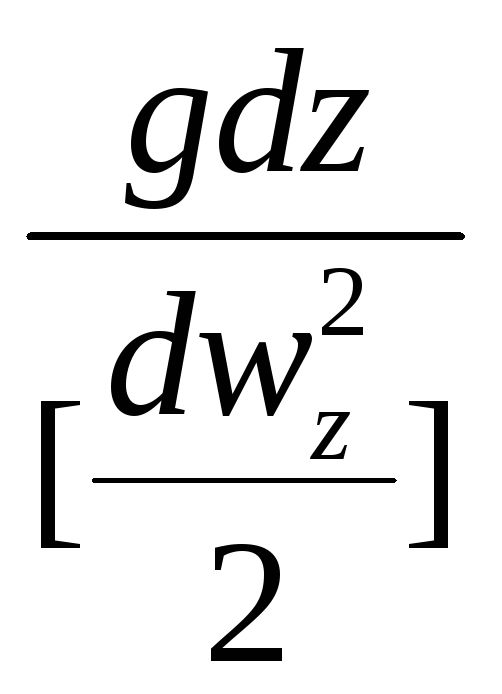 →
→![]()
![]() (критерий Фруда)
(критерий Фруда)
![]() :
: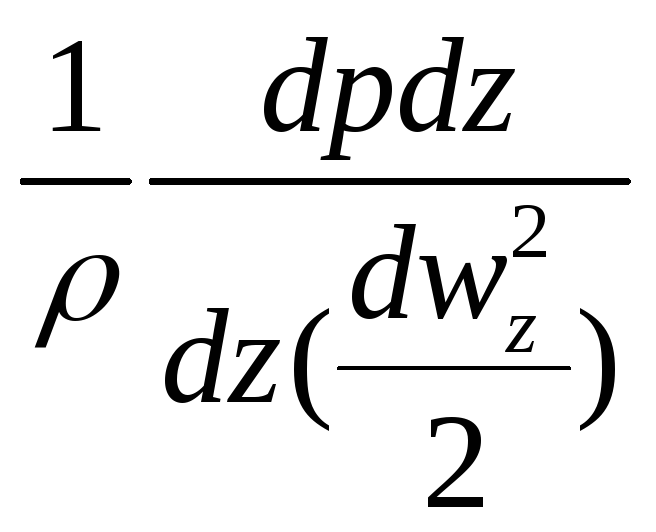 →
→![]() →
→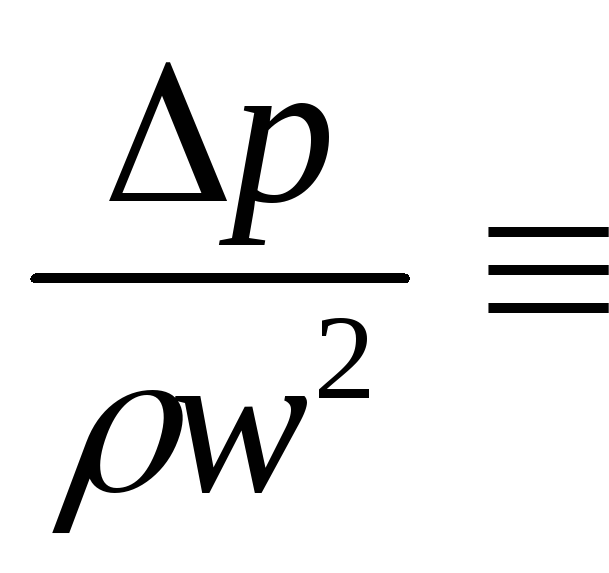 Eu
(критерий Эйлера)
Eu
(критерий Эйлера)
![]() :
: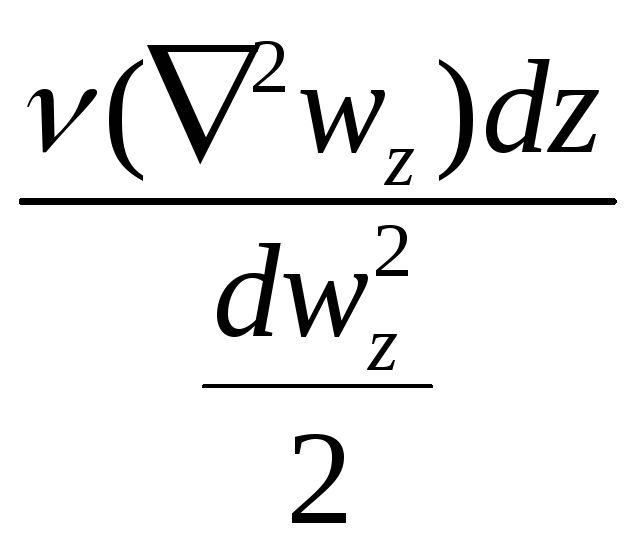 →
→![]() →
→![]() →
→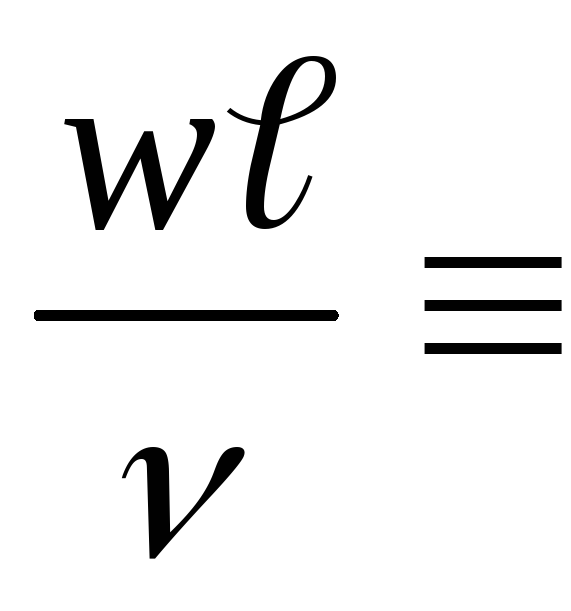 Re
(критерий Рейнольдса)
Re
(критерий Рейнольдса)
Таким образом, получено общее критериальное уравнение гидродинамики
-
![]() -
-![]() +
+![]() =1
или –Fr
- Eu
+
=1
или –Fr
- Eu
+![]() =1.
=1.
Определяемым критерием является Eu (т.к. нас интересует Δр); определяющими Re и Fr, поэтому уравнение Навье - Стокса в критериальном виде можно записать:
Eu=![]() –Fr–1,
Eu=f(Re,
Fr)
–Fr–1,
Eu=f(Re,
Fr)
Cочетание базовых критериев подобия, позволяет получить новые критерии, так например :
Re2
Fr=![]()
![]() =
=![]() →Ga=
→Ga=![]() - критерий Галилея
- критерий Галилея
Ga![]() =
=![]()
![]() →
Ar=
→
Ar=![]()
![]() - критерий Архимеда
- критерий Архимеда
Уравнение Бернулли
Для однонаправленного равномерного движения под действием силы тяжести Уравнение Навье – Стокса имеет вид:
![]() +
ν(
+
ν(![]() wz)=
wz)=![]() ,
,
где Лаплассиан
![]() wz=
wz=![]() +
+![]() +
+![]() .
.
Распределение
скоростей wz
по осям не известно, поэтому вводим
понятие «идеальная
жидкость», для которой
![]() =0.
=0.
Тогда
![]()
![]() =0
, разделим обе части на
=0
, разделим обе части на ![]()
![]()
![]() =
0;
=
0;
откуда для идеальной жидкости
![]()
![]() =0
=0
Для реальной жидкости уравнение Бернулли имеет вид
![]()
![]() =
=![]()
![]() +
hп,
где hп
– потерянный напор.
+
hп,
где hп
– потерянный напор.
Вывод уравнения Дарси-Вейсбаха

Баланс сил:
![]()
![]() Ртр=0
Ртр=0
Δ![]() Ртр=0,
Ртр=0,
где Ртр=τтрFтр=τтр![]()
Δ![]() τтр
τтр![]() =0→
Δ
=0→
Δ![]() =
=![]()
hп=![]()
![]() .
.
Приняли, что
![]() ~
~![]() ,
тогдаhп~
,
тогдаhп~![]()
![]()
Ввели коэффициент пропорциональности λ – коэффициент гидравлического сопротивления.
hп
= λ![]()
![]() - уравнение равномерного движения
реальной жидкости, уравнение Дарси-Вейсбаха.
- уравнение равномерного движения
реальной жидкости, уравнение Дарси-Вейсбаха.
Тогда уравнение Бернулли для реальной жидкости принимает вид:
![]()
![]() =
=![]()
![]() +λ
+λ![]()
![]()
Для ньютоновской жидкости
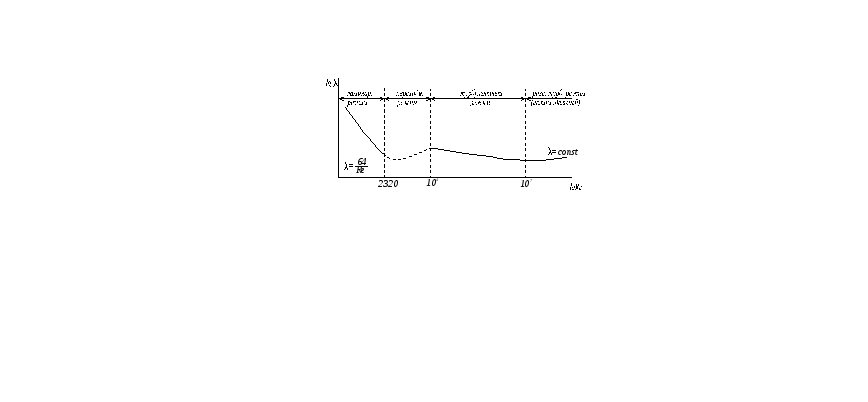
![]()
![]()
![]()
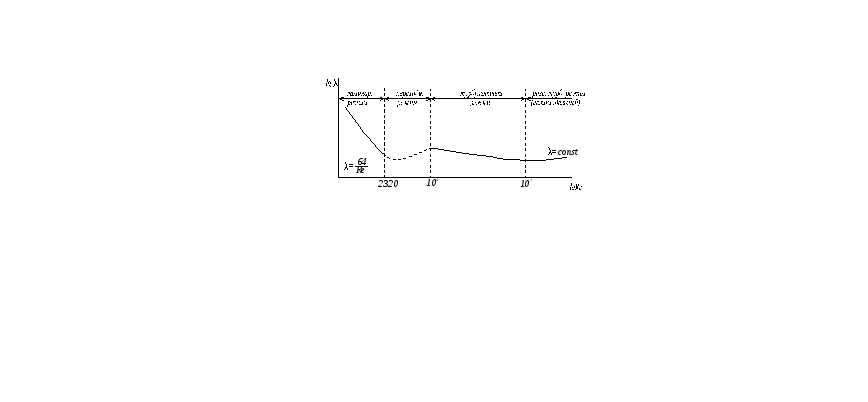
при ламинарном
режиме: Re2300
λ=![]() ,
,
Re=104-105
λ=![]() - формула Блазиуса
- формула Блазиуса
Re=105-3,4·106 λ=0,0032+0,221·Re-0,237 – формула Никурадзе
Re=104-2·107 λ=0,16/ Re0,16 – формула Женеро.
Для турбулентного
режима
![]() =2
=2![]() - 0,8;
- 0,8;![]() =
- 2
=
- 2![]()
Для автомодельного
режима
![]() =2
=2![]() ,
где
,
где![]() ;s
– высота выступов шероховатости (для
новых стальных труб s=0,1мм,
старых – 2мм; для чугунных s=0,25мм)
;s
– высота выступов шероховатости (для
новых стальных труб s=0,1мм,
старых – 2мм; для чугунных s=0,25мм)
Применение Уравнения Бернулли
Расчёт простого трубопровода
|
|
|
Уравнение Бернулли для реальной жидкости
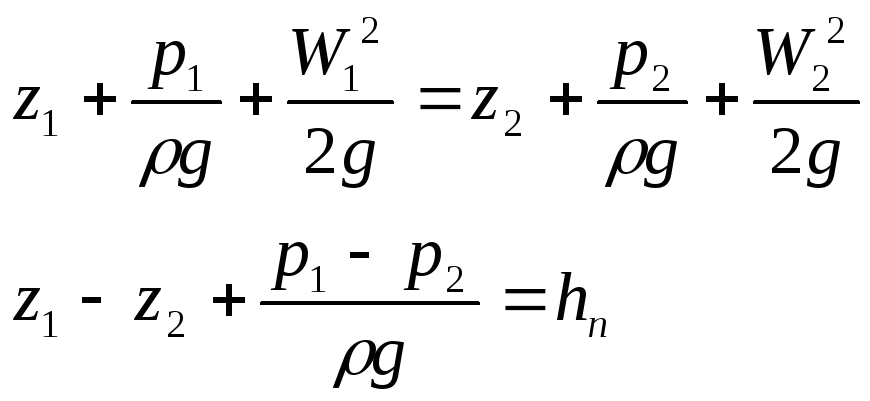
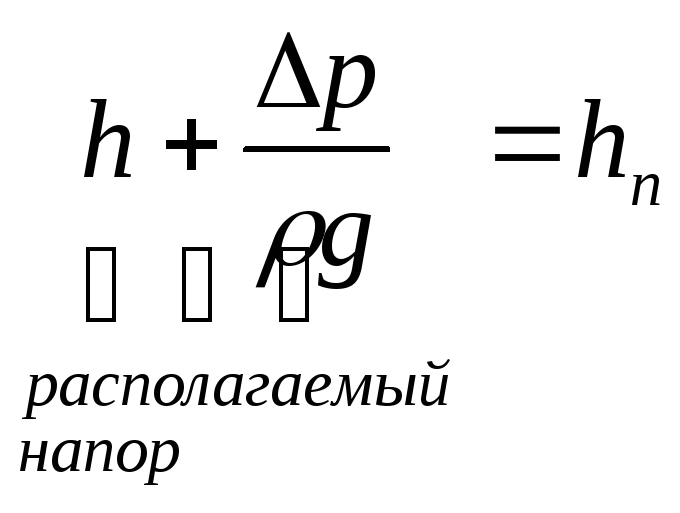
Н- располагаемый
напор, если
![]() - движение возможно
- движение возможно
![]() ,
где
,
где![]() -
гидравлическое сопротивление прямых
участков
-
гидравлическое сопротивление прямых
участков
![]() - гидравлическое
сопротивление фасонных частей
- гидравлическое
сопротивление фасонных частей
![]() - справочная
величина
- справочная
величина
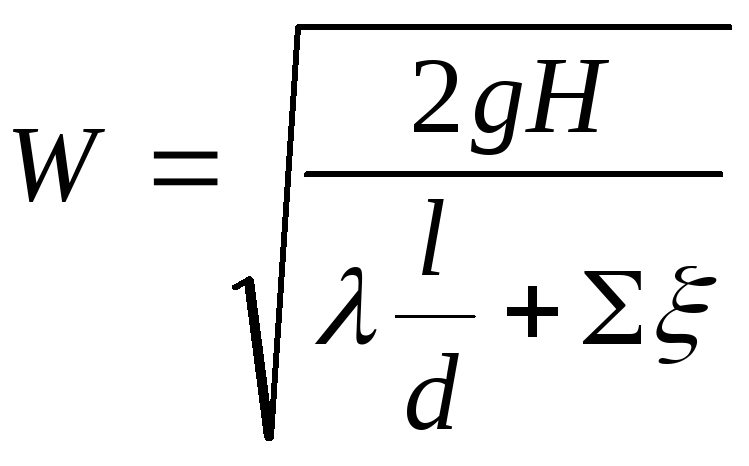 - скорость движения
жидкости
- скорость движения
жидкости
Для длинных трубопроводов
![]() , тогда
, тогда
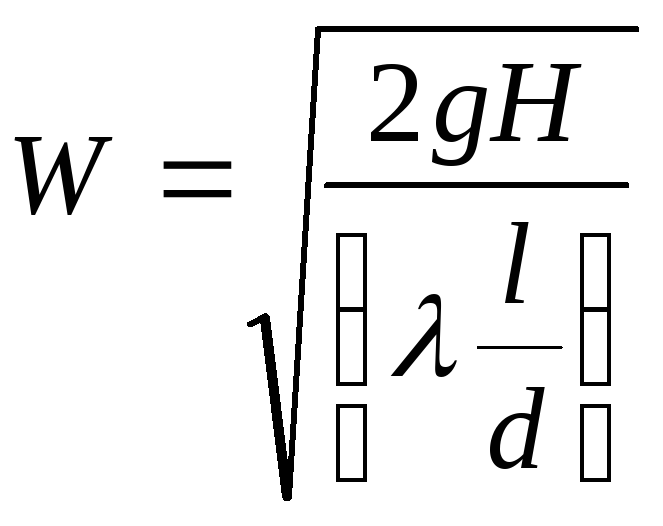
Расход
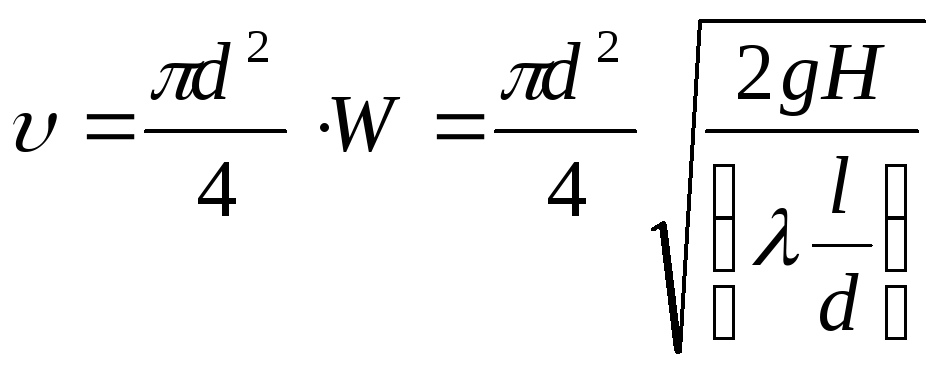
1. Задан расход
![]() определитьd
или задан d
– определить расход
определитьd
или задан d
– определить расход
![]()
![]()
![]() - гидравлический
уклон – потери напора на 1 м трубопровода
- гидравлический
уклон – потери напора на 1 м трубопровода
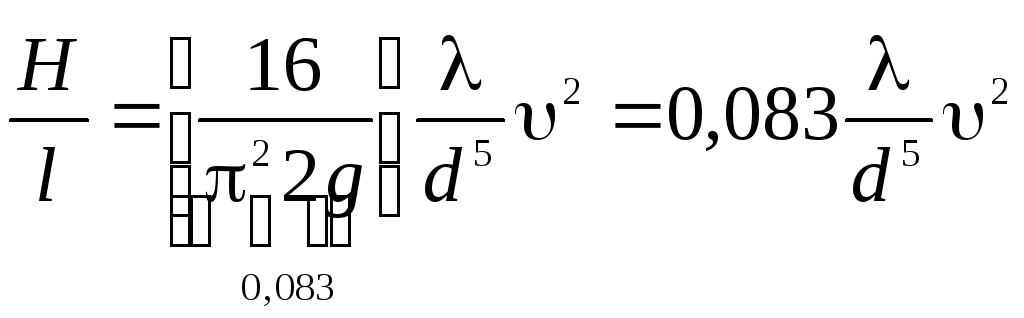
Трубопровод с непрерывным путевым и транзитным расходом
Для простого трубопровода известно, что
w=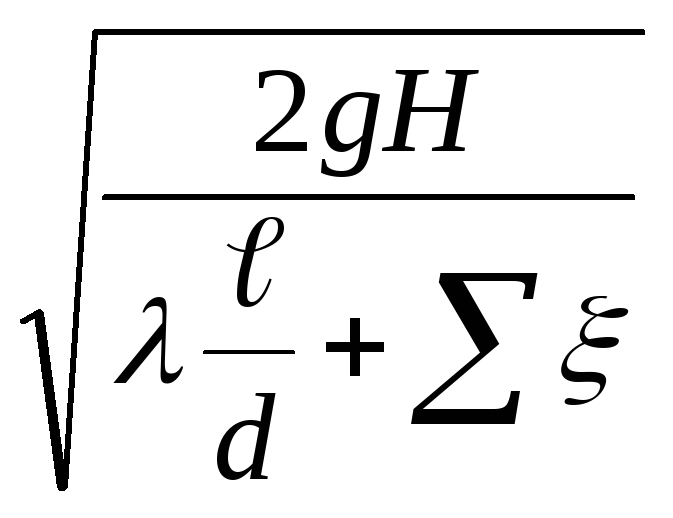 и υ =
и υ =![]()
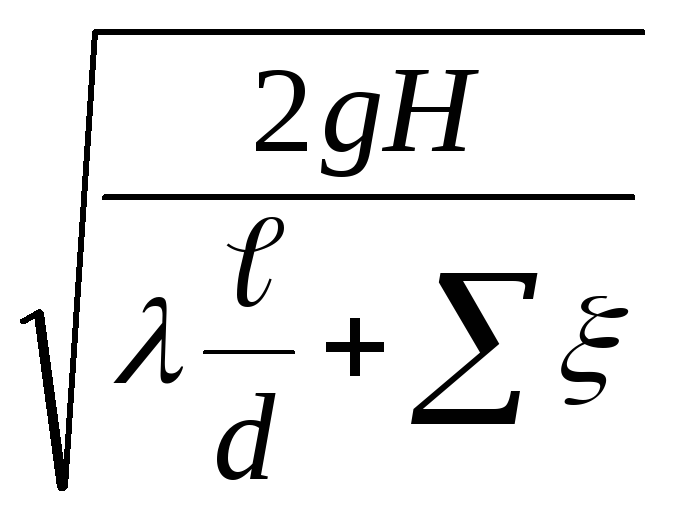
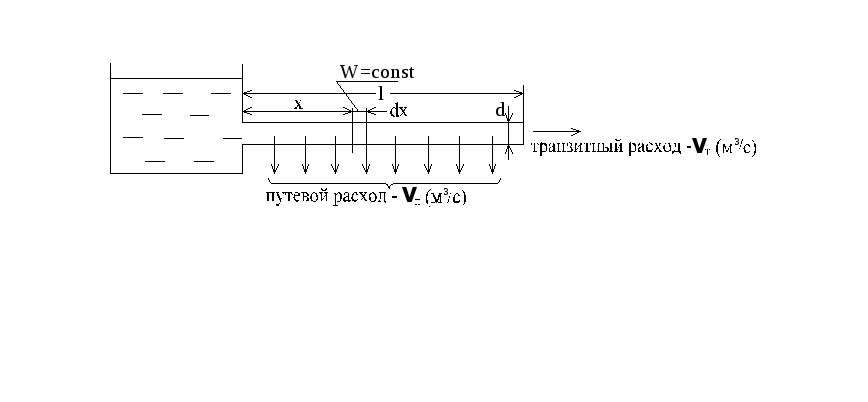
Если на единице
длины трубопровода должно отводиться
υ[![]() ],
то путевой расход υп=υ
],
то путевой расход υп=υ![]() .
.
Иногда требуется, чтобы из последнего сечения уходил дополнительный поток υт – транзитный.
Следовательно, суммарный расход равен (υп+ υт).
Суммарный поток
по длине
![]() меняется, тогда на участкеdx
имеем
меняется, тогда на участкеdx
имеем
dhn=λ(![]() )
)![]()
![]() и
и
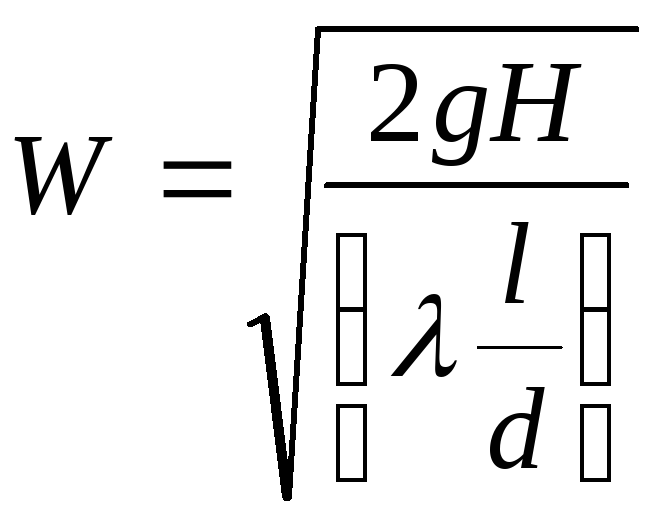
Так как на всем
отрезке пути было х отводов с расходом
υ[![]() ],
то общий расход равен
],
то общий расход равен ![]() ,
скорость равна:
,
скорость равна:
w=![]() ,т.е.
,т.е.
dhn=![]()
![]() dx
dx
hn
=![]()
![]()
![]() =
=![]()
![]()
hn=![]()
![]()
В частном случае,
когда υт=0
и hn=![]()
![]()
Когда υп=0
→ hn=![]()
![]()
Истечение жидкости через отверстия
I. истечение при h =const
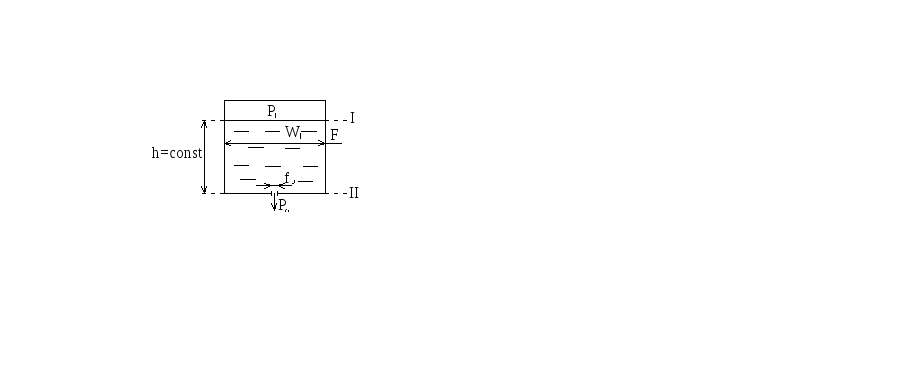
![]()
![]() =
=![]()
![]() +hп
+hп
(Z1-Z2)=Н;
![]() =
=![]()
Н=
![]() -
-
![]() +hп
+hп
![]()
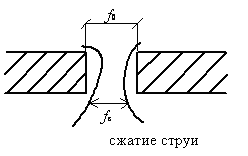
Истечение из бокового отверстия
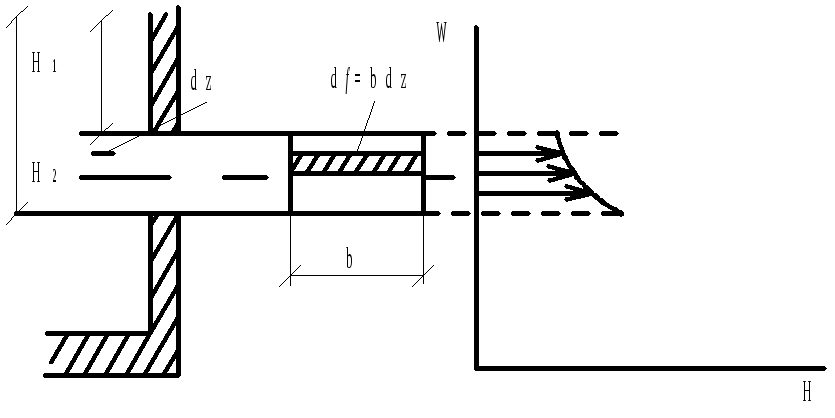
[![]() +h]=
+h]=
![]()
f0w2=Fw1;
w1=![]() w2
w2
Н=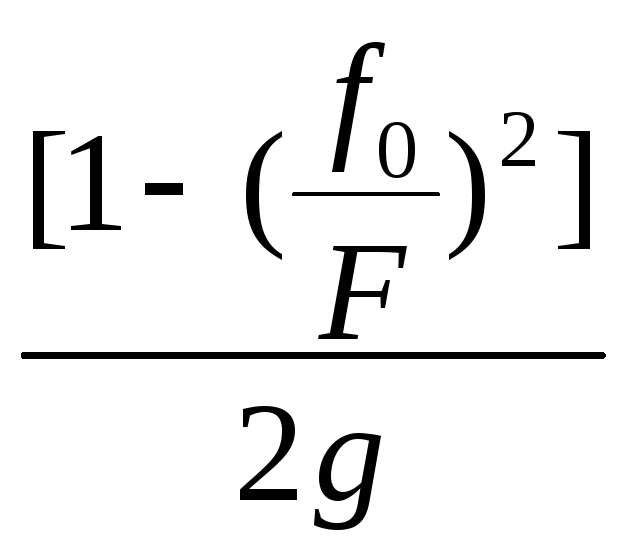 w2+hn;
где hn=
w2+hn;
где hn=![]()
![]()
2gH=[1-(![]() )2]
w2+
)2]
w2+
![]() w2
или
2gH=(1+
w2
или
2gH=(1+![]() )
w2
)
w2
w=![]()
![]() →
w=
→
w=![]()
![]()
υ=![]() 0w→
υ
=
0w→
υ
=![]()
![]()
![]() 0
0![]() ;
;![]()
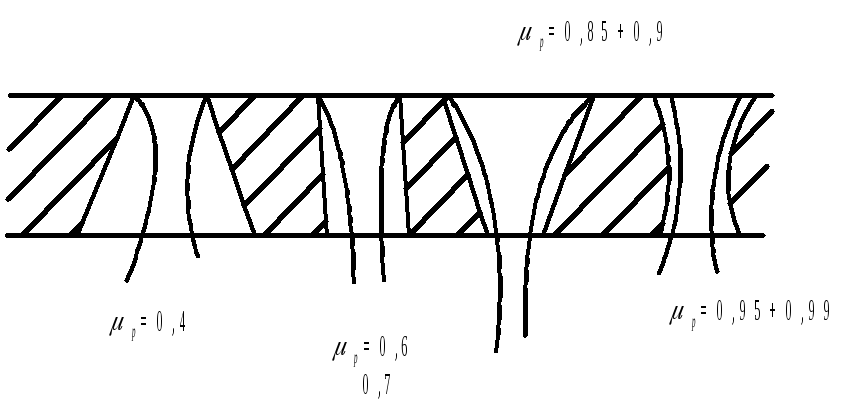
![]() =μp
→ υ
= μp
=μp
→ υ
= μp
![]() 0
0![]()
Истечение через водослив
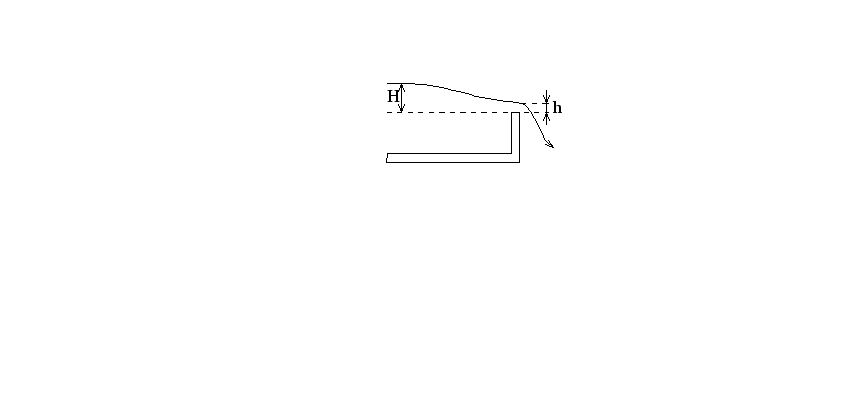
![]() =
=![]()
![]() =
=![]()
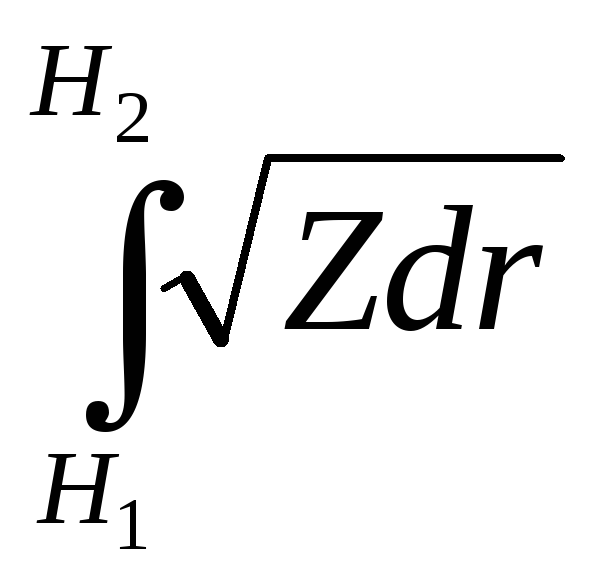
![]() =
=![]()
![]() b
b![]() (H
(H![]()
![]() -H
-H![]()
![]() )
)
![]() =
=![]() bh
bh![]()
Опыт показывает, что толщина струи под порогом соответствует максимальному расходу.
Следовательно,
![]() =0
=0
![]() =
=![]() b
b![]() (
(![]() -
-![]() )=0,
)=0,
но
![]() b
b![]()
![]() 0.
0.
Тогда
![]() =
=![]() ;
(H-h)=
;
(H-h)=![]() ;H=
;H=![]() h
или h=
h
или h=![]() H
H
Тогда
![]() =
=![]() b
b![]()
![]() =
=![]() b
b![]()
![]()
![]() или
или
![]() =
=![]()
![]() b
b![]() H
H![]()
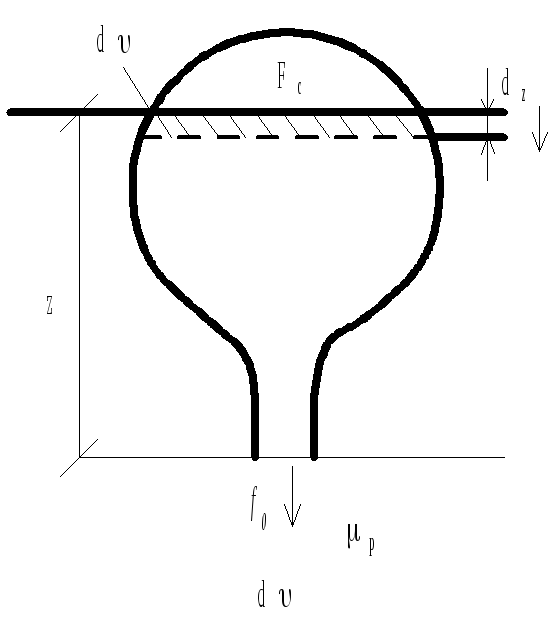
Опорожнение (истечение при переменном уровне)
За время
![]() :
:
-d![]() =Fcdr(м3)
=Fcdr(м3)
d![]() =
=![]() f0
f0![]()
![]() (м3)
(м3)
-Fcdr=![]() f0
f0![]()
![]() ,
откуда
,
откуда
![]() =
=![]() =-
=-![]()
![]()

![]()
|
|
![]()

Истечение из донных отверстий при постоянном напоре

![]() - скорость перемещения слоёв в сосуде
- скорость перемещения слоёв в сосуде
![]() - скорость истечения
- скорость истечения
![]() ;
;
![]() ;
;
![]()
|
|
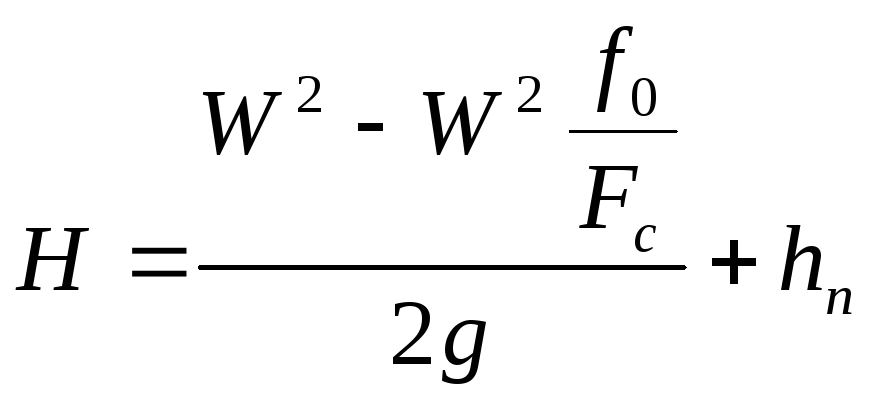
![]()
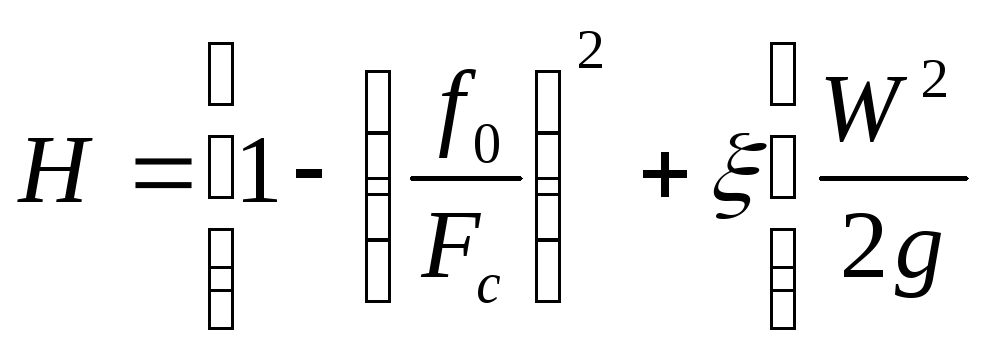
![]()
![]()

![]()
![]()
|
|
|
![]()
![]() - к-т расхода
- к-т расхода
![]()
![]()
|
|
Характеристика реальных жидкостей.
Ньютоновские жидкости.
1.Сила трения между
слоями жидкости может быть выражена
уравнением:
![]() =μFтр
=μFтр![]() , откуда
, откуда
![]() =τтр=μ
=τтр=μ![]() ,
,
где τтр
– напряжение сдвига (касательное);
![]() - градиент сдвига; μ-вязкость
- градиент сдвига; μ-вязкость
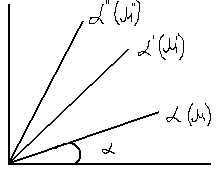
τтр
![]() ;
;![]()
![]()
τтр=μк(![]() )а,
а=1 для ньютоновской жидкости
)а,
а=1 для ньютоновской жидкости
Неньютоновские жидкости. Бингамовские жидкости
τтр=μк(![]() )а
τтр=
τ0+μн(-
)а
τтр=
τ0+μн(-![]() )
)
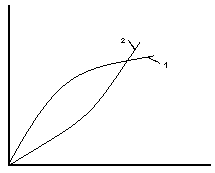
![]()
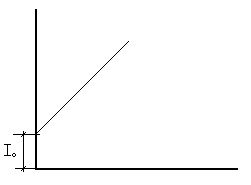
![]()
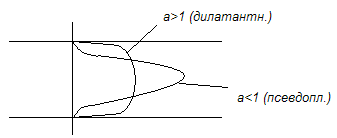
Бингамовские жидкости- осадки
2 – псевдопластичные a<1,разбавленные суспензии
1 – дилатантные a>1, концентрированные суспензии
2. Режимы движения реальных жидкостей
Ламинарный параллельно-струйчатый режим

Турбулентный (вихревой) режим
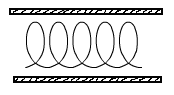
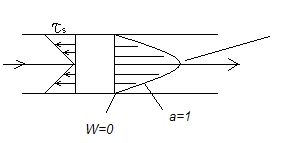
Законы ламинарного режима.
2.1 Распределение касательного напряжения трения τтр
Ртр=
μк(![]() )аFтр,
откуда
)аFтр,
откуда
τтр=![]() =μк(
=μк(![]() )а
)а
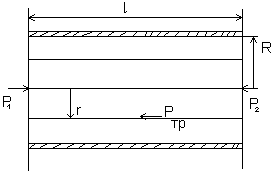
Баланс сил Δр![]() -
τтрFтр=0;
-
τтрFтр=0;
Δр![]() =τтр
=τтр![]() ,
откуда
,
откуда
τтр=![]()
при r =0→τтр=0
при r
=R→
τтр=![]() =
τmax=
τs
=
τmax=
τs
2.2 Распределение скорости по сечению круглой трубы.

τтр=![]()
μк(![]() )а
=
)а
=
![]() ;
;
(![]() )а
=
)а
=![]()
![]() = [
= [![]() →
→![]()
![]() +[
+[![]()
![]()
![]()
![]()
![]() =
=![]() [
[![]()
![]() (
(![]() )
)
Для ньютоновских
жидкостей а=1 и
![]() :
:
![]() =
=
![]() (
(![]() )
параболическое распределение
)
параболическое распределение ![]() =f(r)
=f(r)
При этом
![]()
![]() [
[![]()
![]()
![]() ;
;
для ньютоновских
жидкостей (а=1,
![]() )
)
![]() мах=
мах=![]()
2.3.Расход и средняя скорость
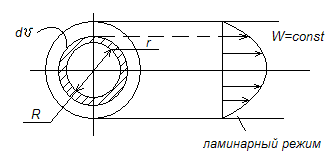
Изменение расхода
dυ=![]() df,
где df=2πrdr-площадь
колечка
df,
где df=2πrdr-площадь
колечка
![]() =
=![]() [
[![]()
![]() (
(![]() )
)
dυ=![]() [
[![]()
![]() (
(![]() )2πrdr
)2πrdr
![]() [
[![]()
![]()
![]() (
(![]() )r
dr
)r
dr
![]()
![]() rdr
=
rdr
=
![]()
![]() R2=
R2=![]()
![]() =
=![]()
![]()
![]()
![]() rdr
=
rdr
=![]()
![]() dr
=
dr
=![]()
![]()
![]() (
(![]() )dr
= (
)dr
= (![]()
![]() )
)![]() =
=![]()
![]() =
=![]()
![]()
υ =
![]() [
[![]()
![]()
![]() =
=![]() [
[![]()
![]()
![]()
Для ньютоновских
жидкостей (а=1,
![]() )
)
υ=![]()
![]() - уравнение Пуазейля-Гагена
- уравнение Пуазейля-Гагена
Средняя скорость для ньютоновских жидкостей:
![]() ср=
ср=![]() =
=![]() =
=![]()
![]() ,
,
![]() мах=
мах=![]() , тогда
, тогда![]() =
=![]()
Средняя скорость для неньютоновских жидкостей:
![]() ср=
ср=![]() [
[![]()
![]()
![]()
2.4 Коэффициент гидравлического сопротивления:
Для средней скорости ньютоновской жидкости имеем
![]() ср
=
ср
=![]()
![]() =
=![]()
![]() =
=![]()
Re=![]() →
→![]()
![]() ;
;
![]() =
=![]()
![]() =
=![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
hn=![]() =
=![]()
![]()
![]() ,
,
λ=![]()
Для неньтоновской жидкости:
λ=![]() ,
где Re(н.ж.)=
,
где Re(н.ж.)=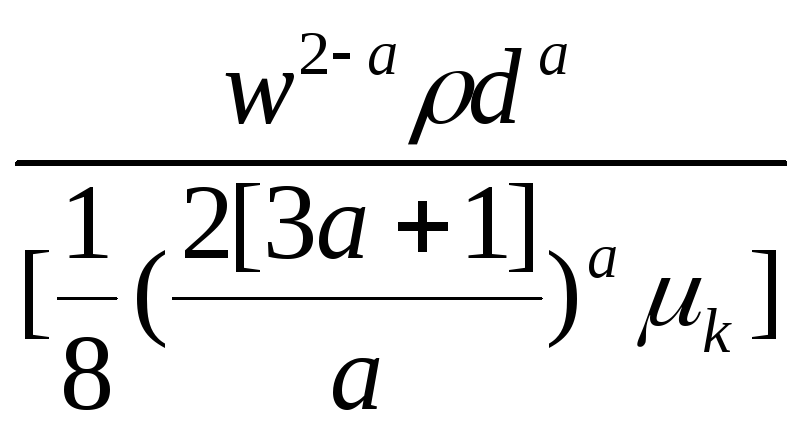
![]()
![]()
![]()
hn=![]() =λ
=λ![]()
![]() ;
;
![]() =
=![]()
![]() ,
т.е.Eu=
,
т.е.Eu=![]() ,Eu=
,Eu=![]()
Бимгамовские жидкости
Рассмотрим движение ламинарного потока и стержнеподобного ядра потока
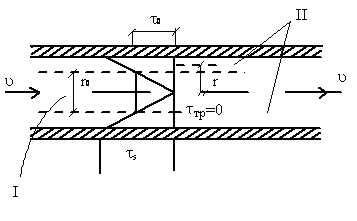
Для ламинарного потока: r>r0 и τтр> τ0
![]() Ртр=Fтр
τтр=
Ртр=Fтр
τтр=![]() ,
откуда
,
откуда
![]()
![]()
![]() =
=![]()
![]() ;
;
![]() =
=![]()
![]() - τ0;
- τ0;
![]() =
=![]() (
(![]()
![]() - τ0);
- τ0);
![]()
![]() =
=![]() [
[![]()
![]() - τ0
- τ0![]() ]
приr0
]
приr0![]() r
r![]() R
R
![]() =
=![]() [
[![]() (R2-r2)
- τ0(R-r)]
(R2-r2)
- τ0(R-r)]
Видно, что при τ0=0 → имеем распределение w=f(r) для ньтоновской жидкости.
![]() =
=![]() [
[![]() (R2-r2)
(R2-r2)
Скорость стержня (при r = r0):
![]() ст=
ст=![]() [
[![]() (R2-r02)
- τ0(R-r0)]
(R2-r02)
- τ0(R-r0)]
Расход бингамовской жидкости
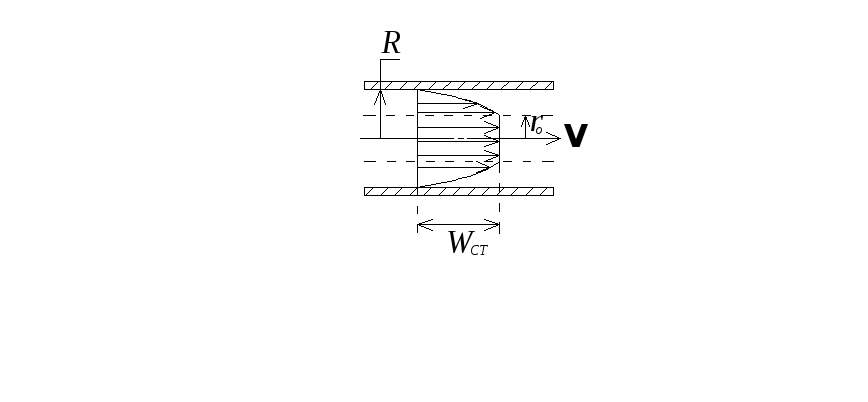
υ= υст+ υкольц.сеч.
υ=πr02
![]() ст+
ст+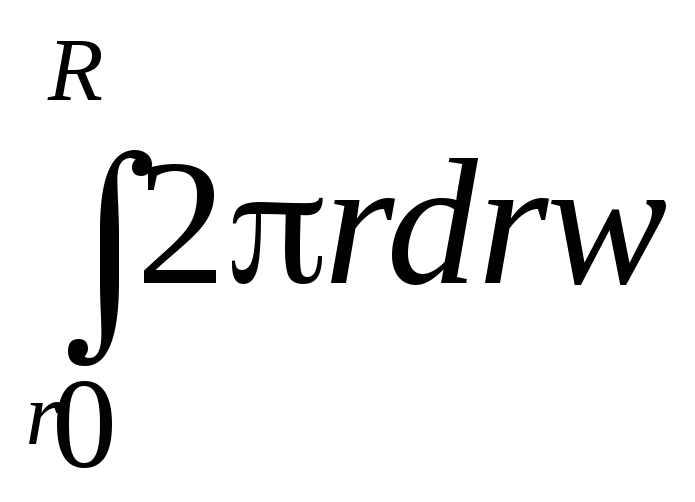 =πr02
=πr02
![]() ст+2π
ст+2π![]()
![]() [
[![]() (R2-r2)
- τ0(R-r)]rdr=
(R2-r2)
- τ0(R-r)]rdr=
= πr02
![]() ст+
ст+![]()
![]() (R2-r2)rdr
-
(R2-r2)rdr
-
![]()
![]() (R-r)rdr
(R-r)rdr
![]() R2rdr
-
R2rdr
-
![]() r3dr
= R2
r3dr
= R2![]() rdr
-
rdr
-![]() r3dr
= R2(
r3dr
= R2(![]()
![]() )
- (
)
- (![]()
![]() )
)
![]() Rrdr
-
Rrdr
-
![]() r2dr=
R(
r2dr=
R(![]()
![]() )
- (
)
- (![]()
![]() )
)
После интегрирования
и подстановки значений ![]() ст
, τ0=
ст
, τ0=![]() r0,
r0=
r0,
r0=![]() и имеем:
и имеем:
υ=![]() [1-
[1-![]()
![]()
![]()
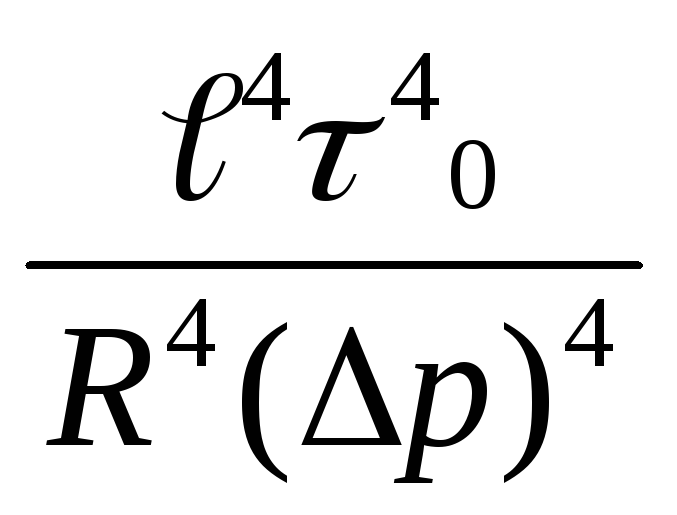 ],откуда
],откуда
![]() ср=
ср=![]() =
=![]() [1-
[1-![]()
![]()
![]() (
(![]() )4]
)4]
Коэффициент гидравлического сопротивления
![]() +
+![]() =
=![]() +
+![]() ,
т.е. λ=f(Re=
,
т.е. λ=f(Re=![]() ),
гдеC=
),
гдеC=![]() .
.
Пленочное движение жидкостей
Рассмотрим гравитационное движение ньютоновской жидкости вдоль вертикальной стенки (движение только под действием силы тяжести)
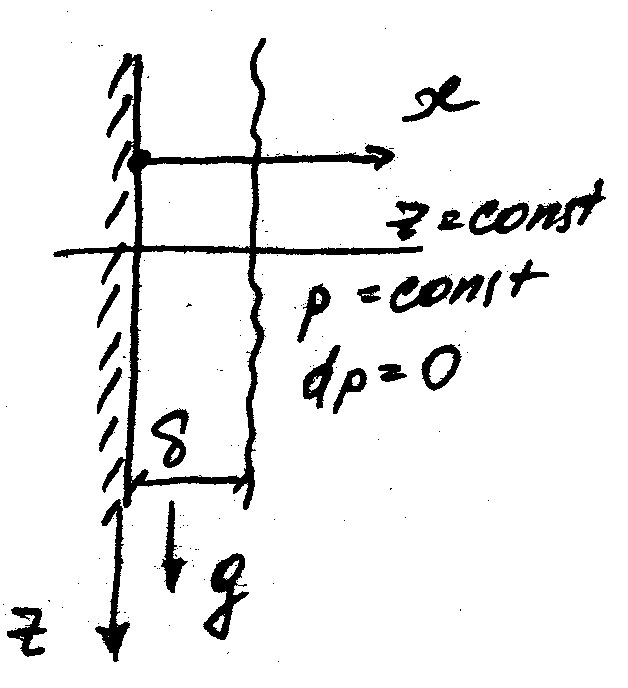
Z-![]()
![]() +ν(
+ν(![]() wz)=
wz)=![]() ;
;
1. движение под действием силы тяжести: Z=+g;
2. при
Z=const→dp=0→p= const:
![]()
![]() =0;
=0;
3. движение
стационарное:
![]() =0
=0
4. движение однонаправленное, т.е.
g
+ν![]() =0;
=0;
g
+![]() =0;
=0;
![]() =
=![]()
Интегрируем: Вводим граничные условия:
![]() =
=![]() х+С1;
х+С1;
![]() при
х=0;w=0
(явление прилипания)
при
х=0;w=0
(явление прилипания)
w=![]() х2+С1x+C2
при х=δ;
х2+С1x+C2
при х=δ;
![]() =0
=0
при х=0 и w=0 имеем С2=0
при
![]() =0
-
=0
-
![]() +С1
=0 →С1=
+С1
=0 →С1=![]()
Тогда распределение скорости по толщине пленки равно
w=![]() х2+
х2+![]() х
– параболическое распределение w
по толщине пленки
х
– параболическое распределение w
по толщине пленки
при х=0→ w=0
при х=δ→ wmax=![]() +
+![]() =
=![]()
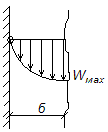
Средняя скорость движения пленки жидкости
Принимают dυ=wdf, где df=1м∙dx, т.е.расход на длине 1м
Тогда wср=![]() =
=![]() =
=![]()
![]() dx
dx
wср
=![]() [-
[-![]()
![]() ]=
]=![]() ;
;
wср=![]()
Отношение
![]() =
=![]()
Расход жидкости на длине 1м
υ
1=
δ wср
[![]() ]
– линейная плотность орошения
]
– линейная плотность орошения
υ
1=δ![]() ,
откуда δ=
,
откуда δ=![]()
Необходимо знать зависимость δ=f(Re).
Re=![]() =
=![]() ,
где dэкв=
,
где dэкв=![]() =
=![]() =4δср
=4δср
Re=![]() =
=![]() ,
откуда
,
откуда
υ 1=![]()
δ=![]() =
=![]()
δср=![]() справедливо приRe<20
(ламинарный режим)
справедливо приRe<20
(ламинарный режим)
δср=![]() 20<Re<1600
(волновой режим)
20<Re<1600
(волновой режим)
δср=0,185(![]() )
)![]() Re0,5
Re>1600
(турбулентный режим)
Re0,5
Re>1600
(турбулентный режим)
Изложенный метод применим для неньютоновских жидкостей. Так для дилатантных и псевдопластичных жидкостей
wср=![]()
![]()
![]()
δ=[![]()
![]() V1]
V1]![]()
Перемещение жидкостей (поршневые и ц/б насосы)
Напор и мощность насосов
|
|
1 метод определения напора
|
2 метод
Напор – разность удельных энергий на линии нагнетения и всасывания

Для пром. условий h=0
Мощность насоса
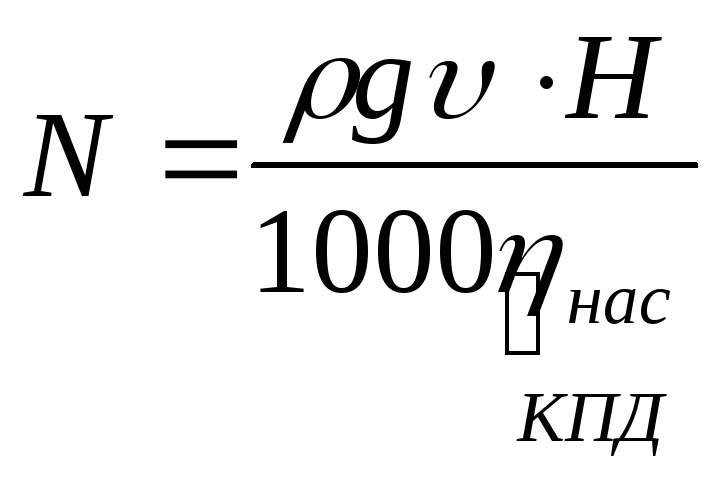 [кВт]
[кВт]
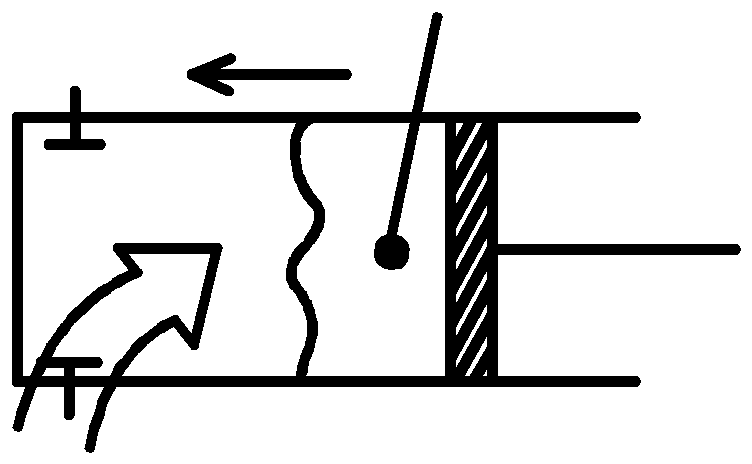
Поршневые насосы
-
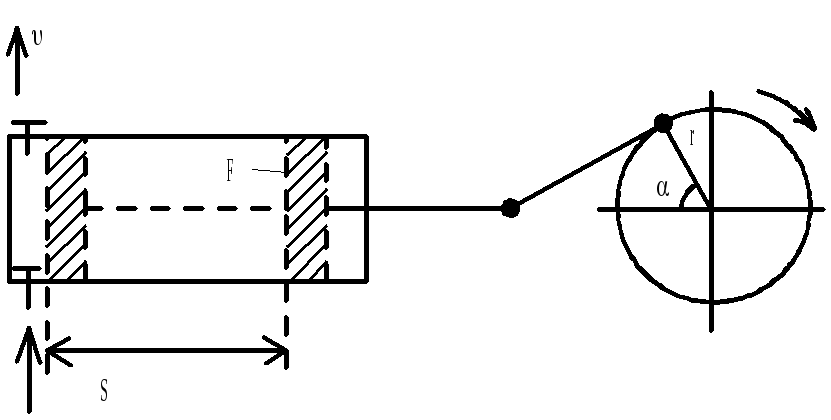
S – ход поршня
F – площадь поршня
FS – объём жидкости на 1 ход
![]()
![]() - для насоса однократного действия
- для насоса однократного действия
Насос двойного действия
Насос тройного действия – 3 насоса одинарного действия
-
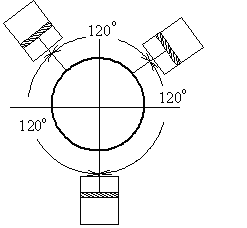
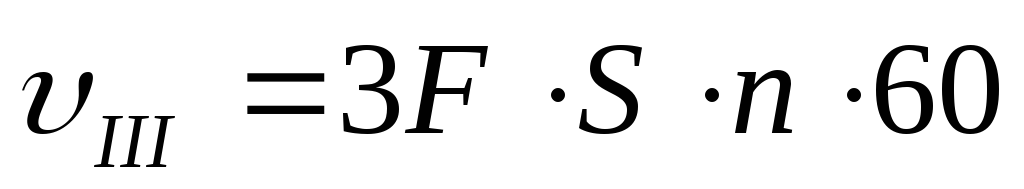
 - 2 насоса двойного действия
- 2 насоса двойного действия
![]()
![]() - кратность действия
- кратность действия
![]()
![]() <1
за счёт плохой работы клап. короб.
<1
за счёт плохой работы клап. короб.
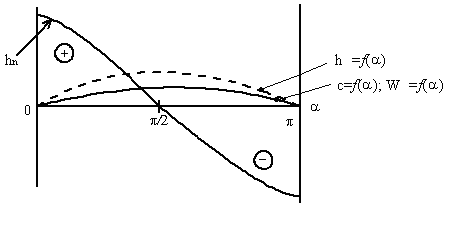
Зависимость производительности от хода поршня
Закон хода поршня
![]()
![]() - радиус кривошипношатунного механизма
- радиус кривошипношатунного механизма
![]()
С – скорость поршня
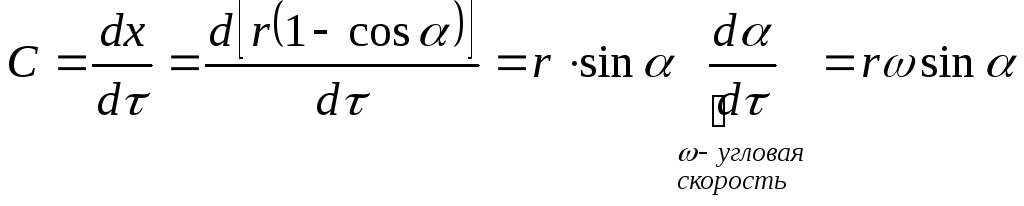
![]() ;
;
![]() ;
;
![]() ;
C=0
;
C=0
![]() ;
;
![]() ;
;
![]() ;
C=max
;
C=max
Производительность
![]()
-
i=1
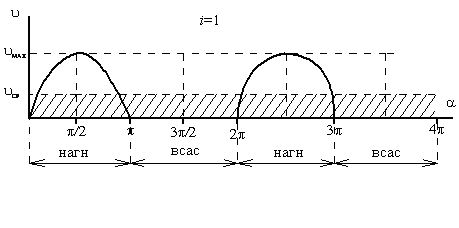
Диаграмма подачи
(производительности)
поршневых насосов
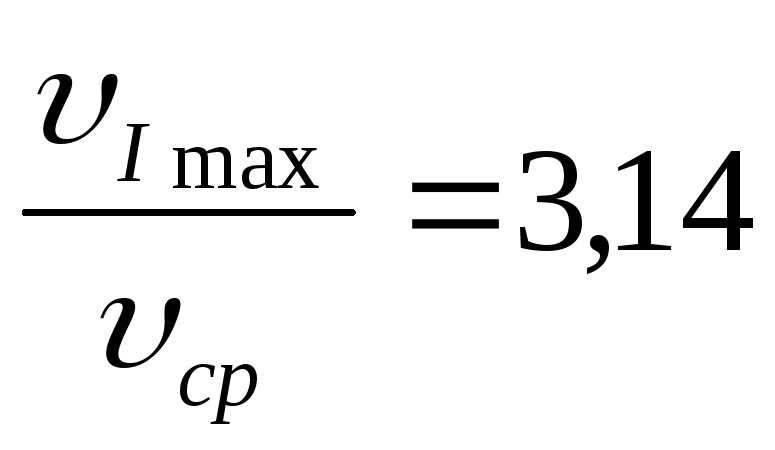
i=2
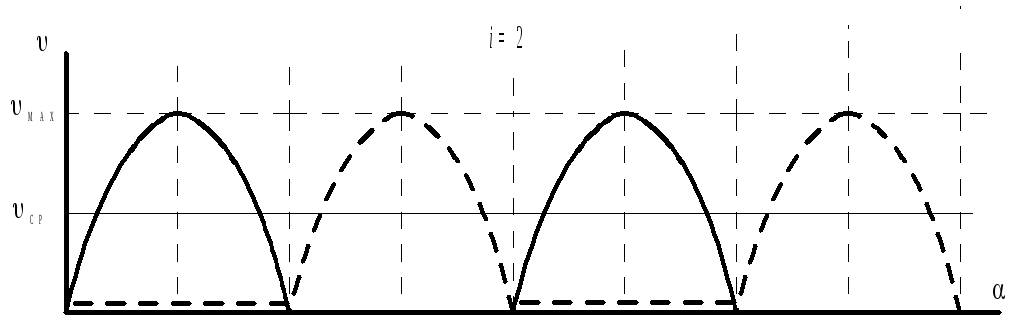
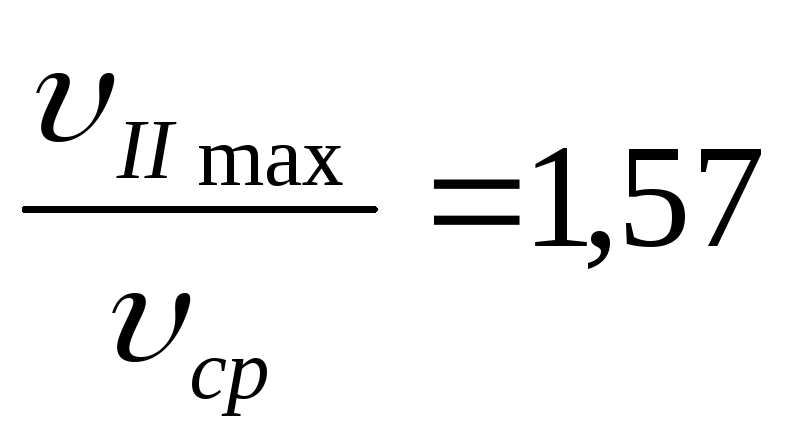

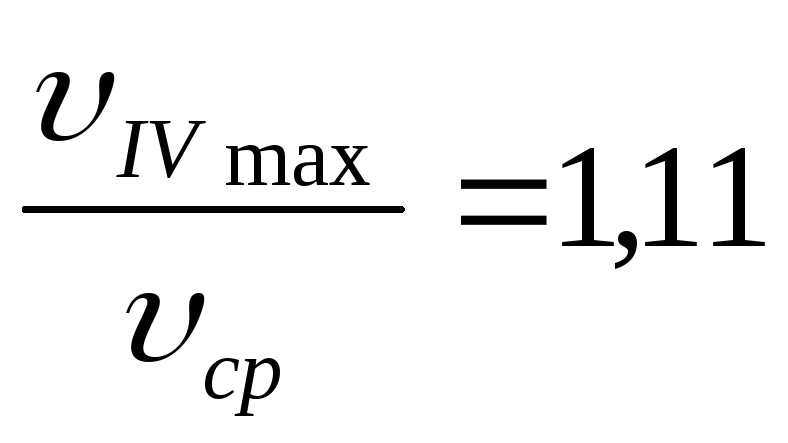
Недостаток поршневого насоса -
неравномерность подачи геометрическая
высота всасыв. поршневого насоса.
Движущей силой процесса всасыв. явл.
![]() ,
которая расходуется
,
которая расходуется
подъем жидкости н-а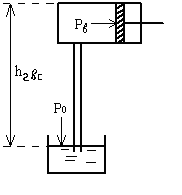

преодолеть гидр. сопр.
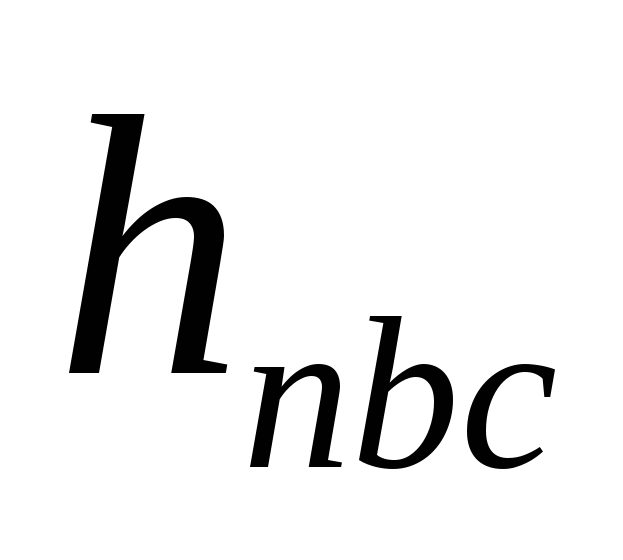
инерционные потери

![]()
![]()
|
|
Гидравлический удар
|
|
![]() -
парциальное давление паров перекачив.
жидкости при т-ре T
-
парциальное давление паров перекачив.
жидкости при т-ре T
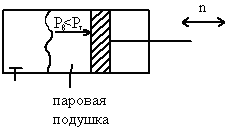
В цикле нагнетания вакуум
|
|
![]()
![]()
![]()
![]() -
конденсация паровой подушки
-
конденсация паровой подушки
![]() резкоеV
резкоеV![]()
![]() ;
t- справочник
;
t- справочник
![]() гидравлический удар. Определение
инерционных потерь во всасыв.????
гидравлический удар. Определение
инерционных потерь во всасыв.????
Сила инерции массы жидкости во всасыв. тр-де.
![]() - закон Ньютона
- закон Ньютона

![]() a- ускорение
a- ускорение
m
На преодоление этой силы инерции расход. часть напора насоса
![]()
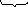
![]()
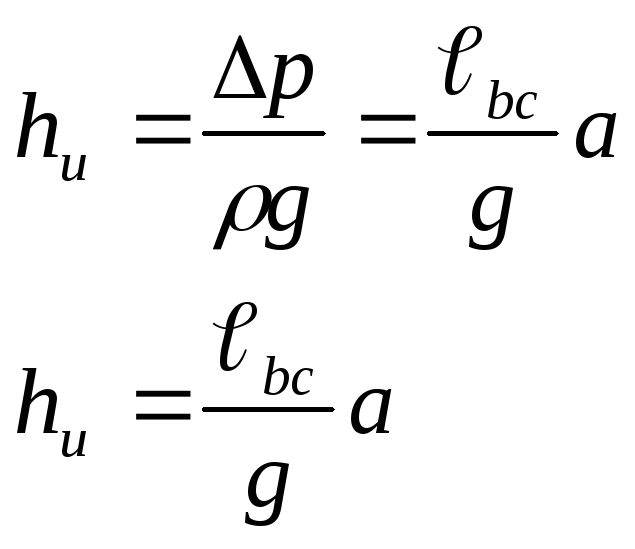
![]()
![]()
ускорение массы жидкости в трубопроводе
Используем ур-е неразрывности
![]()
![]()
![]()
![]()
![]()
площадь всасыв. ускорение поршня
тр-да
![]()

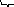
w
|
|
 Сопоставим
гидр. и инерционные потери во всасыв.
тр-де
Сопоставим
гидр. и инерционные потери во всасыв.
тр-де
|
|
![]() ~
~
![]() ~
~![]()
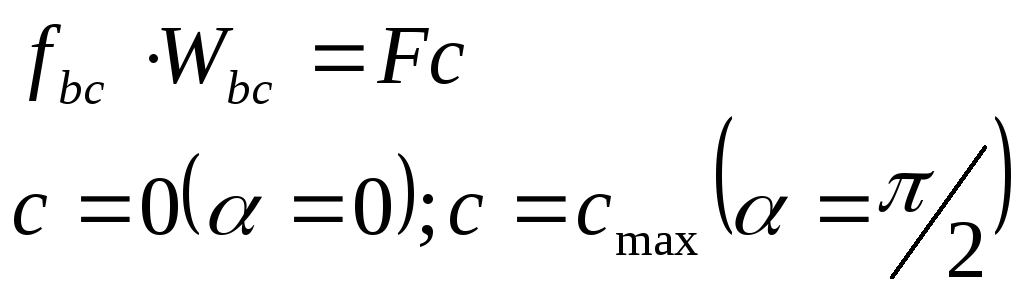
![]() ~
~
![]()
![]()
![]()
![]()
![]()
10м
![]()
Центробежные насосы, за счет передачи ж-ии ц/б передаем создаем напор
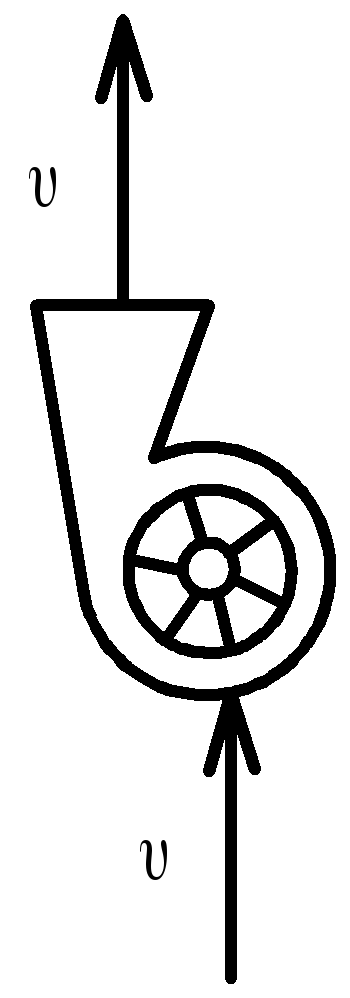
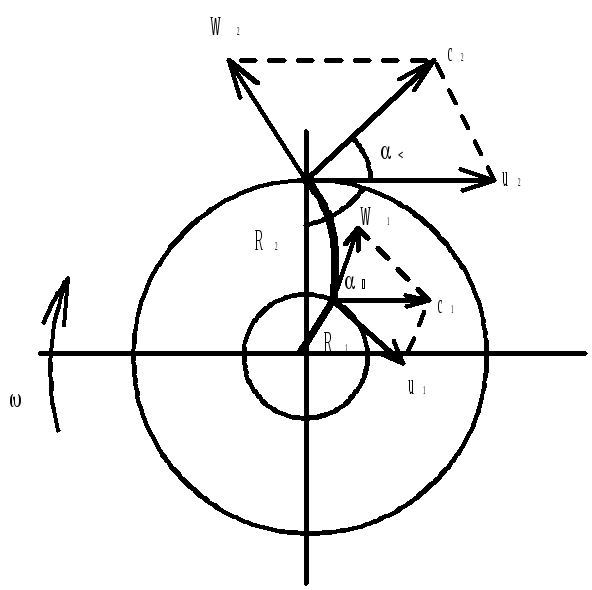
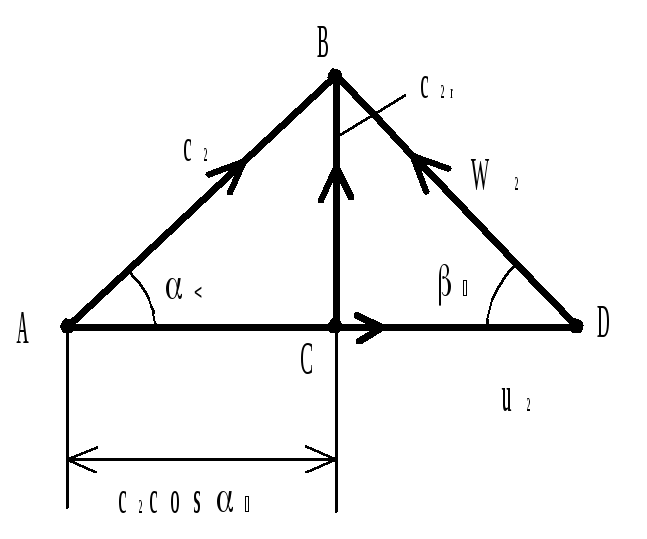
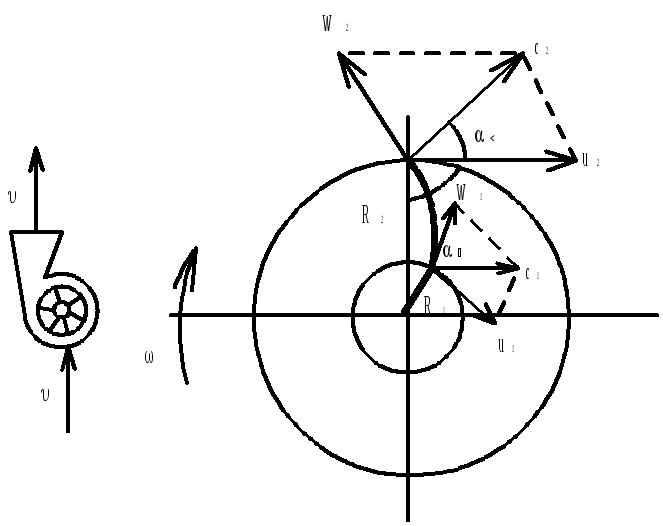
Вывод основного ур-я ц/б насоса
|
|
W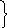 -
относительная скорость
-
относительная скорость
u- окружная скорость на выходе 2
c- абсолютная скорость на входе 1
Сумма кол-ва движения равна моменту равнодейств.
сил (для 1 элемент. частицы)
![]() -
плечо на выходе
-
плечо на выходе
Момент на выходе
![]() -
сумм. момент
-
сумм. момент
Домножим на w правую и левую части
![]() -
мощность насоса
-
мощность насоса
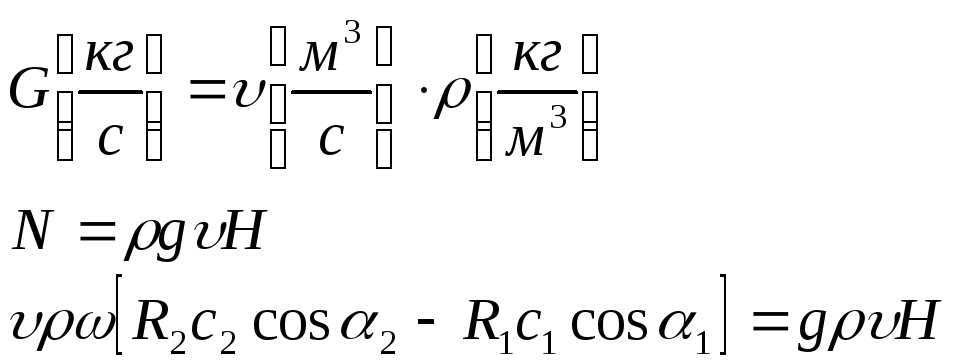
![]() -
окружная скорость
-
окружная скорость
|
|
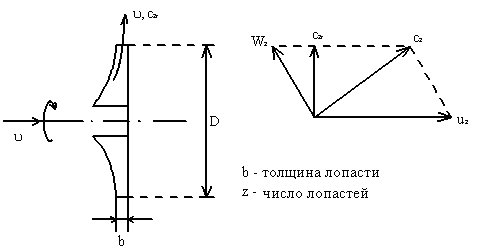
Для безудержного входа жидкости на рабочее колесо,
![]() (конструктивно)
(конструктивно)
![]()
![]()
За счет некоторого неподобия
![]() скоростей на входе и выходе лопатки
появл. объемный кпд.
скоростей на входе и выходе лопатки
появл. объемный кпд.
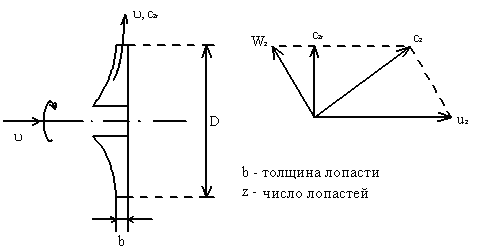
Производительность ц/б насоса
|
|
|
![]()
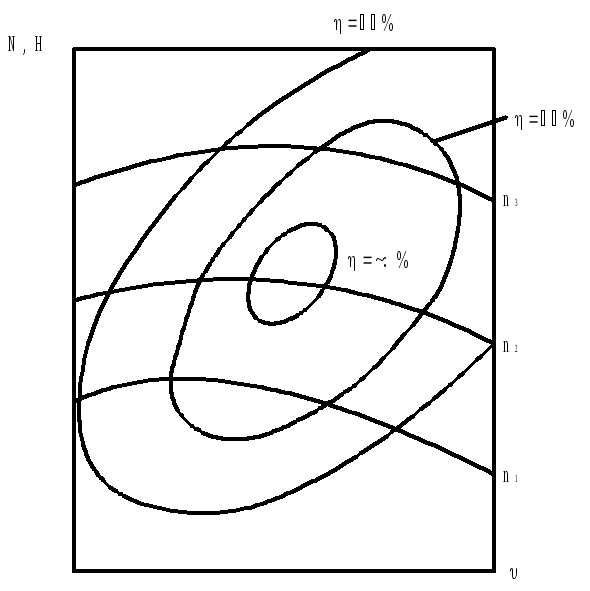
![]() Зависимость
напора от производительности
Зависимость
напора от производительности
|
|
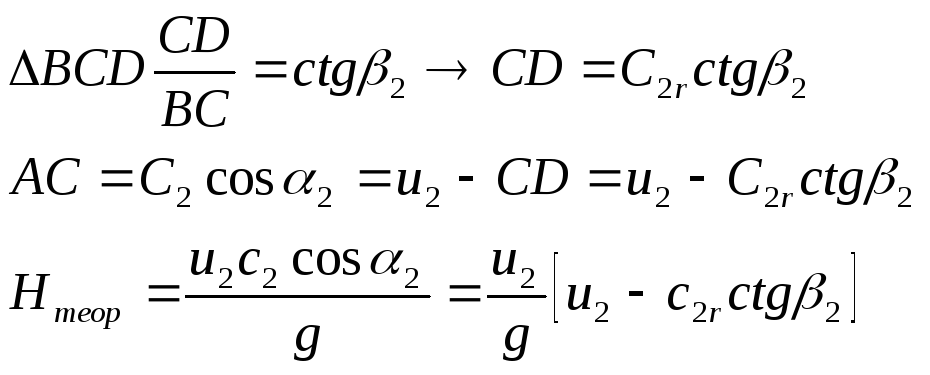
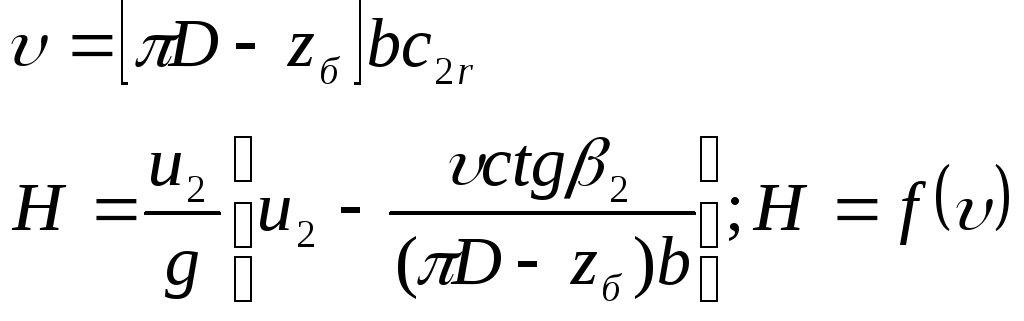
|
|
|
|
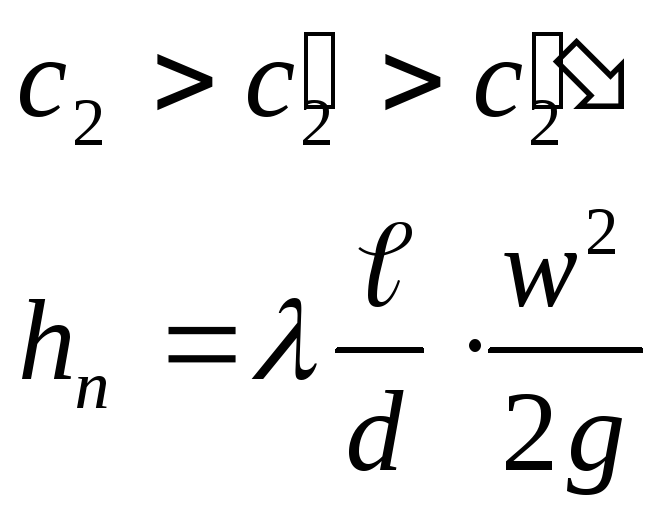
чем больше
![]()
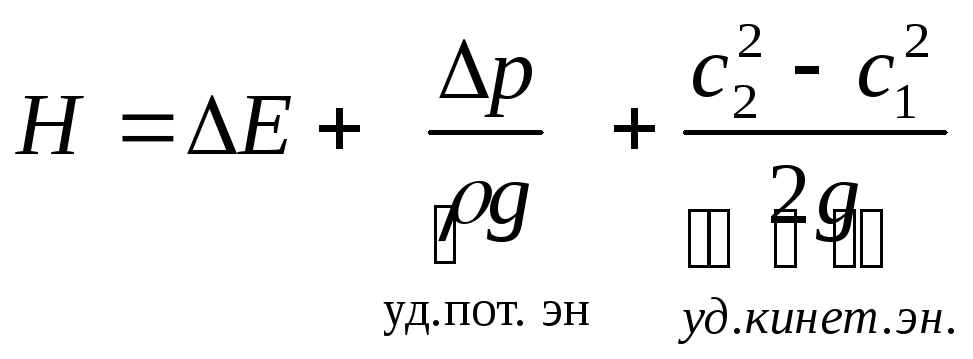
![]()
пренебрегаем
Действительная зависимость напора от производительности
|
|
Кавитация в ц/б насосе.
при
![]() -
жидкость закипела
-
жидкость закипела
при
![]() -
конденсация, микровакуум
-
конденсация, микровакуум
струйка Ж бьет в обл-ть вакуума
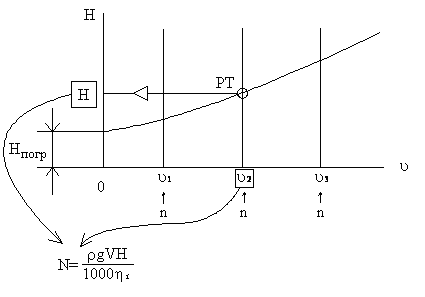
Рабочая точка ц/б насоса
![]()
|
|
Геометрическая высота всасывания
-
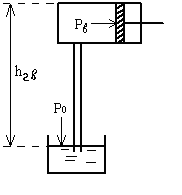
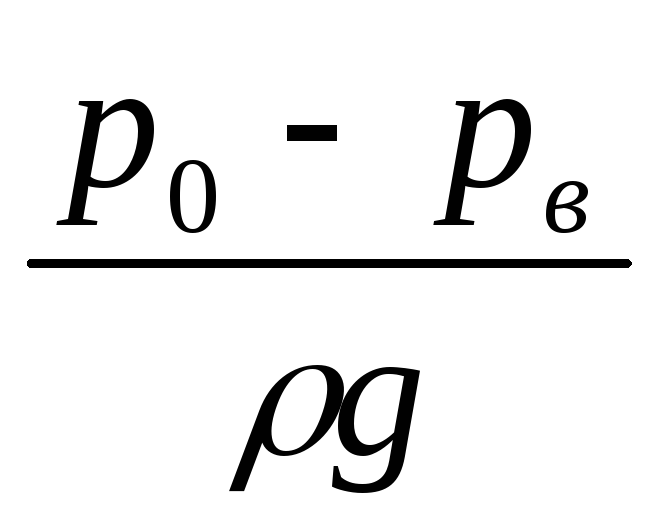 - движущая сила подъёма жидкости на
высоту
- движущая сила подъёма жидкости на
высоту
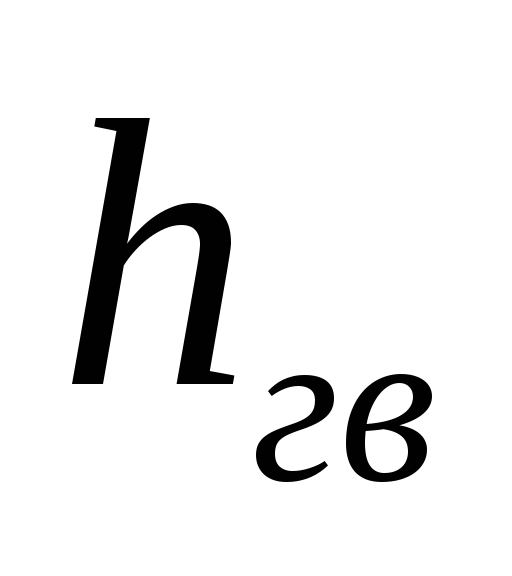
Она расходуется:
- на подъём жидкости на высоту
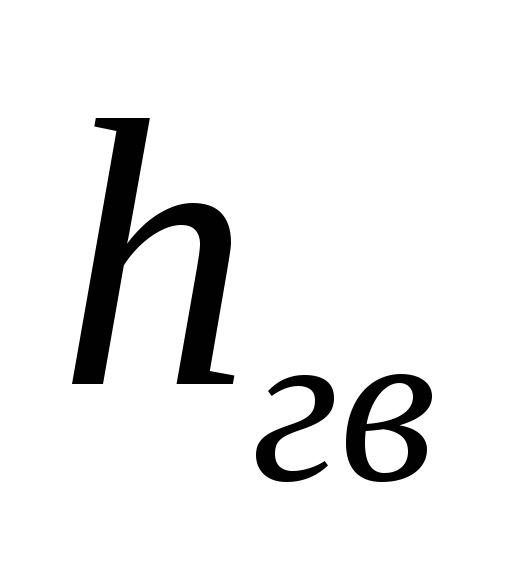
- на преодоление гидравлического сопротивления всасыв. т/п (
 )
)- на преодоление инерционных потерь (
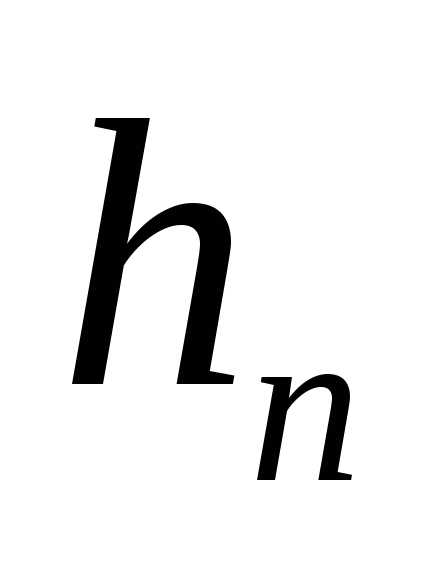 )
)таким образом
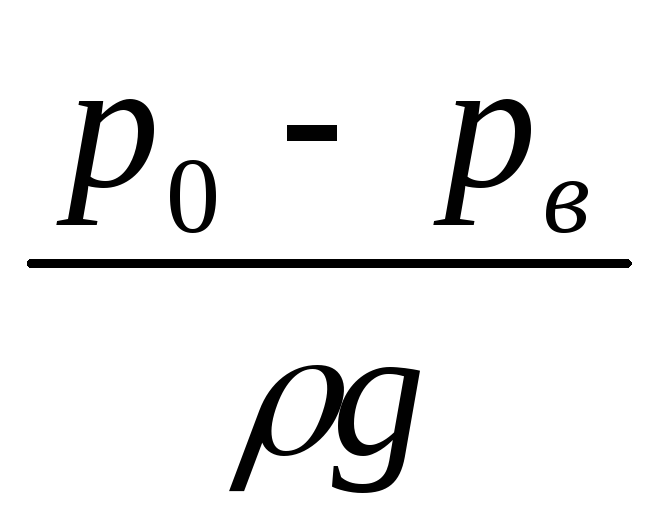 =
= +
+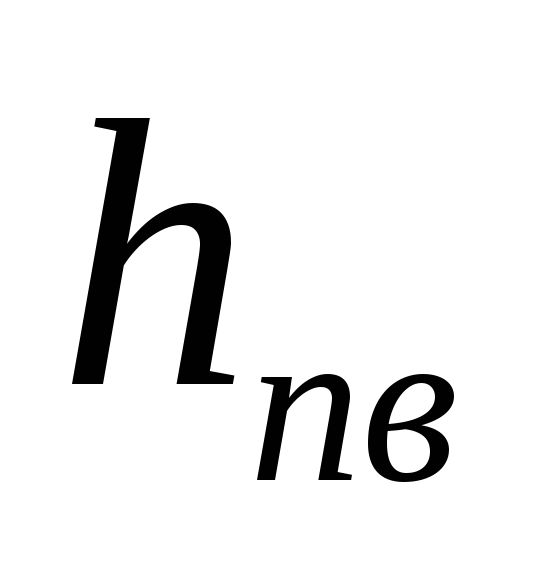 +
+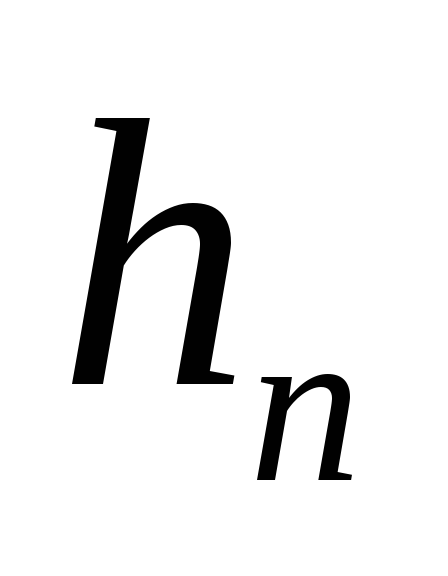 ,
откуда
,
откуда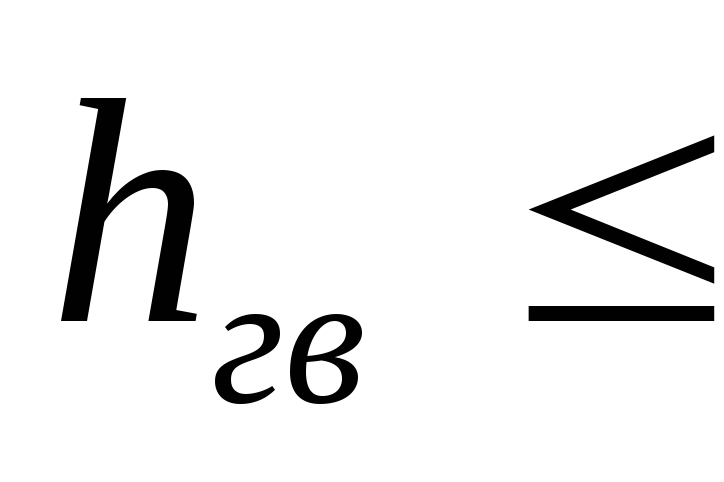
 -
-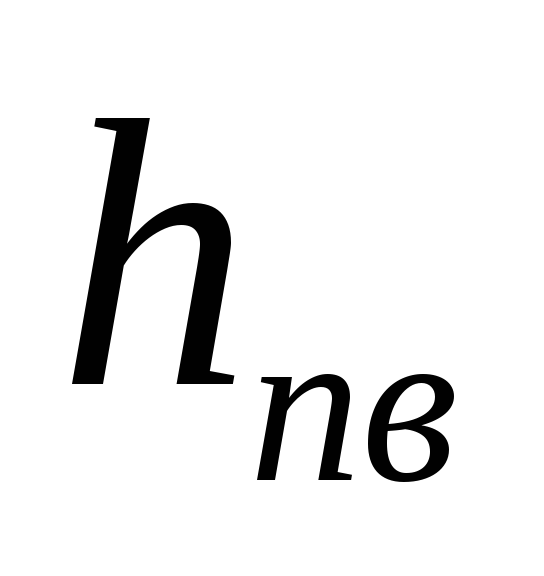 -
-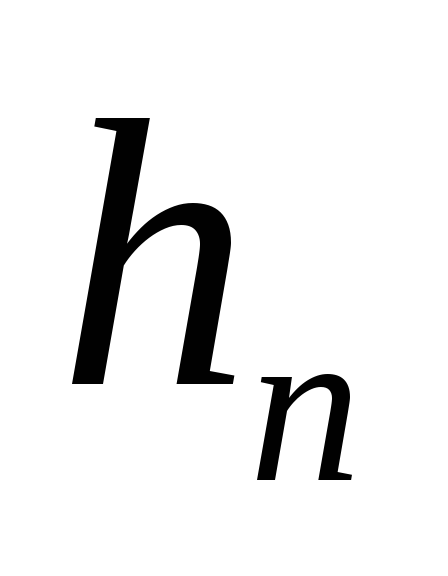
![]() - определяется (лимитируется) условиями
гидравлического удара
- определяется (лимитируется) условиями
гидравлического удара
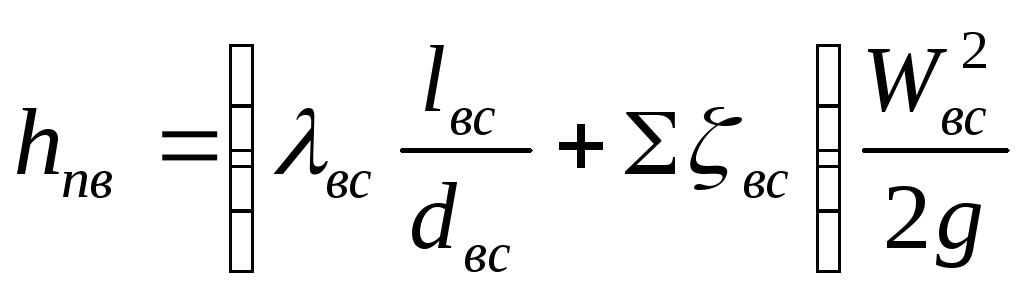
![]() =?
Сила инерции массы жидкости во
всасывающем т/п
=?
Сила инерции массы жидкости во
всасывающем т/п

На преодоление этой силы тратится часть силы давления:
![]()
тогда
![]()
Представим это
![]() через
через![]() :
:
![]()
Напишем уравнение неразрывности:
![]() или
или
![]() ,
где
,
где

таким образом,
![]()
поэтому
![]()
В итоге
Сравним
![]() и
и
![]()
|
|
Дать объяснение воздушному колпаку
Без воздушного колпака
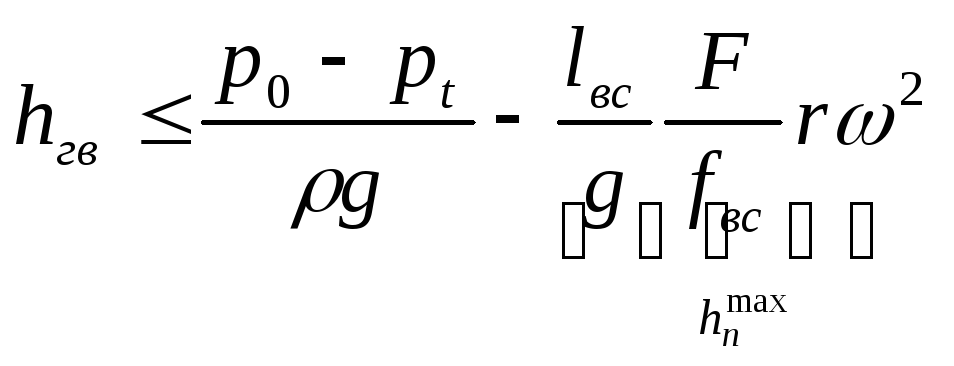 возможно, что
возможно, что
![]() !
!
С воздушным колпаком

Рабочая точка поршневого насоса
|
|
|
|
|
|
| |||
Центробежные насосы
Вывод основного уравнения ц/б насоса
|
|
W – относительная скорость u – окружная скорость с – абсолютная скорость Сумма количества движения равна моменту равнодействующих сил
|
Но
![]() ;
;
![]()
![]() ;
;
![]() и
и
![]() тогда
тогда
Основное уравнение ц/б насоса
|
|
Конструктивно делают “безударный”
выход, т.е.
![]()
![]() и
и
![]()
Производительность ц/б насоса
|
|
|
Зависимость напора H
от производительности
![]()
|
|
Из
тогда:
|
![]() ,
но
,
но
![]()
|
|
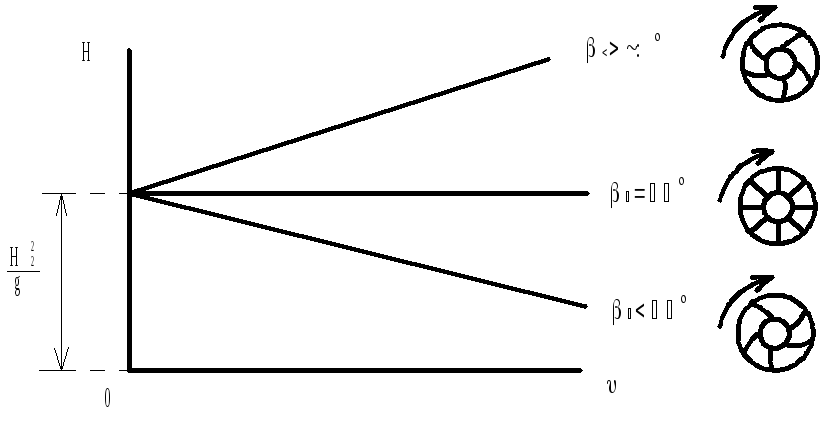
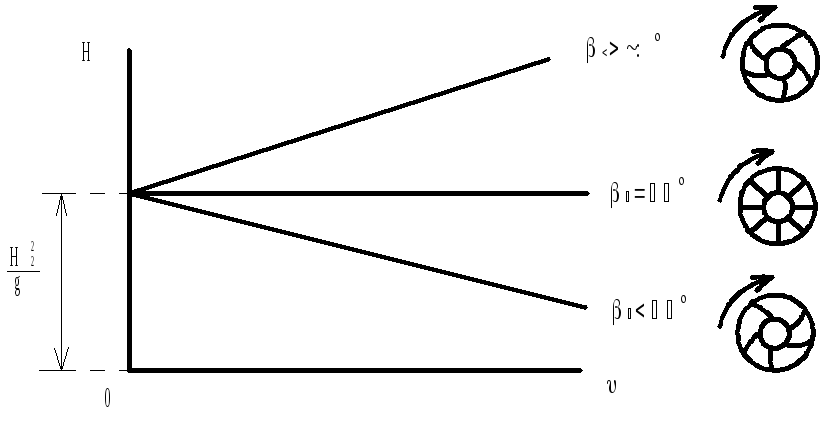
Анализ уравнения
![]()
При
![]() :
:
![]()
|
|
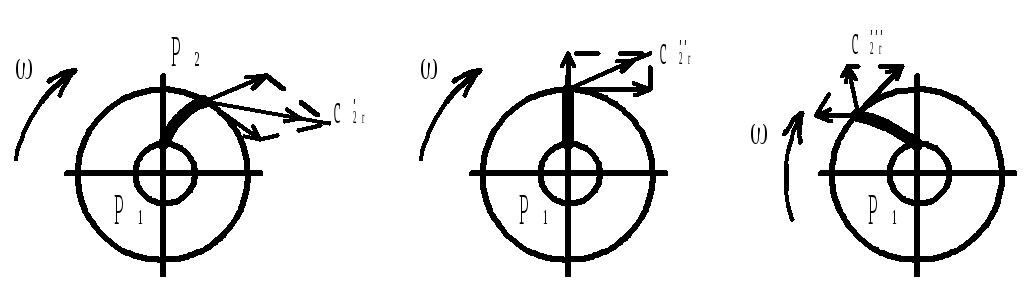
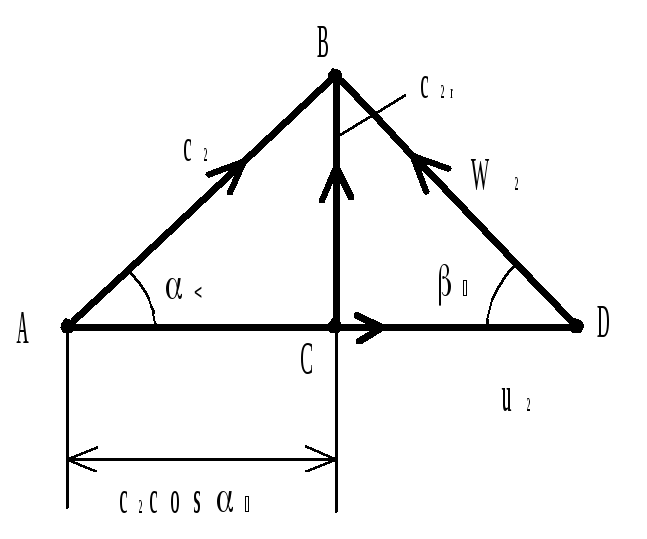
Выбор профиля лопаток рабочего колеса
|
| ||
|
25% потенциальная энергия 75% кинетическая энергия |
|
25% кинетическая энергия 75% потенциальная энергия |
![]()
![]() мало из-зи
мало из-зи
![]()
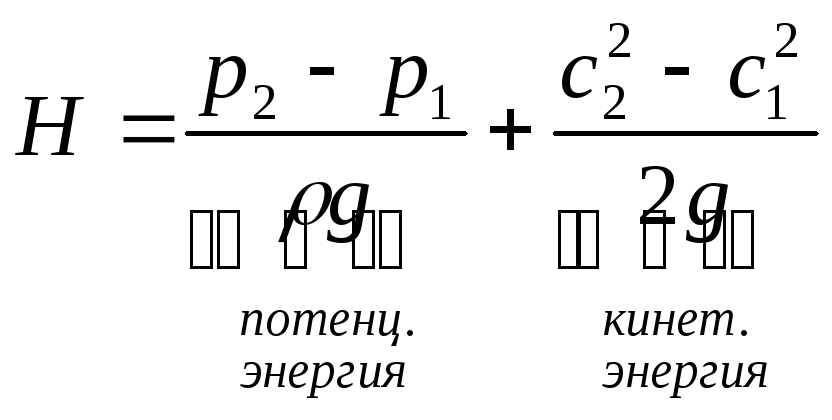
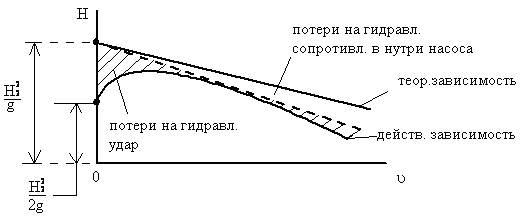
Действительная зависимость
![]()
|
|
Явление кавитации
Поэтому
![]() ,
,
Где
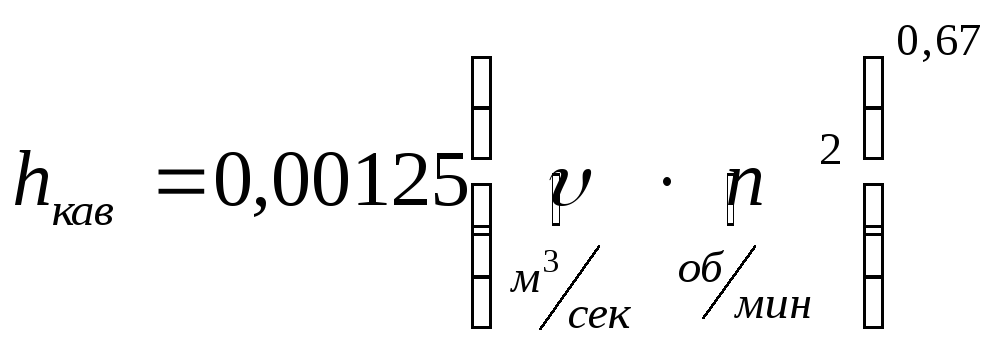
Частные и общая характеристики ц/б насоса
![]() - частные характеристики
- частные характеристики
|
|
Рабочая точка центробежного насоса
|
Гидравлика дисперсных систем
Осаждение представляет собой процесс разделения фаз под действием силы тяжести, сил инерции или электростатических сил.
Рассмотрим силы,
действующие на одиночную частицу в
сплошной среде (плотность
миделево сечение G
Частица движется равномерно и прямолинейно под действием силы тяжести G
На частицу
действует выталкивающая архимедова
сила А и ее движению препятствует сила
гидравлического сопротивления
Баланс сил: G=А
+
G=
А=
hп=
основное критериальное уравнение процессов осаждения.
Коэффициент сопротивления определяется в зависимости от режима осаждения.
турбулентный Ламинарный Lg Re
2 500(800)
Ламинарный режим
Re
Турбулентный
режим Re
Переходный режим
Определение скорости падения частицы
Ламинарный режим
Ar =18 Re ;
Формула применима для ламинарного режима в условиях не стесненного осаждения (концентрация твердой фазы не превышает 5% объемных).
|
|
Осаждение в поле сил тяжести (отстаивание)
Отстойник периодического действия
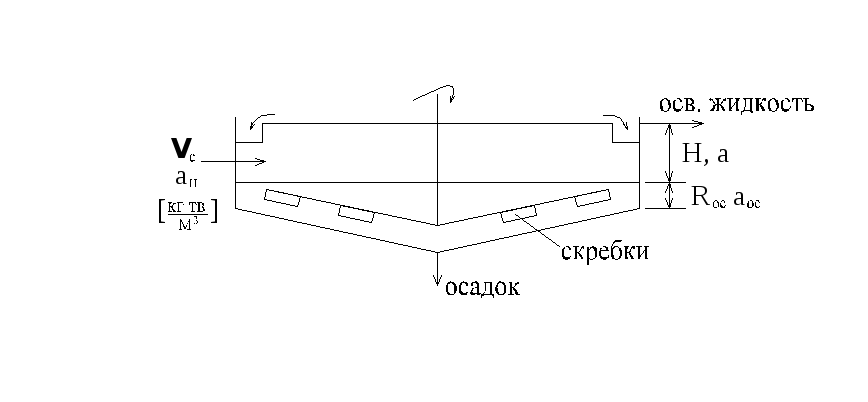
![]() к
к![]() -концентрация
твердой фазы
-концентрация
твердой фазы
Составляем материальный баланс по твердой фазе:
![]() ,
,
причем
![]()
![]() ;
;
![]() ;
;
![]() ,
,
откуда
![]()
![]() =
=![]()
![]()
![]()
Но
![]() ,
,
где
![]() -
скорость стесненного осаждения;
-
скорость стесненного осаждения;![]()
Производительность отстойника
Vотс(![]() )=
)=![]()
![]()
Производительность отстойника зависит от F, но не от высоты
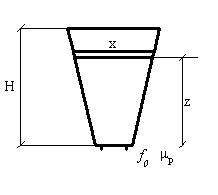
Отстойник полунепрерывного действия

Пути
![]() иН
частицы должны проходить за одно и то
же время, поэтому
иН
частицы должны проходить за одно и то
же время, поэтому
![]() ,
откуда
,
откуда
![]()
-производительность
отстойника; ![]() -объем
отстойника
-объем
отстойника
![]() =
=![]()
Vотс=b![]()
![]() )
)
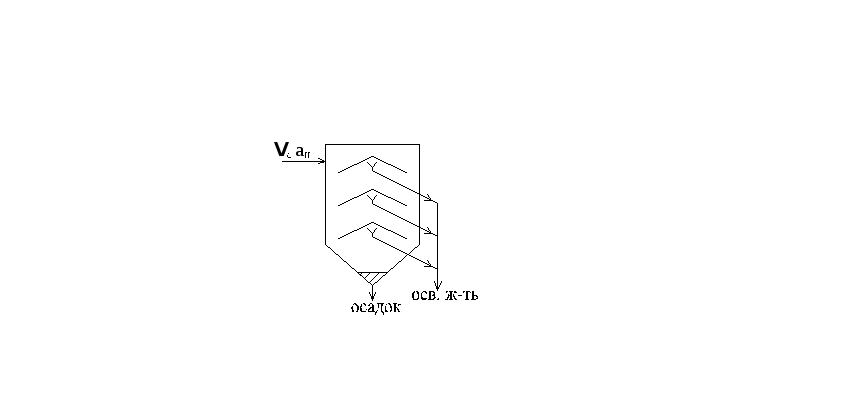
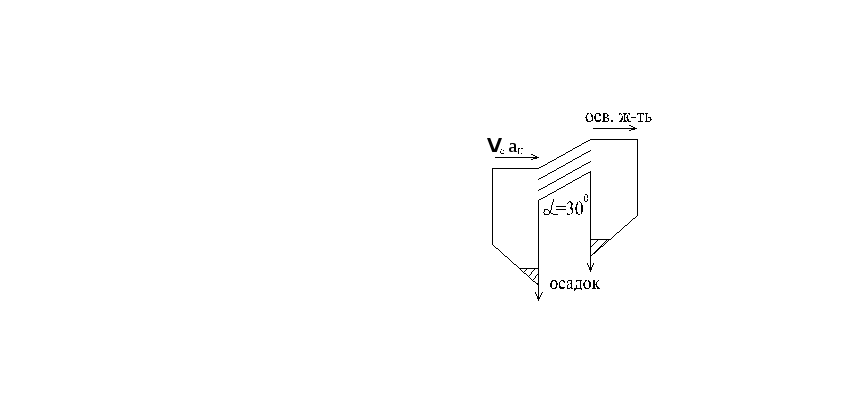
Некоторые конструкции отстойников непрерывного действия
колонный отстойник полочный отстойник



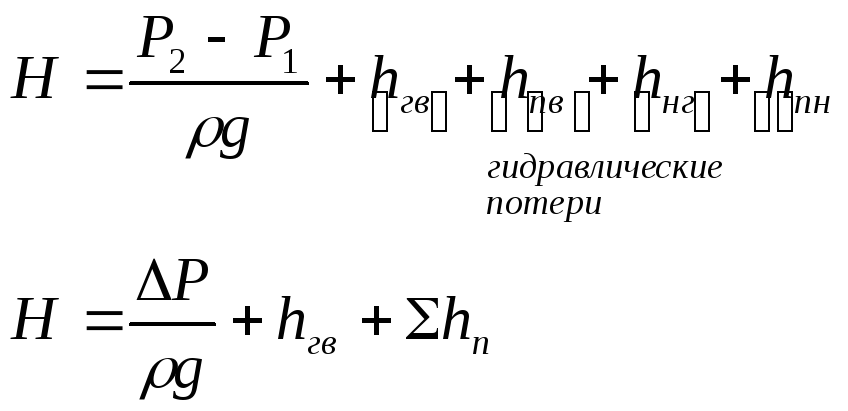



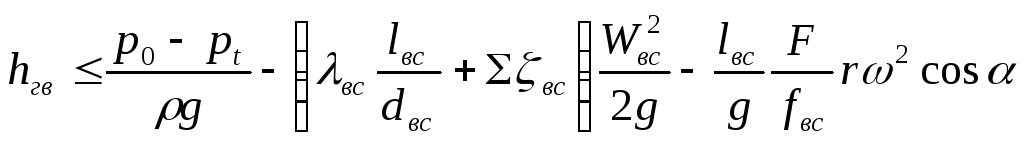
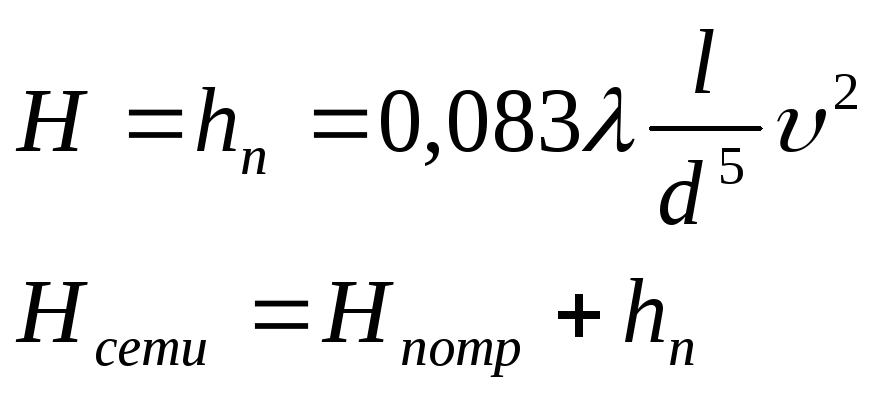







 Rг
Rг

 p
p



 Lg
Lg