4.3.4 Нулевой метод

Этот метод является развитием дифференциального метода. В отличие от последнего результирующий эффект от одновременного воздействия измеряемой величины и величины, воспроизводимой мерой на устройство сравнения (компаратора) доводят до нуля. В этом случае за счет применения высокочувствительного нуль-индикатора повышается точность измерения по сравнению с дифференциальным методом, поскольку выражение для погрешности (4.19) практически трансформируется в выражение

.

Нулевым методом измеряют сопротивления резисторов, емкости конденсаторов, индуктивности катушек с помощью одинарных и двойных мостов постоянного и переменного тока.

Перечисленные методы могут встречаться на практике как непосредственно, так и в виде их модификаций. В различных сочетаниях эти методы лежат в основе функционирования современных СИТ, позволяющих производить автоматическую коррекцию погрешности.

4.4 Обобщенные структурные схемы сит

Современные СИТ состоят из совокупности ИУ и СИ, соединенных в различных сочетаниях с целью реализации того или иного метода измерения. Соединение этих звеньев в определенную цепь преобразований носит название структурной схемы. Структурные схемы очень разнообразны. Однако все они соответствуют двум основным видам структурных схем: прямого и уравновешивающего преобразования.

4.4.1 Схема прямого преобразования

По этой схеме построены многие СИТ. Отличительная особенность этой схемы состоит в том, что преобразование измерительного сигнала производится в прямом направлении (рис. 4.5).

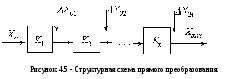
Если коэффициенты преобразования отдельных звеньев равны , то общий коэффициент преобразования будет равен

(4.20)

и уравнение всего измерительного преобразования имеет вид

. (4.21)

На работу измерительного прибора будут оказывать влияние нестабильность коэффициентов преобразования , а также дрейф нуля, помехи и наводки.

Оценим влияние этих погрешностей на результирующую погрешность СИТ.

Абсолютная погрешность измерения выходной величины , обусловленная нестабильностью коэффициентов преобразования, может быть получена суммированием частных производных выражения (4.21), умноженных на соответствующие нестабильности

.

Отсюда можно найти относительную погрешность преобразования

,

т.е. результирующая погрешность равна сумме относительных погрешностей преобразования.

Оценим теперь погрешность, обусловленную дрейфом нуля и наводками. Очевидно, она будет равна

,

таким образом, погрешность, вносимая первым преобразователем, умножается на все последующие коэффициенты преобразования. Поэтому именно к первичному преобразователю при проектировании СИТ предъявляются наиболее жесткие требования по точности и стабильности. Для достижения высокой стабильности всего СИТ требуется высокая стабильность всех входящих в него звеньев.

4.4.2 Структурная схема уравновешенного преобразования

Особенность схемы (рис. 4.6) состоит в том, что выходная величина подвергается обратному преобразованию в величину, однородную с входной величинойи почти полностью уравновешивает её, в результате чего на вход цепи прямого преобразования поступает только небольшая частьпреобразуемой величины. Другими словами, используется отрицательная обратная связь.

Возможны два режима работы схемы: режим неполного уравновешивания и режим полного уравновешивания.

1.Режим неполного уравновешивания.

В этом режиме входная и уравновешивающаявеличины образуют разность.

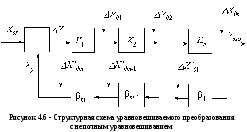
Уравнение цепей прямого и обратного преобразования будут иметь вид, соответственно и, где. Отсюда имеем

. (4.22)

Производя перегруппировку, получаем или

. (4.23)

Коэффициент преобразования уравновешивающего СИ будет равен

. (4.24)

При , т.е. цепь прямого преобразования слабо влияет на работу прибора, однако его чувствительность падает в (1+K) раз.

Определим относительную погрешность, обусловленную нестабильностью коэффициентов преобразования идля этой схемы. Для этого продифференцируем выражение (4.23) пои

(4.25)

и деля его на , получаем

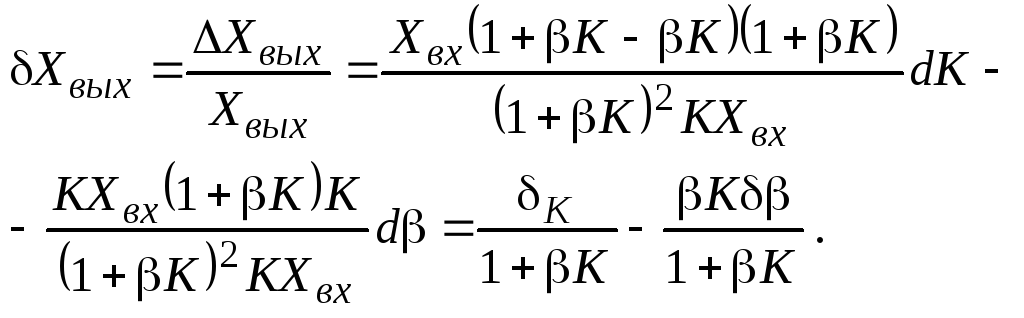(4.26)

Таким образом, относительная погрешность состоит из суммы двух членов, один из которых пропорционален суммарной погрешности всех преобразователей цепи прямого преобразования, а другой – суммарной погрешности преобразования цепи обратной связи. Причем погрешность от нестабильности цепи уменьшается враз, а погрешность, обусловленная нестабильностью цепи обратной связи, почти полностью входит в суммарную погрешность. Действительно, при. Следовательно, в прямой цепи можно использовать нестабильные преобразователи, необходимо только, чтобыи коэффициент обратного преобразования имел высокую стабильность. Необходимо учитывать, что введением обратного преобразования враз уменьшается чувствительность измерительного устройства. Для её сохранения коэффициентнужно увеличить враз. При этом могут возникнуть условия для самовозбуждения СИТ. Поэтому предел увеличенияопределяется динамической устойчивостью прибора.

Необходимо отметить, что нелинейность функции прямого преобразования можно рассматривать как изменение коэффициента преобразования относительно номинального значения.

Это изменение может быть вызвано и другими причинами: вариацией параметров окружающей среды (температуры, давления, влажности), инерционностью звеньев, механическими воздействиями (вибрацией, тряской) и т.п. Введение обратного преобразования одинаково уменьшает влияние всех вышеперечисленных причин.

Оценим погрешность, обусловленную дрейфом нуля, наводками и т.п. Для этого введем в схему дополнительные сигналы . Приводя эти сигналы к входу схемы, получаем

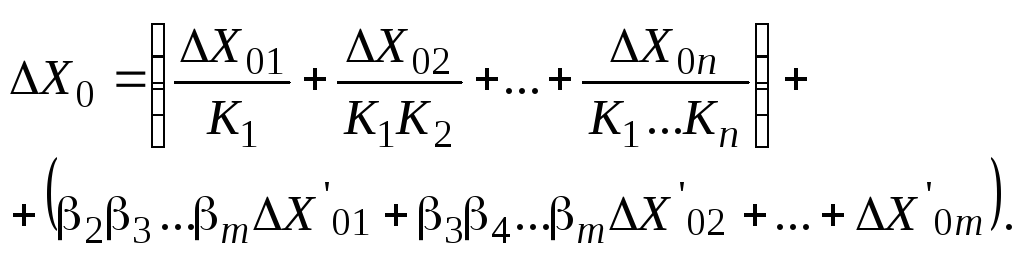(4.27)

Из этого выражения видно, что аддитивная погрешность не зависит от глубины обратной связи и не может быть уменьшена по абсолютной величине введением схемы уравновешивающего преобразования.

Наибольшее требование по минимальному дрейфу нуля предъявляется к первому прямому и первому обратному преобразователю.