3. Система збіжНихСил

3.1. Приведення до рівнодійної. Правило многокутника сил

Найпростішою є система збіжних сил, тобто система сил, лінії дії яких перетинаються в одній точці (точці О збігу сил). Вона може бути просторовою чи плоскою. В останньому випадку всі лінії дії сил системи належать одній площині.

Теорема про рівновагу. Система збіжних сил еквівалентна одній силі (рівнодійній), яка дорівнює геометричній (векторній) сумі цих силі прикладена в точціО їх збігу.

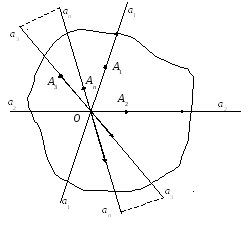
Доведення. Розглянемо (рис. 3.1,а) вихідну систему збіжних сил з лініями діїі точками прикладання.

Для кожної сили системи використовуємо аксіому 2 про перенесення сили уздовж лінії дії в точку О збігу (рис. 3.1,б). У результаті отримаємо систему сил , прикладених в одній точціО.

На основі аксіоми 3 про паралелограм сил будь-яку кількість сил із загальною точкою прикладання можна складати геометрично. При цьому можна використовувати або правило паралелограма, або правило трикутника (многокутника).

У першому випадку (рис. 3.1,б), застосовуючи послідовно правило паралелограма, дістанемо спочатку рівнодійну , далі отримаємо рівнодійнуі нарешті рівнодійнузаданої системи сил (рис. 3.1,б).

За правилом многокутника рівнодійну сил (рис. 3.1,в) визначаємо як суму векторів цих сил: для цього з кінця вектора відкладаємо вектор сили, і т.д. З’єднавши початок першого вектораз кінцем останнього, визначимо рівнодійну силу

а)

О

в)

б)

Рис. 3.1

.

Одержаний таким чином многокутник має назву многокутника сил, або силового многокутника, замикальна сторона якого виявляється рівнодійною силою системи.

Таким чином, теорему доведено.

Доведена теорема дозволяє розв’язувати задачу приведення систем збіжних сил до рівнодійної сили графічно (нею зручно користуватись у разі плоскої довільної системи сил).

Рівнодійну можна визначити також аналітично за її проекціямина осі прямокутної системи координат методами векторної алгебри. У даному випадку рівнодійнупредставляють так:

, (3.1)

де ; ; ; - проекції сил системи на відповідні осі координат; - координатні складові рівнодійної.

Величина (модуль) і напрямні косинуси рівнодійної сили визначають, враховуючи (3.1), за наступними формулами:

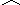
; (3.2)

;;.

Визначивши проекції або величину і напрямні косинуси рівнодійної, можна побудувати і сам вектор у заданій системі координат для подальшого розв’язання задачі рівноваги тіла.

Розглянемо, наприклад, задану в площині хОу (рис. 3.2,а) систему двох збіжних сил Н,Н. Визначимо рівнодійнусистеми методом

а б

Рис. 3.2

додавання векторів початкових сил за правилом паралелограма, а також методом додавання координатних складових рівнодійної за правилом прямокутника (плоска система сил) або паралелепіпеда (просторова система) чи за правилом “модуль-кут”.

У першому випадку будуємо на силах , як на сторонах, паралелограм (рис. 3.2,а), діагональ якого буде шуканою рівнодійною. Величину (модуль) рівнодійної визначаємо за теоремою косинусів:

(Н).

У другому випадку отримаємо: проекції рівнодійної

(Н),

(Н),

координатні складові рівнодійної:

.

Вектори ібудуємо на рис. 3.2,б. Склавши їх за правилом прямокутника, отримаємо шукану рівнодійну.

За правилом “модуль-кут” визначаємо величину рівнодійної

(Н), її напрямний косинус

і кут . Будуємо в площиніхОу лінію дії а-а рівнодійної (рис. 3.2,б), враховуючи визначений кут між нею і віссю Ох. Далі на лінії дії а-а будуємо вектор рівнодійної, який починається в полюсі О системи координат і має величину (довжину) (Н).