
3. Метод виділення цілої частини
Цей метод передбачає додавання( і одночасно віднімання) до чисельника підінтегральної функції такого виразу, що при наступному почленному діленні з’явилася ціла частина
Покажемо як це робиться на прикладах. Першим прикладом розберемо табличний інтеграл №14, який ми фактично вирішили цим методом
Приклад
1 ∫ =∫
=∫ =
домножимо
чисельник та знаменник на 2a
=
=
домножимо
чисельник та знаменник на 2a
= ∫
∫ dx=
потім
до чисельника додаємо x
і
віднімемо x
а
далі поділимо почленно =
dx=
потім
до чисельника додаємо x
і
віднімемо x
а
далі поділимо почленно = ∫
∫ dx=
dx=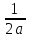 ∫
∫ dx=
dx= ∫
∫ dx-
dx-
- ∫
∫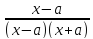 dx=
dx= ∫
∫ -
- ∫
∫ =
= ln|x-a|-
ln|x-a|- ln|x+a|+c=
ln|x+a|+c= ln|
ln| |+c.
Ми отримали потрібний нам результат.
|+c.
Ми отримали потрібний нам результат.
Приклад
2 ∫ dx=
|додамо і віднімемо і|=∫
dx=
|додамо і віднімемо і|=∫ dx=|ділення
почнемо|=∫
dx=|ділення
почнемо|=∫ dx+2∫
dx+2∫ =∫dx+2∫
=∫dx+2∫ =x+2*
=x+2* ln|
ln| |+c=x+ln|
|+c=x+ln| |+c
|+c
Приклад
3 ∫ =|додамо
х і віднімемо х|=∫
=|додамо
х і віднімемо х|=∫ dx=∫
dx=∫ dx-∫
dx-∫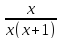 dx=
dx=
=∫ -∫
-∫ =ln|x|-ln|x+1|+c=ln|
=ln|x|-ln|x+1|+c=ln| |+c
|+c
Приклад
4 ∫ =
Додамо
=
Додамо
 і віднімемо
і віднімемо
 і поділимо почлено =∫
і поділимо почлено =∫ dx=
dx=
=∫ dx-∫
dx-∫ dx=∫
dx=∫ -∫
-∫ =|Відносно
другого інтеграла знову додаємо
=|Відносно
другого інтеграла знову додаємо
 і віднімаємо
і віднімаємо
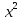 |=∫
|=∫ -∫
-∫ dx=∫
dx=∫ dx-∫
dx-∫ +∫
+∫ =
= +
+ +arctgx+c=
+arctgx+c=
=- +
+ +arctgx+c
+arctgx+c
4. Метод виділення повного квадрату.
Цей метод передбачає спрощення підінтегральної функції шляхом виділення повного квадрата там, де це можливо, для того щоб потім застосувати зміну перемінної. Покажемо це на прикладах
Приклад
1 ∫
В
знаменнику спробуємо виділити повний
квадрат наступним чином ∫ =∫
=∫ =∫
=∫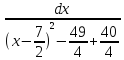 =∫
=∫ =
Тепер ми можемо
внести під знак диференціала -
=
Тепер ми можемо
внести під знак диференціала -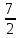 ,
бо де (x-
,
бо де (x- )=dx;
а
)=dx;
а
 дорівнює
дорівнює
 .
Отже маємо ∫
.
Отже маємо ∫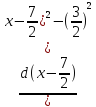 =∫
=∫ =
Якщо зробити заміну х-
=
Якщо зробити заміну х- =t,
dx=dt,
то цей інтеграл табличний №14, де a=
=t,
dx=dt,
то цей інтеграл табличний №14, де a= .
Тому =
.
Тому = ln|-
ln|- |+c=
|+c= ln|
ln| |+c=
|+c= ln|
ln| |+c
|+c
Приклад
2 ∫ =∫
=∫ =
виділяємо
в знаменнику повний квадрат =∫
=
виділяємо
в знаменнику повний квадрат =∫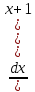 =∫
=∫ =|це
вже ми отримали табличний інтеграл
відповідно формулі №13. Тому маємо|=
=|це
вже ми отримали табличний інтеграл
відповідно формулі №13. Тому маємо|= arctg
arctg +c
+c
Приклад
3 ∫ =
Виділяємо
в знаменнику повний квадрат для того,
щоб звести його до табличної формули
№12 =∫
=
Виділяємо
в знаменнику повний квадрат для того,
щоб звести його до табличної формули
№12 =∫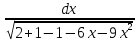 =∫
=∫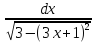 =
= ∫
∫ =
= ∫
∫ =
Останній
вираз вже відповідає табличному інтегралу
по формулі №12 і тому остаточно маємо:
=
=
Останній
вираз вже відповідає табличному інтегралу
по формулі №12 і тому остаточно маємо:
= arcsin
arcsin +c.
+c.
5. Метод невизначених коефіцієнтів
Суть цього метода полягає в тому, що знаменник дробі підінтегральної функції представляємо як добуток множників і дорівнюємо заданий інтеграл сумі інтегралів, в яких у знаменниках стоять ті самі множники, а в чисельниках поки невідомі коефіцієнти. Дорівняємо підінтегральні функції з обох частин із цього равенства знаходимо невідомі коефіцієнти, а потім і самі інтеграли.
Розглянемо застосування цього метода на прикладах. І почнемо з приклада який ми вже розглядали іншим методом.
Приклад
1. ∫ =∫
=∫ =
Тепер вводимо невідомі коефіцієнти A
i
B
наступним чином =∫
=
Тепер вводимо невідомі коефіцієнти A
i
B
наступним чином =∫ +∫
+∫ .
Така зміна передбачає равенство дробів
.
Така зміна передбачає равенство дробів
 =
= +
+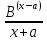 =
=
Далі
дорівнюємо чисельники
O*x+1*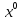 =Ax+Aa+Bx-Ba=x(A+B)+
=Ax+Aa+Bx-Ba=x(A+B)+ (Aa-Ba)
таке рівняння тільки в тому випадку,
якщо коефіцієнти при х в однаковій
степені зліва і справа дорівнює одне
одному. Тобто А+В=0 В=-А
(Aa-Ba)
таке рівняння тільки в тому випадку,
якщо коефіцієнти при х в однаковій
степені зліва і справа дорівнює одне
одному. Тобто А+В=0 В=-А
Аа-Вa=1
Aa+Aa=1 A= ,
B=-
,
B=-
Підставляємо
значення знайдення коефіцієнтів
∫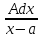 +∫
+∫ =
=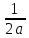 ∫
∫ -
-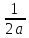 ∫
∫ =
=
= ln|x-a|-
ln|x-a|- ln|x+a|+c=
ln|x+a|+c= ln|
ln| |+c
|+c
Ми отримали той самий результат тільки вже методом невизначених коефіцієнтів.
Приклад
2. ∫ =∫
=∫ +∫
+∫
Шукаємо коефіцієнти А і В так, як і в попередньому прикладі
 -
- +
+ =
=
Тепер дорівнюємо чисельники зліва і справа 1=2Ах-3А+Вх+В Дорівнюємо коефіцієнти зліва і справа при х в однаковій степені і отримуємо два рівняння
2А+В=0 В=-2А
-3А+В=1
-5А=1 A=- ;
B=
;
B=
Підставляємо
ці коефіцієнти в інтеграли ∫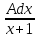 +∫
+∫ =-
=- ∫
∫ +
+ ∫
∫ =
=
=- ∫
∫ +
+ ∫
∫ =-
=- ln|x+1|+
ln|x+1|+ ln|2x-3|=
ln|2x-3|= ln|
ln| |+c
|+c
Приклад 3
Далі знову вводимо невизначені коефіцієнти
Дорівнюємо підінтегральні функції зліва і справа, та приводимо вираз справа до загального знаменника
Дорінюємо чисельники та знаходимо коефіцієнти А і В
Підставляємо значення А і В в інтеграли та знаходимо їх
Слід зазначити, що цей інтеграл можна звести до табличного №14, а саме
Останній вираз уявляє собою табличний інтеграл по формулі №14 і тому
Як ми бачимо, іноді існують навіть декілька способів одного й того ж інтеграла.
Далі ми перейдемо до одного з основних методів рішення невизначених інтегралів.
