
Основні методи інтегрування
Почнемо розглядати з метода заміни перемінної, який ми фактично вже застосували.
-
Метод заміни перемінної
Головна задумка цього методу - це підібрати нову перемінну таким чином, щоб спростити інтеграл чи зразу звести його до табличного.
В загальному вигляді це буде так:
∫f(x)dx=| вибираємо нову перемінну t=φ(x) чи відносно x=φ(t) диференціюємо φ’(t)dt і підставляємо =∫f[φ(t)]φ’(t)dt=F(t)+c= |
Якщо за рахунок цього дійства є спрощення, то знаходимо первісну функцію і замість нової перемінної t підставляємо її значення.
=F[φ(x)]+c і це вже маємо рішення.
розберемо цей метод на прикладах. При цьому виділимо три випадки
1.1 Заміна лінійної функції
Приклад
1 ∫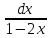
Робимо
заміну таким чином t=1-2x,
a
x=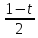
Диференціюємо
останнє dx=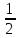 (-dt),
a
dt=-2d
(-dt),
a
dt=-2d
Все це підставляємо в задані інтеграли
∫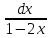 =-
=-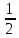 ∫
∫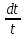 =|
а це вже табличний інтеграл
=-
=|
а це вже табличний інтеграл
=-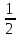 ln|t|+c=ln|
ln|t|+c=ln| |+c=ln|
|+c=ln|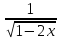 |+c
|+c
Приклад
2 ∫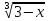 dx
dx
Вибираємо заміну t=3-x, a x=3-t
Дані диференцюємо dx=-dt і підставляємо
∫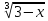 dx=-∫
dx=-∫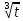 =-∫
=-∫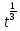 dt=-
dt=-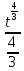 +c=-
+c=-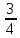 t
t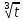 +c=-
+c=-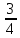 (3-x)
(3-x)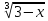 +c
+c
Приклад
3 ∫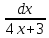 Знову робимо заміну t=4x+3,
a
x=
Знову робимо заміну t=4x+3,
a
x=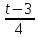 ;
диференціюємо dx=
;
диференціюємо dx= dt
і підставляємо ∫
dt
і підставляємо ∫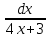 =
=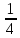 ∫
∫ =
=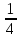 ln|
ln|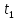 +c=ln|
+c=ln|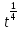 |+c=ln|
|+c=ln|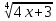 |+c
|+c
Приклад
4 ∫ dx.
Робимо таку ж заміну t=-2x+7,
a
x=
dx.
Робимо таку ж заміну t=-2x+7,
a
x= ,
диференцюємо dx=-
,
диференцюємо dx=-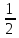 dt
і вже це підставляємо ∫
dt
і вже це підставляємо ∫ =-
=-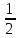 ∫
∫ dt=
(а це вже таблічний інтеграл)=-
dt=
(а це вже таблічний інтеграл)=-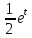 +c=-
+c=-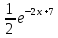 +c
+c
1.2. Заміна нелінійної функції
Приклад
1 ∫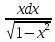 .
Вибираємо заміну t=1-
.
Вибираємо заміну t=1-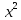 ,
чи
,
чи
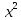 =1-t
і диференцюємо останнє рівенство
2xdt=-dt
або xdx=-
=1-t
і диференцюємо останнє рівенство
2xdt=-dt
або xdx=-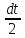
все це підставляємо в заданий інтеграл
∫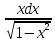 =-
=-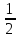 ∫
∫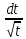 =-
=-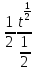 +c=-
+c=-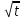 +c=-
+c=-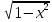 +c
+c
приклад
2 ∫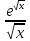 dx.
Робимо заміну t=
dx.
Робимо заміну t=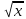 чи x=
чи x=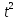 дифеенцюємо dx=2tdt
і підставляємо ∫
дифеенцюємо dx=2tdt
і підставляємо ∫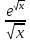 dx=∫
dx=∫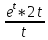 dt=2∫
dt=2∫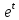 dt=2
dt=2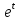 +c=2
+c=2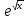 +c
+c
Приклад
3 ∫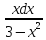 .
робимо заміну 3-
.
робимо заміну 3-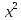 =t
та диференцюємо це рівенство
=t
та диференцюємо це рівенство
-2xdx=dt,
чи xdx=-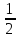 dt
Все це підставляємо
∫
dt
Все це підставляємо
∫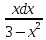 =-
=-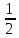 ∫
∫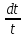 =-
=-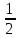 ln|t|+c=-ln|
ln|t|+c=-ln|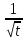 |+c=ln|
|+c=ln|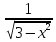 |+c
|+c
Приклад
4 ∫ dx
dx
Робимо
заміну t=3+5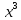 і диференціюємо 15
і диференціюємо 15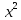 dx=dt,
чи
dx=dt,
чи
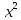 dx=
dx=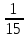 dt.
Підставляємо:
∫
dt.
Підставляємо:
∫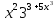 dx=
dx=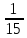 ∫
∫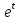 dt=
dt=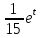 +c=
+c=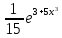 +c.
+c.
1.3 Заміна функції шляхом перетворення під знаком диференціала.
Така заміна під знаком диференціала є різновидністю метода заміни перемінної. вона застосовується тоді, коли ця заміна очевидна. Покажемо це на прикладах:
Приклад 1 ∫cos(3x+2)dx
Щоб
звести такий інтеграл до табличного,
треба продиференціювати d(3x+2)=3dx,
а dx=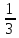 d(3x+2)
d(3x+2)
Тому
∫cos(3x+2)dx=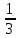 ∫cos(3x+2)d(3x+2)=sin(3x+2)+c
∫cos(3x+2)d(3x+2)=sin(3x+2)+c
Приклад
2 ∫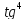 xdx
xdx
Для
зведення цього інтеграла до табличного
нам потрібно мати d(4x).
Диференціюємо це d(4x)=4dx,
а dx=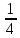 d(4x).
Тоді маємо ∫tg4xdx=
d(4x).
Тоді маємо ∫tg4xdx=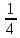 ∫tg4xd(4x)=
∫tg4xd(4x)=
=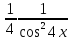 +c.
+c.
2. Метод зведення неправильної дробі до правильної.
Суть
цього метода ми почнемо розглядати
після введення визначення правильної
та неправильної дробі. В загальному
вигляді раціонально дріб є відношенням
многочленів
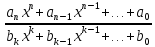
якщо n<k, то дроб правильна
а при n>k дроб неправильна.
Метод зведення підінтегральної функції від неправильної дробі до правильної дробі передбачає ділення многочлена-чисельника на многочлен-знаменник, якщо така дія спрощує рішення. Яким чином це робиться розглянемо на прикладах.
Приклад
1 ∫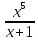 dx.
Це неправильна дроб, бо 5>1.
Зробимо ділення
dx.
Це неправильна дроб, бо 5>1.
Зробимо ділення
ТУТ ПОВИННЕ БУТИ ДІЛЕННЯ В СТОВПЧИК
Заданий
інтеграл таке ділення дозволяє звести
до вигляду:
∫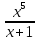 dx=
dx=
=∫(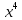 -
- +
+ -x+1-
-x+1-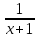 )dx=
який
легко вирішується = ∫
)dx=
який
легко вирішується = ∫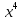 dx-∫
dx-∫ dx+∫
dx+∫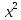 dx-
dx-
-∫xdx+∫dx-∫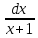 =
=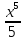 -
-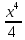 +
+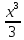 -
-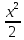 +x-ln|x+1|+c
+x-ln|x+1|+c
Слід
зазначити, що якщо результат такого
ділення привести до загального знаменника,
то ми отримуємо задану функцію в
начальному вигляді
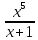
Приклад
2 ∫ dx.
Це теж неправильно дроб робимо ділення
dx.
Це теж неправильно дроб робимо ділення
ТУТ ПОВИННЕ БУТИ ДІЛЕННЯ В СТОВПЧИК
Спрощуємо
заданий інтеграл і вирішуємо
його:
∫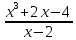 dx=∫(
dx=∫(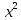 +2x+6+
+2x+6+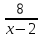 )dx=∫
)dx=∫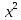 dx+∫2xdx+∫6dx+∫
dx+∫2xdx+∫6dx+∫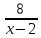 dx=
dx= +
+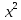 НІЧОГО
НЕ ВИДНО
НІЧОГО
НЕ ВИДНО
Приклад
3 ∫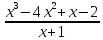 dx.
Це
теж неправильно дроб. Ділимо і вирішуємо
цей інтеграл.
dx.
Це
теж неправильно дроб. Ділимо і вирішуємо
цей інтеграл.
ТУТ ПОВИННЕ БУТИ ДІЛЕННЯ В СТОВПЧИК
Підставляємо
результат ділення в заданий інтеграл
та легко знаходимо його
∫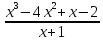 dx=∫(
dx=∫(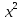 -5x+6-
-5x+6-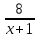 )dx=∫
)dx=∫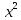 dx-∫5xdx+∫6dx-∫
dx-∫5xdx+∫6dx-∫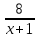 dx=
dx=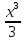 -5
-5 +6x-8ln|x+1|+c
+6x-8ln|x+1|+c
