Смешанные типы

B1. Область допустимых решений задачи линейного программирования имеет вид

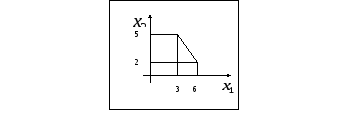
Тогда максимальное значение целевой функции равно

• 13

• 10

• 14

• 11

Решение: Для ограниченной выпуклой области и линейной целевой функции достаточно подставить угловые точки ив функцию и выбрать максимальное значение. Максимальным значением будет.

B2. Матрица выигрышей в игре с природой имеет вид

.

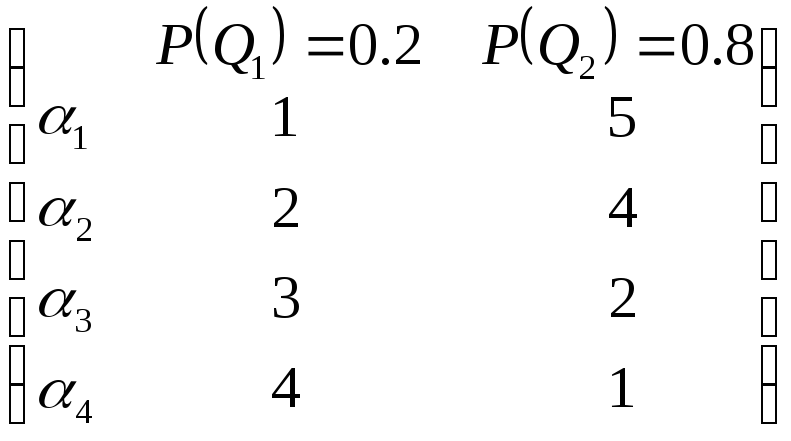Тогда наибольший средний выигрыш достигается при применении стратегии

• 

• 

• 

• 

Решение: Вычислим математическое ожидание (среднее значение) выигрыша каждой стратегии:

Следовательно, наилучшей стратегией (ответствующей максимальному среднему) является стратегия .

B3. Для сетевого графика, изображенного на рисунке

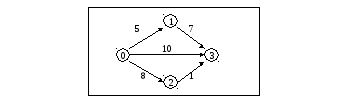
длина критического пути равна

• 12

• 10

• 9

• 31

Решение: Длиной критического пути для нагруженного орграфа называют максимальную возможную длину. Для данного графа путь 0-1-3 имеет длину 5+7=12; путь 0-3 имеет длину 10, путь 0-2-3 имеет длину 8+1=9. Других путей нет, следовательно, критическим является путь 0-1-3, длины 12.

B4. Максимальное значение целевой функции при ограничениях

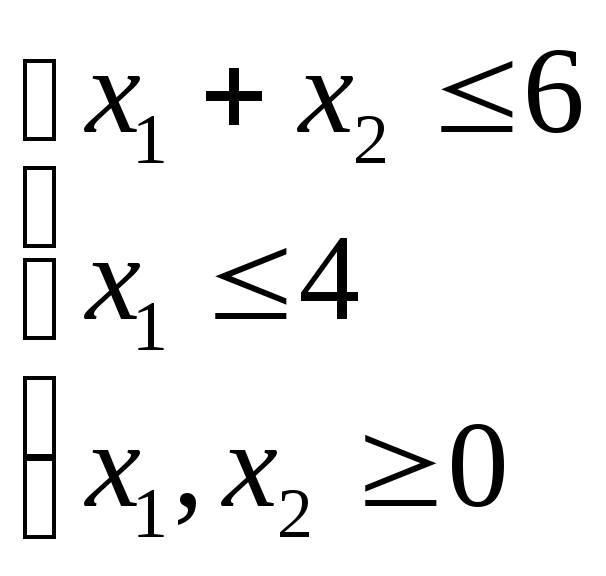
равно

• 6

• 12

• 13

• 8

Решение: Построим выпуклую область, заданную в условии системой линейных неравенств

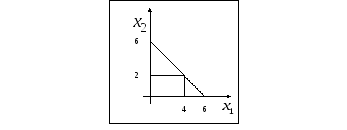
Вычислим значение целевой функции в угловых точках и, максимальным из которых будет.

B5. Транспортная задача

	50	60+b	200
100+а	7	2	4
200	3	5	6

будет закрытой, если

• 

• 

• 

• 

Решение: Транспортная задача называется закрытого типа, если объем поставляемых ресурсов (сумма в левом столбце) равен объему распределяемых ресурсов (сумма в первой строке): , откуда получаем. Данному соотношению удовлетворяет лишь третий вариант ответа.

B6. Даны множества ицелых чисел. Тогда разностьесть

• 

• 

• 

• 

Решение: Разность означает, что из множестванеобходимо удалить элементы множества, т.е. востанутся только нецелые числа. В итоге=.

B7. Реализацией графа с множеством вершин и списком дугявляется

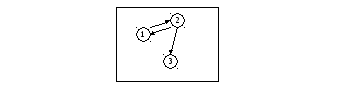
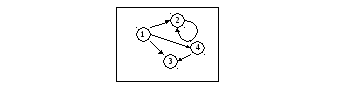
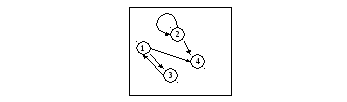
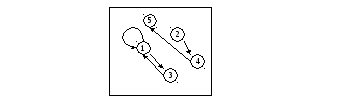
Решение: Выберем те графы, в которых присутствует лишь четыре вершины и пять дуг(т.е. второй и третий варианты ответов). Далее убедимся, что каждой дуге, объявленной в, соответствует стрелка, исходящая из вершины первой координаты дуги и приходящая во вторую: например, дугедолжна соответствовать стрелка из вершины 1 в вершину 4, а для дугидолжна быть отображена стрелка-петля из вершины 2 в саму себя. Проверяя подобным образом каждую дугу, приходим к заключению, что верным оказывается третий вариант.

B8. Три итерации метода половинного деления при решении уравнения на отрезкетребуют последовательного вычисления значений функциив точках

• 

• 

• 

• 

Решение: в методе половинного деления каждая последующая точка итерации выбирается как середина предыдущего отрезка, для которого функция принимает различные знаки на концах. Проделаем эту процедуру, начиная с отрезка :

Первая точка середина :. Отрезок разбит на две половины:и. Для первого отрезка функция принимает различные знаки на концах:и.

Вторая точка середина отрезка :. Отрезок разбит на две половины:и. Для первого отрезка функция принимает различные знаки на концах:и.

Третья точка середина отрезка :.

В итоге, верным является второй вариант ответа .

В9. Дан радиус-вектор движения точки в пространстве , тогда вектор ускорения точки в момент времениравен

• 

• 

• 

• 

Решение: Вектор можно записать в координатной форме как. Вычисляя вторую производную поот координат, получим:

. Тогда при имеем:, т.е..

41