Теория вероятностей

V1. Случайные события и, удовлетворяющие условиям,и, являются

• Несовместными и независимыми

• Несовместными и зависимыми

• Совместными и независимыми

• Совместными и зависимыми

Решение: События очевидно совместны, т.к. вероятность одновременного наступления событий иотлична от нуля. Для проверки независимости воспользуемся (в случае двух событий) критерием:. Подставляя, убеждаемся, что. Следовательно, события зависимы.

V2. Монета брошена 4 раза. Тогда вероятность, что орел выпадет хотя бы 1 раз равна

• 

• 

• 

• 

Решение: .P.S. Здесь было использовано, что броски по смыслу задачи независимы.

V3. Распределение появления события в 20 независимых испытаниях, проведенных по схеме Бернулли, равно. Тогда математическое ожидание числа появления этого события равно

• 

• 

• 

• 

Решение: Обозначим ,и. Тогда математическое ожидание.

Замечание. Дисперсия числа появления события равна.

V4. Непрерывная случайная величина задана плотностью распределения вероятности, тогда математическое ожидание этой нормально распределенной случайной величины равно

• 18

• 3

• 4

• 9

Решение: Для нормально распределенной случайной величины с параметрами (математическое ожидание) и(среднее квадратическое отклонение) функция плотности имеет вид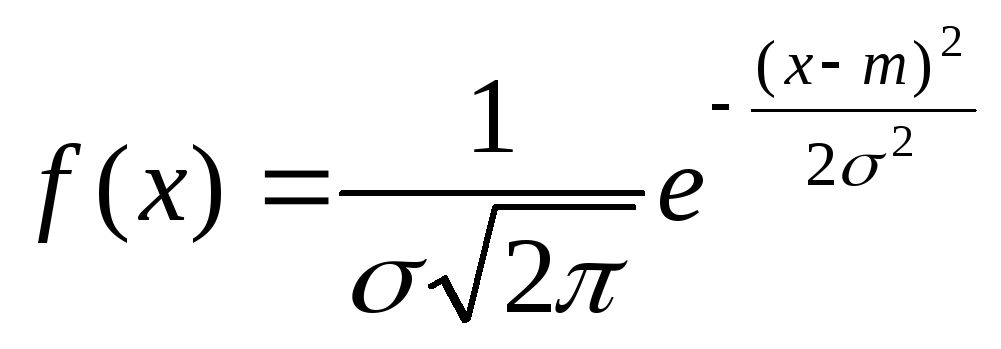. Сравнивая с данными условия, находим.

Замечание. Дисперсия в данном задании вычисляется как .

V5. Вероятность достоверного события равна

• 

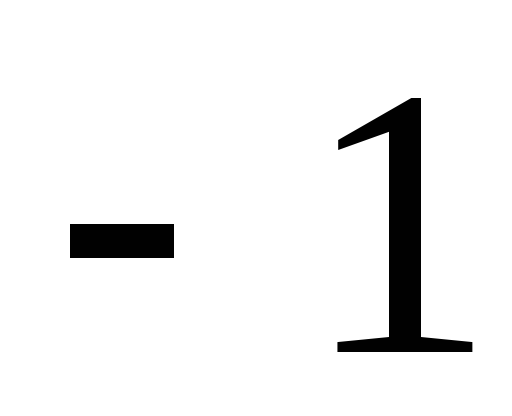
• 0

• 1

• 

Решение: Вероятность достоверного события по определению равна 1.

Замечание. Вероятность невозможного события по определению равна 0.

V6. По оценкам экспертов вероятности банкротства двух предприятий, производящих разнотипную продукцию, соответственно равны и. Тогда вероятность банкротства обоих предприятий равна

• 

• 

• 

• 

Решение: Учитывая. Что предприятия могут обанкротиться независимо друг от друга (на это указывает условия о разнотипности продукции), используем формулу для независимых событий .

V7. Случайная величина распределена равномерно на . Тогда ее математическое ожидание и дисперсия равны

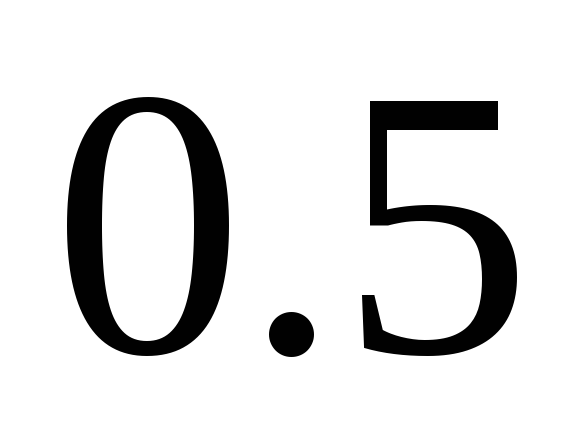• и

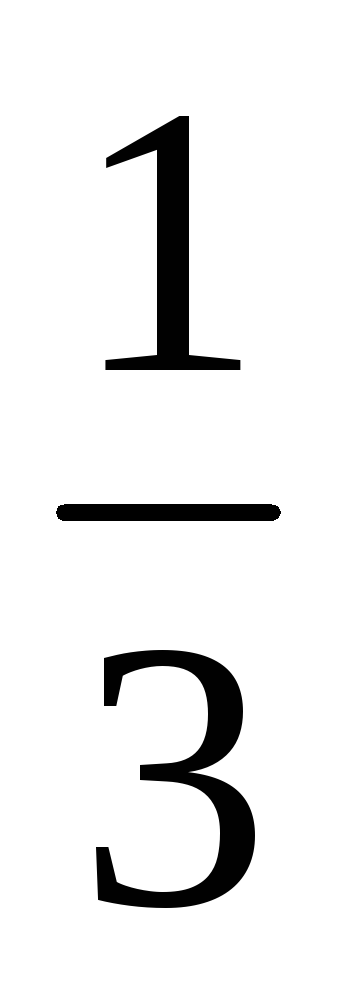
• 10 и

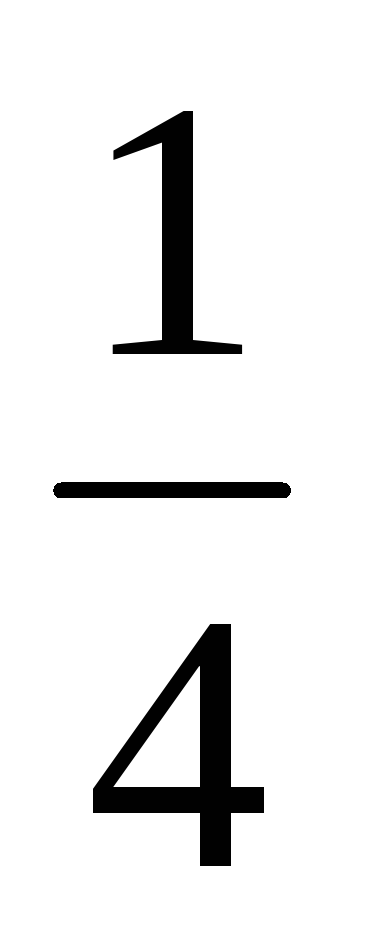
• 11 и

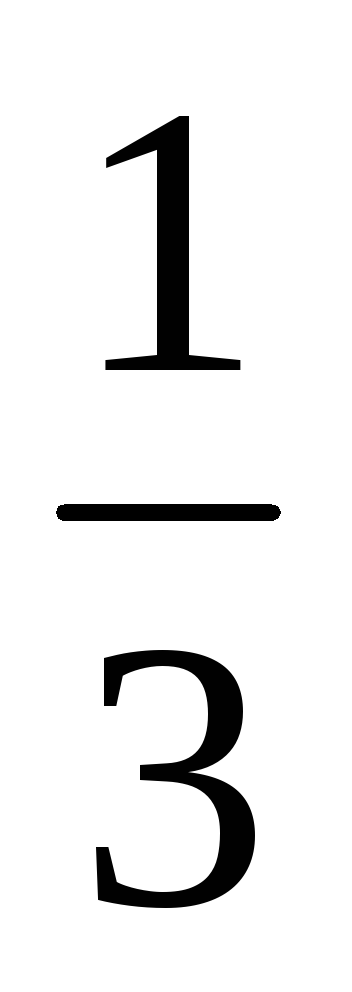
• 11 и 1

Решение: Для равномерно распределенной случайной величины на интервале(или отрезке) имеем:и.

V8. Несовместные события иобразуют полную группу, если их вероятности равны

• 

• 

• 

• 

Решение: Несовместные события иобразуют полную группу, если сумма их вероятностей равна 1. Проверкой убеждаемся, что верным является первый вариант.

V9. Из урны, содержащей 5 белых и 2 черных шара, вынули 4 шара. Вероятность того, что все они оказались белыми равна

• 

• 

• 

• 

Решение: Учитывая, что события зависимы используем общую формулу (при вычислении условных вероятностей считают, что событие «стоящее внизу» достоверно наступило, т.е. вынутый шар уменьшает количество оставшихся белых и общее количество шаров).

V10. Страхуется 1200 автомобилей. Считается, что каждый из них может попасть в аварию с вероятностью 0.08. Для вычисления вероятности, что количество аварий среди всех застрахованных автомобилей не превзойдёт 100, следует использовать

• Формулу полной вероятности

• Формулу Пуассона

• Интегральную формулу Муавра-Лапласа

• Формулу Байеса

Решение: Здесь речь идёт о схеме Бернулли с параметрами и(). Вероятность, что количество успеховне превзойдёт 100, можно записать как. Наличие интервала уже говорит об интегральной формуле Муавра-Лапласа. Для строгости рассуждений проверим условие применимости:- верно.

Замечание. Для локальной формулы Муавра-Лапласа, когда речь идет об одном значении , условие применимостиследует различать с условием применимости для формулы Пуассона. В обоих случаях предельные теоремы применяются при больших.

V11. В группе 20 студентов. Тогда число способов выбрать среди них старосту и его заместителя равно

• 39

• 210

• 400

• 380

Решение: По правилу произведения - старосту можно выбрать 20 способами, а при выбранном старосте заместителя можно выбрать 19 способами. Следовательно, общее количество способов выбрать такую пару .