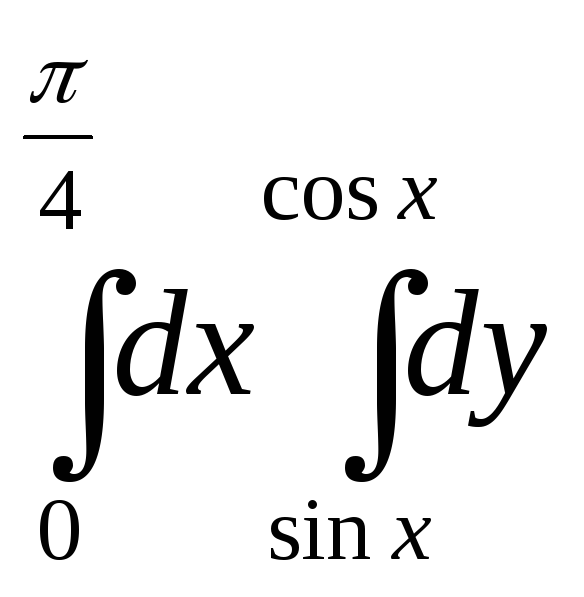- •Федеральное государственное образовательное учреждение высшего профессионального образования
- •Гринева Наталья Владимировна Зададаев Сергей Алексеевич
- •125468, Ленинградский пр-т, 49
- •Содержание
- •Введение
- •Формы тестовых заданий
- •Решение тестовых заданий Линейная алгебра
- •Аналитическая геометрия
- •Математический анализ
- •Теория вероятностей
- •Математическая статистика
- •Экономические приложения
- •Смешанные типы
Математический анализ
М1.
Количество целых значений
![]() из области определения функции
из области определения функции![]() равно
равно
5
4
6
3
Решение: ОДЗ:
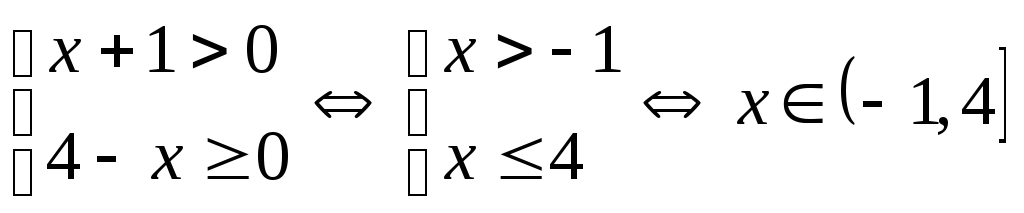 .
Целых значений на области 5 штук.
.
Целых значений на области 5 штук.
М2.
Значение производной функции
![]() в
точке
в
точке![]() равно
равно
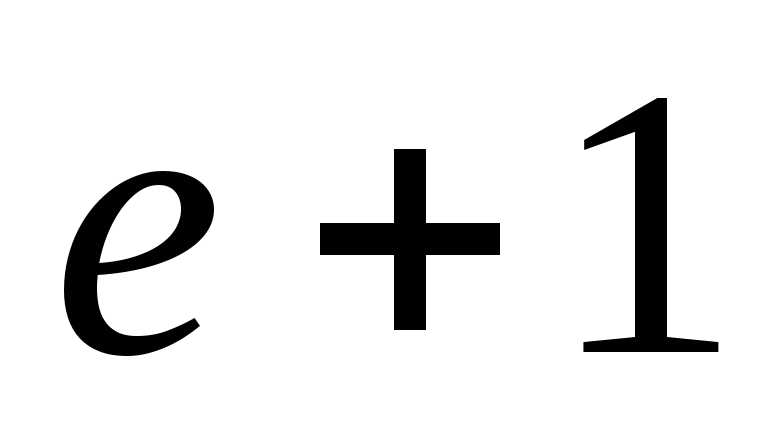
2
-2
0
Решение:
![]() .
Подставляя
.
Подставляя![]() ,
получим:
,
получим:![]() .
.
М3. На рисунке
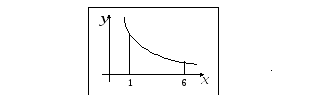
изображен график
функции
![]() ,
заданной на интервале
,
заданной на интервале![]() .
Тогда на этом интервале выполняются
неравенства
.
Тогда на этом интервале выполняются
неравенства
Решение: 1) график
расположен выше оси
![]() ,
следовательно,
,
следовательно,![]() ;
;
2) функция на
интервале убывает, следовательно,
![]() ;
;
3) приведенная
функция является выпуклой, т.к. график
лежит выше касательных, проведенных в
любой точке интервала
![]() ,
что означает
,
что означает![]() или ассоциативное правило: график похож
на часть улыбки «
или ассоциативное правило: график похож
на часть улыбки «![]() ».
».
Замечание. Для
вогнутости (![]() )
график лежит ниже любой касательной
или похож на часть недовольного смайлика
«
)
график лежит ниже любой касательной
или похож на часть недовольного смайлика
«![]() ».
».
М4. Первообразными
функции
![]() являются
являются
Решение: Вычислим
неопределенный интеграл
![]() ,
который является совокупностью всех
первообразных:
,
который является совокупностью всех
первообразных:
![]()
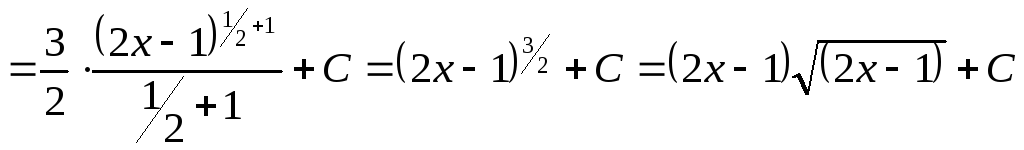 .
.
Сравнивая предложенные варианты ответов, приходим к выводу, что верными являются первый и третий варианты.
Замечание. Можно
было бы продифференцировать каждый из
предложенных ответов и сравнить с
исходной (подинтегральной) функцией
![]() .
.
М 5.Если
5.Если
![]() ,
,![]() ,
то интеграл
,
то интеграл![]() равен
равен
Решение: Используем
линейные свойства определенного
интеграла:
![]() .
Далее подставим данные значения
интегралов и получим:
.
Далее подставим данные значения
интегралов и получим:
![]()
М 6.Положительный
корень
6.Положительный
корень
![]() уравнения
уравнения![]() равен
равен
Решение: Вычислим несобственный интеграл с переменным нижним пределом:
![]() .
.
Приравнивая
интеграл к
![]() ,
получим уравнение:
,
получим уравнение:![]() ,
т.е.
,
т.е.![]() (положительный).
(положительный).
М7. Предел
![]() равен
равен
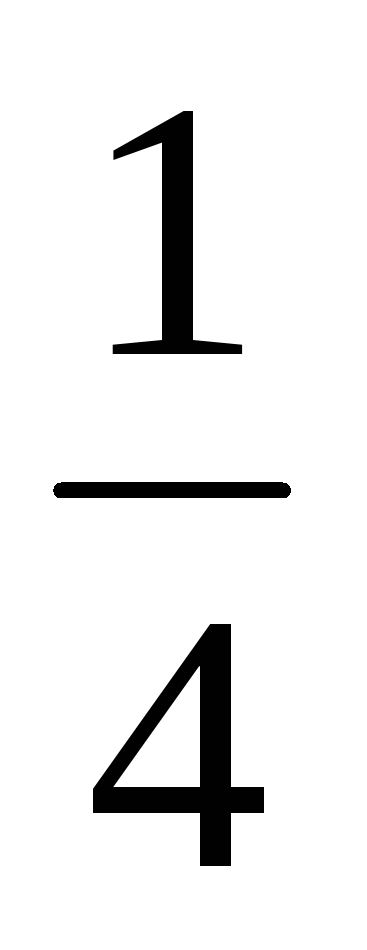
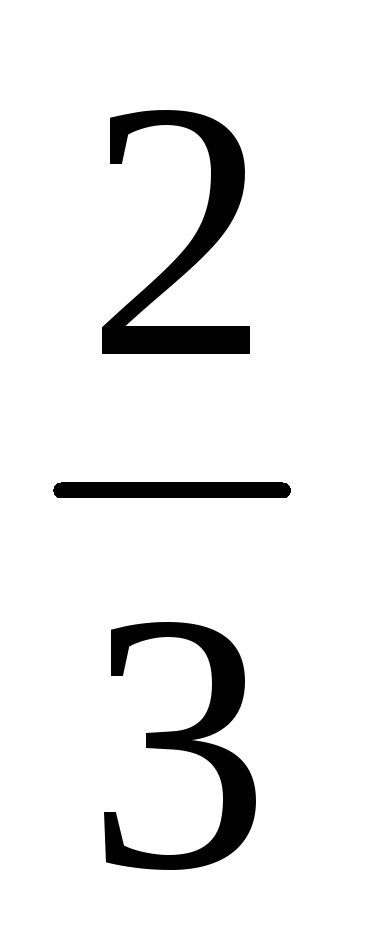
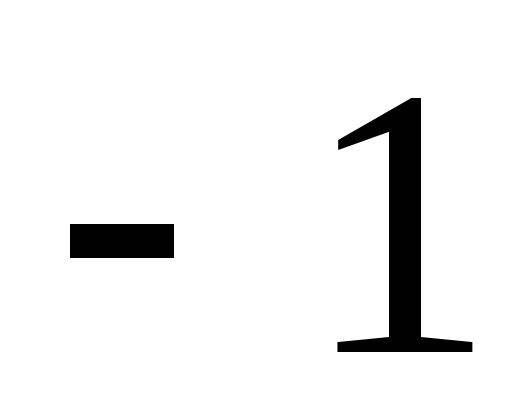
0
Решение:
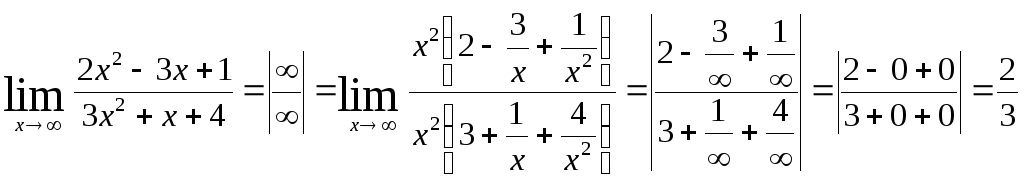 .
.
Замечание. Ответ
можно было бы дать устно, т.к. на
бесконечности можно оставить только
слагаемые старших степеней:
![]() .
.
М8. Дана
функция
![]() ,
тогда областью её значений является
,
тогда областью её значений является
Решение: Найдем
область определения функции:
![]() ,
т.е.
,
т.е.![]() .
Далее вычислим производную функции
.
Далее вычислим производную функции![]() .
На луче
.
На луче![]()
![]() (функция убывает), а на луче
(функция убывает), а на луче![]()
![]() (функция возрастает). Следовательно,
минимальное значение функции может
достигаться в точках
(функция возрастает). Следовательно,
минимальное значение функции может
достигаться в точках![]() или
или![]() :
:![]() .
Максимального значения функция не
достигает, т.к. при
.
Максимального значения функция не
достигает, т.к. при![]() функция
функция![]() также стремится к
также стремится к![]() .
Верным ответом является
.
Верным ответом является![]() .
.
М9. Производная
частного
![]() равна
равна
Решение:
![]() .
.
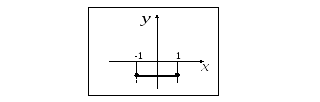
М10. Дан
график производной непрерывной функции,
заданной на
![]()
Тогда эта функция принимает наименьшее значение
в точке 1
в точках 1 и -1 одновременно
в точке -1
в точке 0
Решение: На рисунке
представлен график производной функции
![]() ,
причем, производная отрицательна.
Следовательно, сама функция
,
причем, производная отрицательна.
Следовательно, сама функция![]() убывает,
т.е. большему значению аргумента
соответствует меньше значение функции.
Таким образом, наименьшее значение
достигается в наибольшем аргументе
убывает,
т.е. большему значению аргумента
соответствует меньше значение функции.
Таким образом, наименьшее значение
достигается в наибольшем аргументе![]() .
.
М11.
Множество первообразных функции
![]() имеет вид
имеет вид
Решение:
![]() .
.
М12. Установите соответствие между неопределенным интегралом и разложением подынтегральной функции на элементарные дроби:
○
![]() ○
○
![]()
○
![]() ○
○
![]()
○
![]() ○
○
![]()
○
![]() ○
○
![]()
○
![]()
○
![]()
Решение: Приведем общий вид разложения правильной рациональной функции на элементарные дроби:
1) для случая простого корня
![]()
2) для случая неразложимого квадрата
![]()
Применяя правило, получаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
М13.
Областью интегрирования повторного
интеграла
![]() является прямоугольник
является прямоугольник
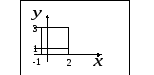
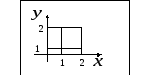
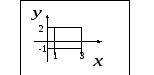
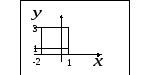
Решение: Из пределов
интегрирования
![]() находим, что
находим, что![]() ,
а
,
а![]() ,
что соответствует прямоугольной области,
изображенной на первом рисунке.
,
что соответствует прямоугольной области,
изображенной на первом рисунке.
М14.
Минимум функции
![]() при условии связи
при условии связи![]() равен
равен
Решение: Выразим
![]() из условия связи:
из условия связи:![]() и подставим в функцию:
и подставим в функцию:![]() .
Найдем минимум функции исследуя её
производную. А именно,
.
Найдем минимум функции исследуя её
производную. А именно,![]() .
Далее
.
Далее![]()
![]() .
Знак производной
.
Знак производной
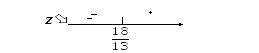
Следовательно, в
точке
![]() функция имеет минимум (локальный).
Значение минимума равно
функция имеет минимум (локальный).
Значение минимума равно![]() .
.
М15.
Наклонной асимптотой графика функции
![]() является
является
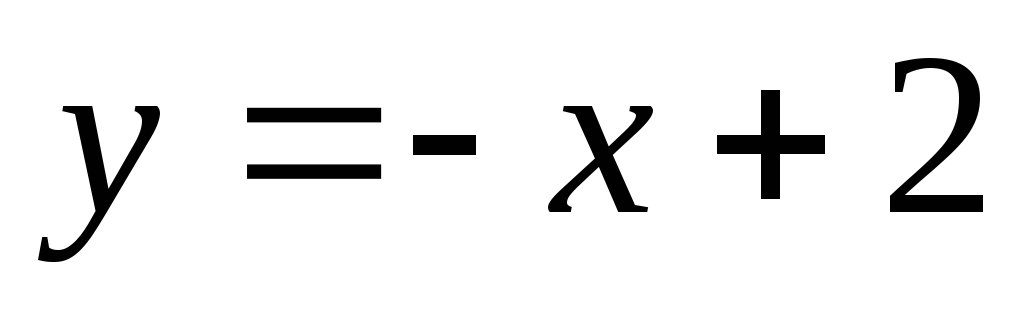
не имеет асимптоты
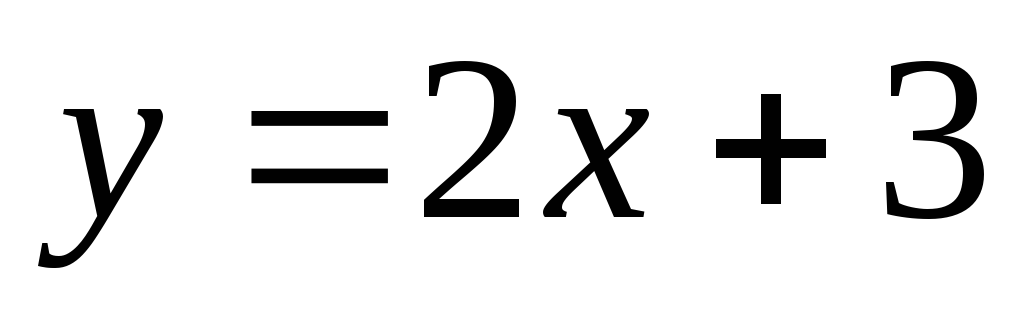

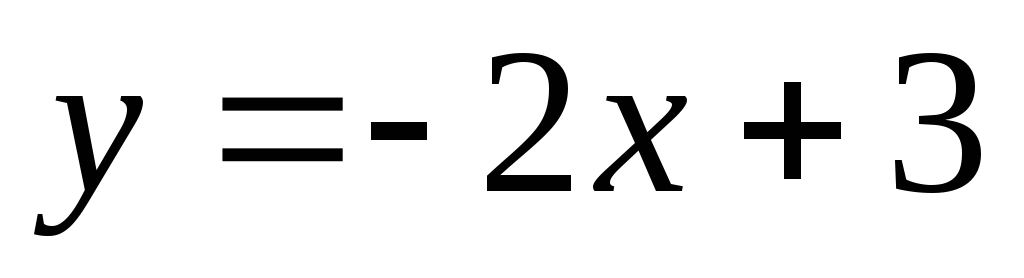
Решение: В данном случае уравнение асимптоты легко получить, выделив целую часть «делением в столбик»:
![]() .
Целая часть и является асимптотой
графика при
.
Целая часть и является асимптотой
графика при
![]() ,
т.е.
,
т.е.![]() .
.
Замечание. В общем
случае уравнения асимптот
![]() при
при![]() к графику функции
к графику функции![]() находятся по формулам
находятся по формулам![]() и
и![]() .
Причем, в формулах понимаются различные
пределы при
.
Причем, в формулах понимаются различные
пределы при![]() и
и![]() ,
что может соответствовать различным
асимптотам.
,
что может соответствовать различным
асимптотам.
М16. Значение
интеграла
![]() равно
равно
Решение:
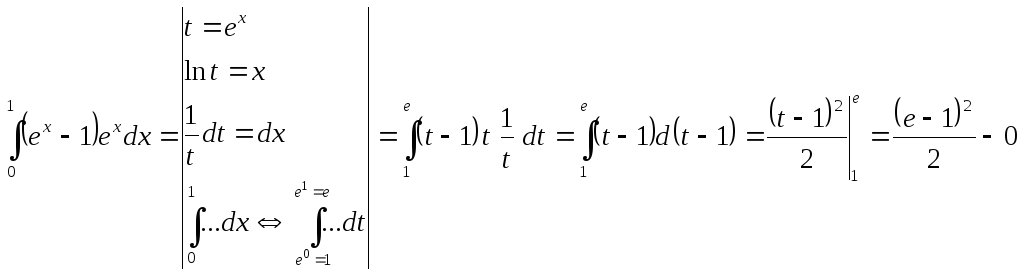
М17.
Площадь области, ограниченная линиями
![]() ,
вычисляется как повторный интеграл
,
вычисляется как повторный интеграл
Решение: Изобразим график области D:
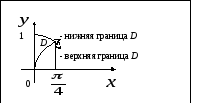
Тогда
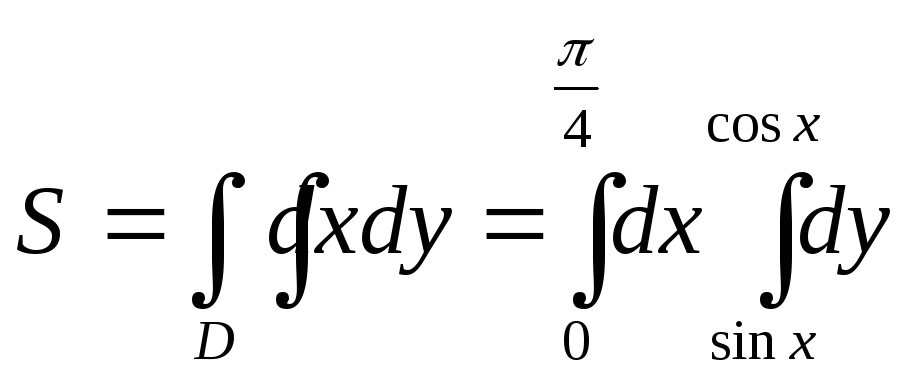 .
Первый интеграл (внешний) по переменной
.
Первый интеграл (внешний) по переменной![]() имеет пределы от
имеет пределы от![]() до
до![]() согласно рисунку. Второй интеграл
(внутренний) по переменной
согласно рисунку. Второй интеграл
(внутренний) по переменной![]() имеет пределы от «нижней» функции (в
данном случае
имеет пределы от «нижней» функции (в
данном случае![]() )
до «верхней» (
)
до «верхней» (![]() .
.
М18. Общий
член последовательности
![]() имеет вид
имеет вид
Решение: Вычислим
![]() с помощью первой формулы
с помощью первой формулы![]() .
Следовательно, первый ответ неверный.
Поступая аналогично с другими вариантами
ответов, получаем, что лишь третья
формула даёт верные ответы для
.
Следовательно, первый ответ неверный.
Поступая аналогично с другими вариантами
ответов, получаем, что лишь третья
формула даёт верные ответы для![]() и
и![]() .
.
М19.
Корень уравнения
![]() равен
равен
Решение: Подставляя
поочередно предложенные корни, приходим,
что верным является лишь
![]() .
.
М20.
Числовой ряд
![]() сходится при всех
сходится при всех![]() ,
удовлетворяющих
,
удовлетворяющих
Решение: Обобщённый
гармонический ряд
![]() сходится при
сходится при![]() и расходится при
и расходится при![]() .
Из условия задачи заключаем, что ряд
.
Из условия задачи заключаем, что ряд![]() сходится при
сходится при![]() .
.
М21.
Сумма числового ряда
![]() равна
равна
Решение: Сумма
геометрической прогрессии
![]() ,
при
,
при![]() .
В нашем случае
.
В нашем случае![]() ,
следовательно,
,
следовательно,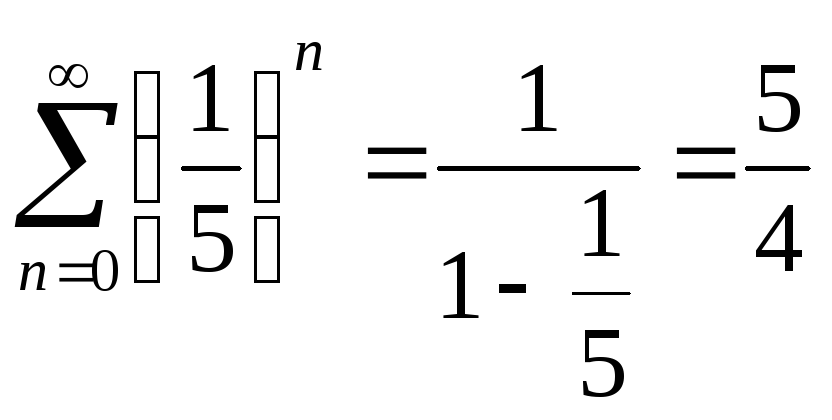 .
.
М22.
Укажите правильное утверждение
относительно сходимости знакочередющихся
рядов А)
![]() и В)
и В)![]() .
.
А и В сходятся условно
А сходится абсолютно, В – расходится
А сходится абсолютно, В – условно
А и В сходятся абсолютно
Решение: Исследуем сходимость каждого ряда
А)
![]() 1) Абсолютная сходимость
1) Абсолютная сходимость![]() .
По второй теореме сравнения (предельной)
заключаем, что
.
По второй теореме сравнения (предельной)
заключаем, что![]() - обобщенный гармонический ряд с
- обобщенный гармонический ряд с![]() сходится. Следовательно, ряд сходится
абсолютно.
сходится. Следовательно, ряд сходится
абсолютно.
В)
![]() .
1) Абсолютная сходимость
.
1) Абсолютная сходимость![]() .
Данный ряд является обобщенным
гармоническим с параметром
.
Данный ряд является обобщенным
гармоническим с параметром![]() - расходится; 2) Условная сходимость
- расходится; 2) Условная сходимость![]() .
Применим признак Лейбница для
знакочередующегося ряда:
.
Применим признак Лейбница для
знакочередующегося ряда:![]() (необходимое условие сходимости
выполнено) и
(необходимое условие сходимости
выполнено) и![]() (члены ряда монотонно убывают),
следовательно ряд сходится. В итоге
заключаем, что ряд сходится условно.
(члены ряда монотонно убывают),
следовательно ряд сходится. В итоге
заключаем, что ряд сходится условно.
М23.
Область сходимости степенного ряда
![]() имеет вид
имеет вид
Решение:
![]() .
.
1)
![]() - радиус сходимости;
- радиус сходимости;
2)
![]() - интервал сходимости;
- интервал сходимости;
3) Проверим концевые точки интервала
![]() Подставим в исходный ряд и получим:
Подставим в исходный ряд и получим:![]() .
Такой ряд расходится, т.к. члены ряда 1,
-1, 1, -1,.. не стремятся к нулю (нарушено
необходимое условие сходимости);
.
Такой ряд расходится, т.к. члены ряда 1,
-1, 1, -1,.. не стремятся к нулю (нарушено
необходимое условие сходимости);
![]() Аналогично получаем
Аналогично получаем
![]() - также расходится, т.к. 1, 1, 1,.. не стремятся
к нулю.
- также расходится, т.к. 1, 1, 1,.. не стремятся
к нулю.
В итоге заключаем,
что область сходимости имеет вид
![]() .
.
М24.
Применяя признак Даламбера
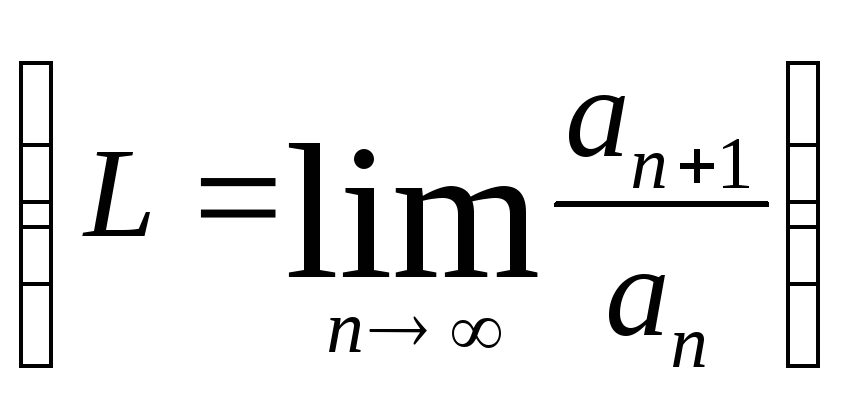 к ряду
к ряду![]() ,
установить верное утверждение
,
установить верное утверждение
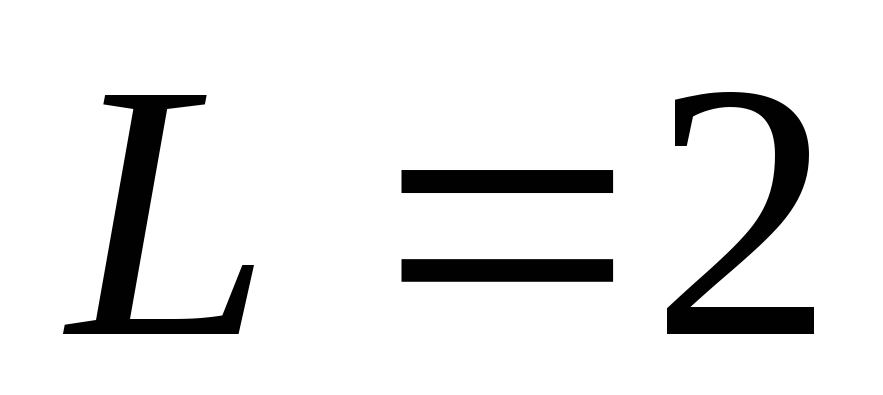 ряд расходится
ряд расходится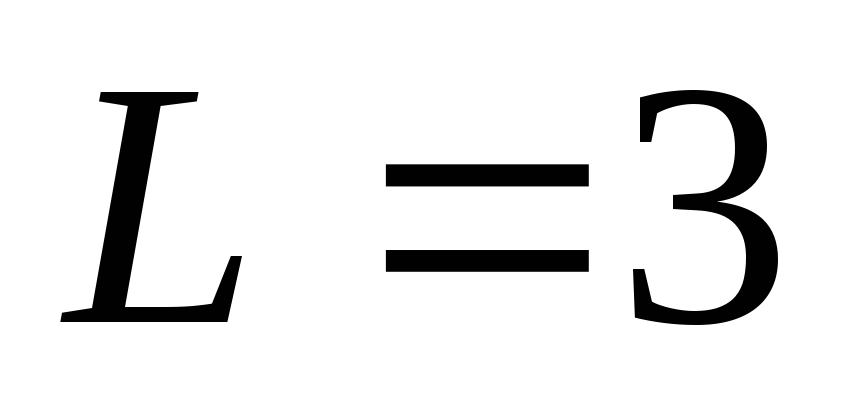 ряд расходится
ряд расходится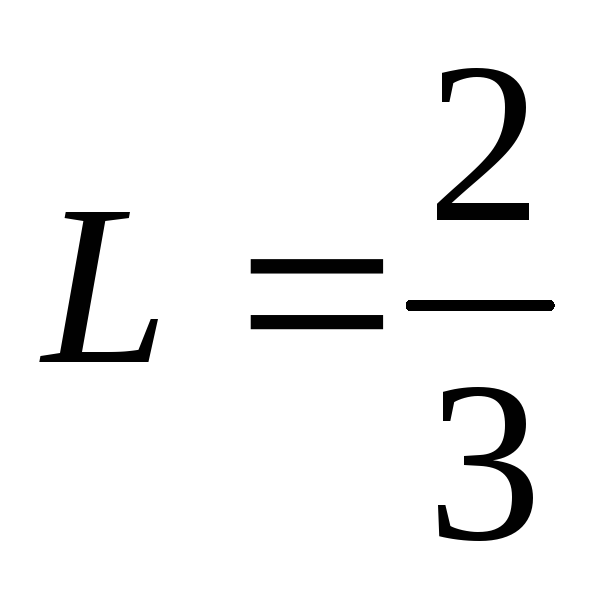 ряд сходится
ряд сходится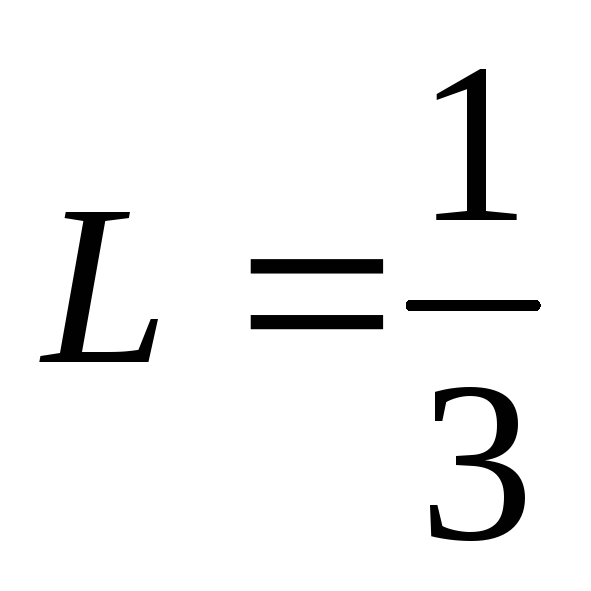 ряд сходится
ряд сходится
Решение: В данном
случае
![]() .
Подставляя в признак Даламбера, получаем:
.
Подставляя в признак Даламбера, получаем:
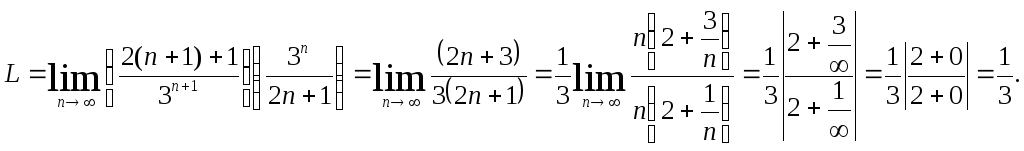
Если
![]() ряд сходится, если
ряд сходится, если![]() ряд расходится. При
ряд расходится. При![]() признак Даламбера оказывается неприменим,
т.к. вопрос о сходимости остаётся
открытым. В нашем случае
признак Даламбера оказывается неприменим,
т.к. вопрос о сходимости остаётся
открытым. В нашем случае![]() ряд сходится.
ряд сходится.
М25. Уравнение
![]() является
является
Линейным неоднородным дифференциальным уравнением первого порядка
Уравнением с разделяющимися переменными
Однородным дифференциальным уравнением
Уравнением Бернулли
Решение: Данное
уравнение может быть приведено к виду
![]() ,
следовательно, оно является однородным
дифференциальным уравнением.
,
следовательно, оно является однородным
дифференциальным уравнением.
Замечание. 1)
Линейным неоднородным дифференциальным
уравнением первого порядка является
![]() ;
2) Уравнение с разделяющимися переменными
имеет вид
;
2) Уравнение с разделяющимися переменными
имеет вид![]() ;
3) Уравнением Бернулли называется
;
3) Уравнением Бернулли называется![]() .
.
М26.
Дано дифференциальное равнение
![]() .
Тогда его решением является
.
Тогда его решением является
Решение: Данное
уравнение можно было бы решить методом
разделения переменных, вычислив
![]() ,
однако предложенные варианты ответов
нетрудно просто подставить в исходное
уравнение. Верным окажется
,
однако предложенные варианты ответов
нетрудно просто подставить в исходное
уравнение. Верным окажется![]() ,
т.к.
,
т.к.![]() и
и![]() - верно.
- верно.
М27. Общий
интеграл дифференциального уравнения
![]() имеет вид
имеет вид
Решение: Вычислим
в методе разделения переменных
![]() .
А именно:
.
А именно:![]() и
и![]() .
Оставляя константу в правой части, в
итоге получаем
.
Оставляя константу в правой части, в
итоге получаем![]() .
.
М28.
Частное решение неоднородного
дифференциального равнения II
порядка
![]() имеет вид
имеет вид
Решение: Напомним,
что общее решение такого уравнения
представляет собой сумму общего решения
![]() однородного уравнения (без правой части
однородного уравнения (без правой части![]() )
и частного решения
)
и частного решения![]() неоднородного (исходного) уравнении.
Продемонстрируем эту схему решения:
неоднородного (исходного) уравнении.
Продемонстрируем эту схему решения:
Однородное уравнение
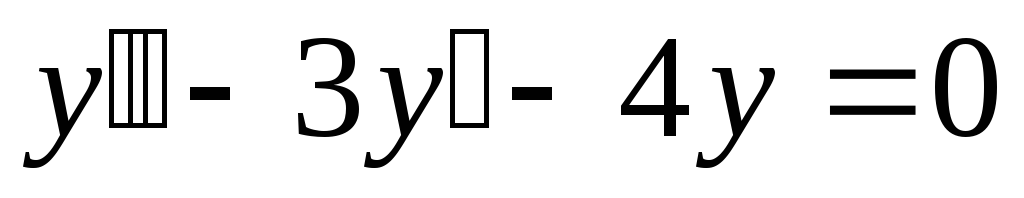 .
Составляем характеристическое уравнение
.
Составляем характеристическое уравнение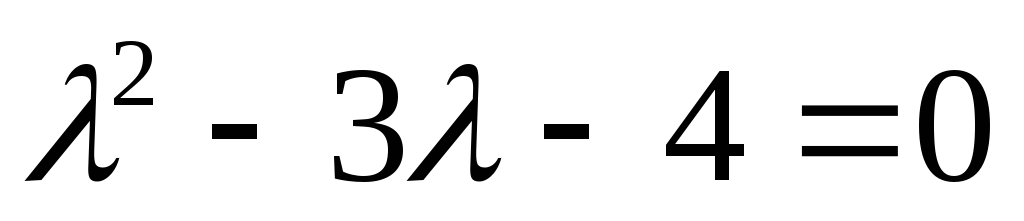 ,
откуда
,
откуда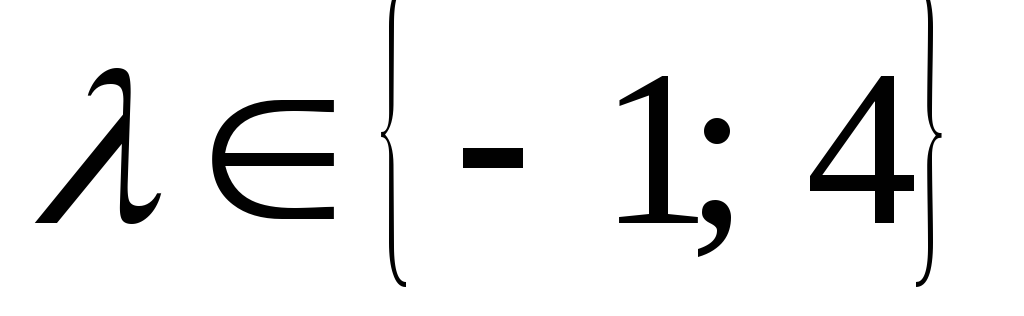 и
и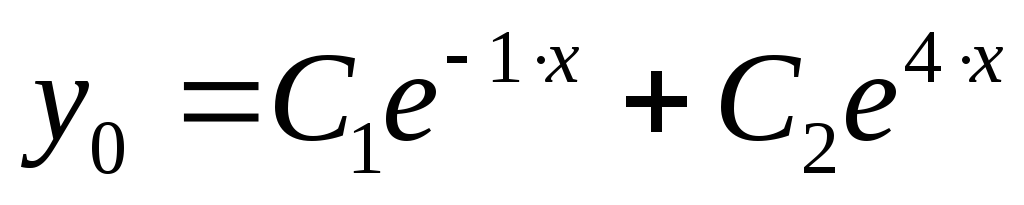 ;
;Неоднородное уравнение
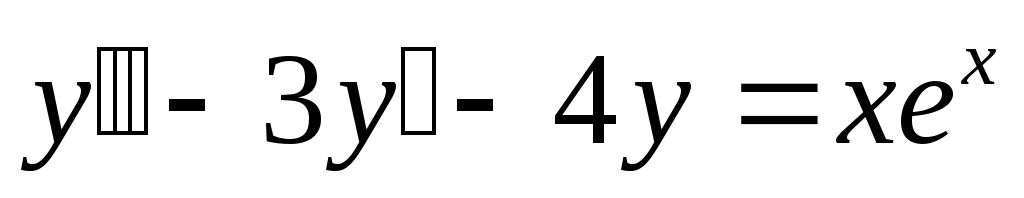 .
Частное решение подбирается по следующему
правилу: многочлен, наблюдающийся в
правой части
.
Частное решение подбирается по следующему
правилу: многочлен, наблюдающийся в
правой части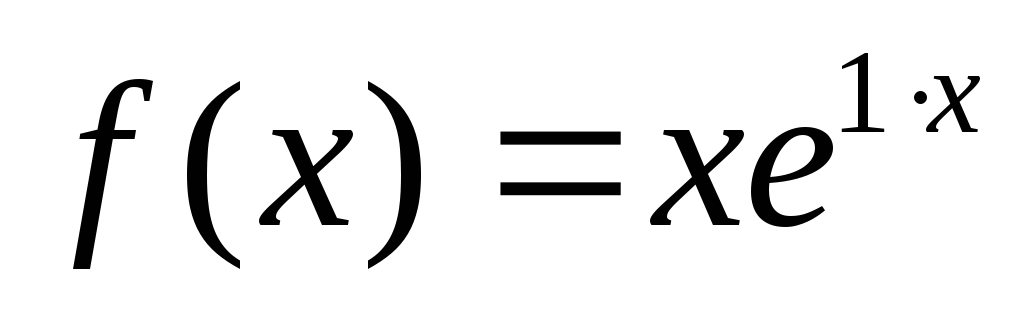 ,
записывается в общем виде
,
записывается в общем виде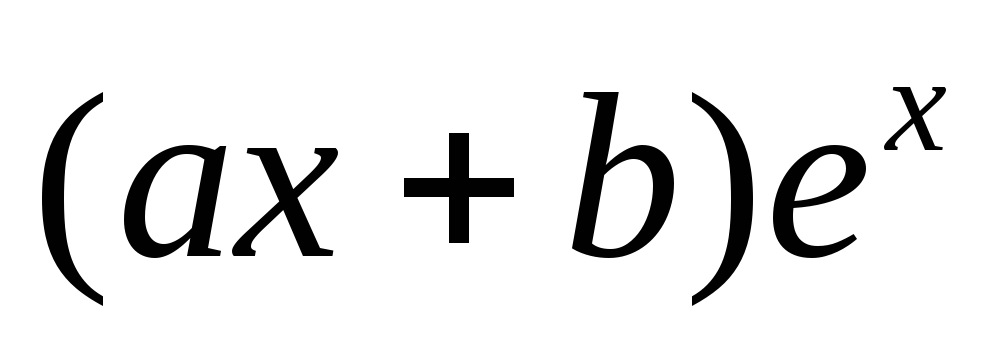 и полученная конструкция умножается
на
и полученная конструкция умножается
на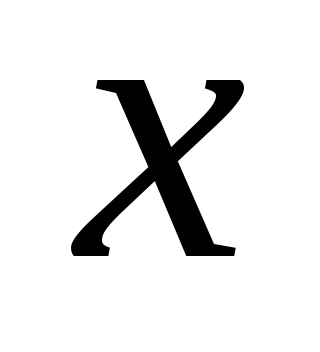 столько раз, сколько раз коэффициент
при
столько раз, сколько раз коэффициент
при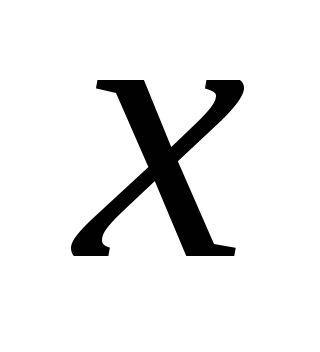 ,
стоящий в экспоненте правой части
,
стоящий в экспоненте правой части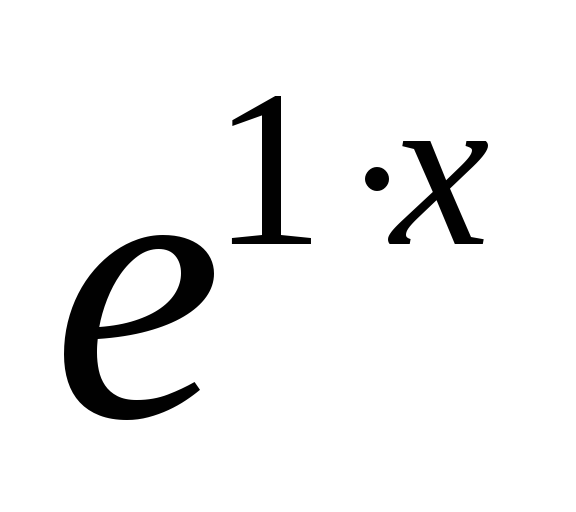 ,
присутствует в найденных ранее
,
присутствует в найденных ранее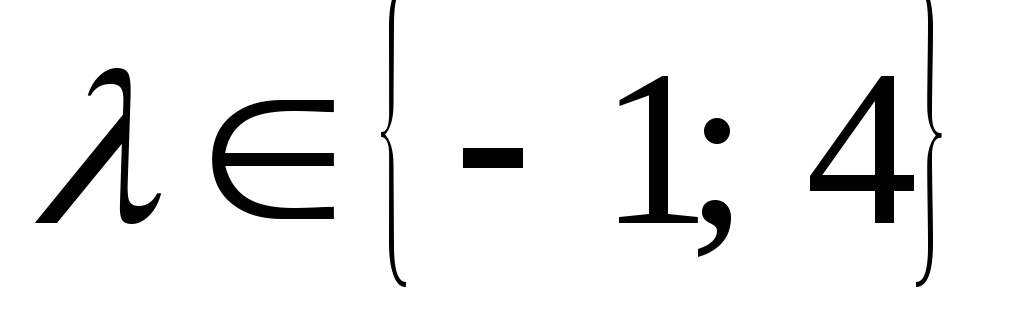 .
В данном случае
.
В данном случае .
т.е. на
.
т.е. на домножать не требуется.
домножать не требуется.
В итоге
![]() .
.
М29.
Частное решение неоднородного
дифференциального равнения II
порядка
![]() имеет вид
имеет вид
Решение: Действуя аналогично примеру М27, получим
Однородное уравнение
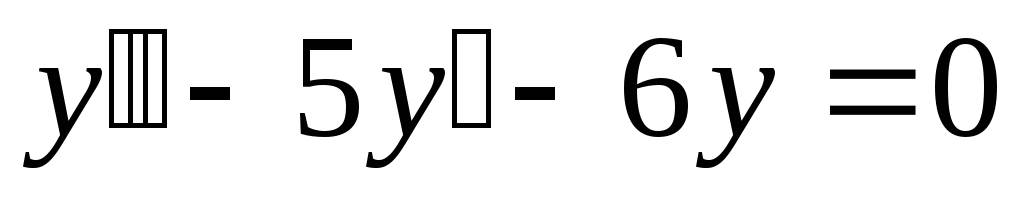 .
Составляем характеристическое уравнение
.
Составляем характеристическое уравнение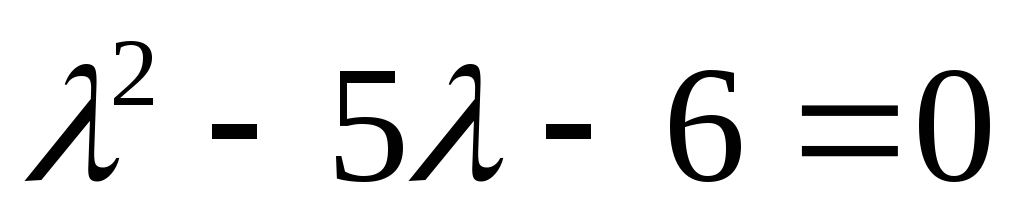 ,
откуда
,
откуда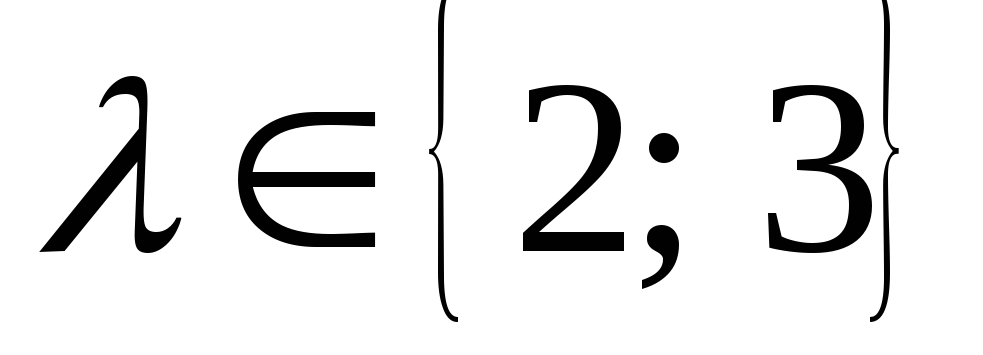 и
и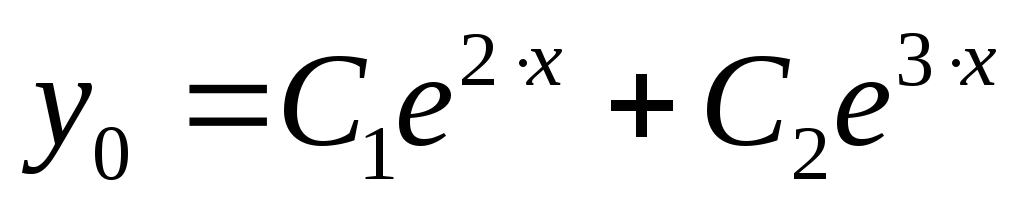 ;
;Неоднородное уравнение
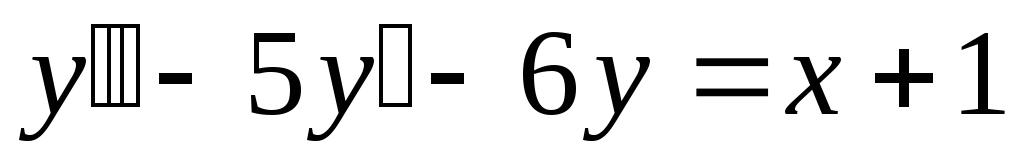 .
Частное решение: многочлен, наблюдающийся
в правой части
.
Частное решение: многочлен, наблюдающийся
в правой части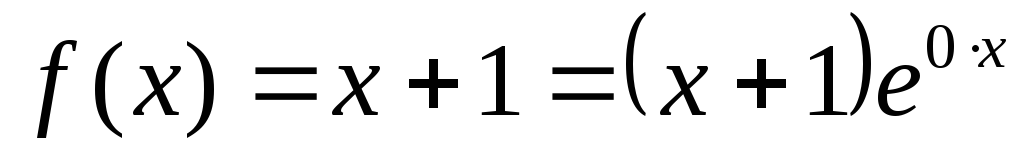 ,
записывается в общем виде
,
записывается в общем виде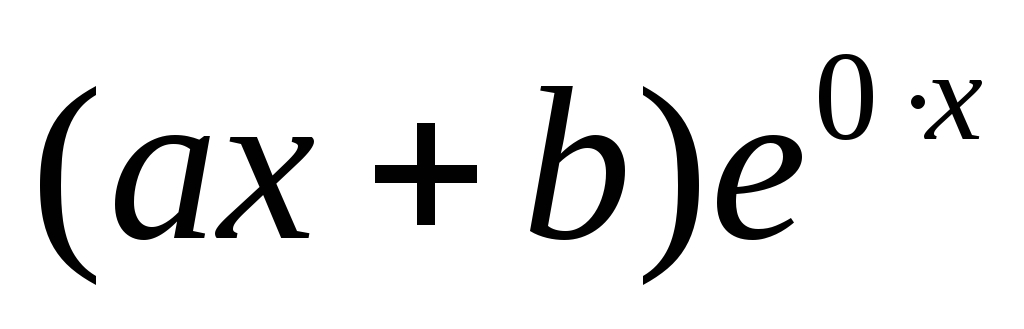 и полученная конструкция умножается
на
и полученная конструкция умножается
на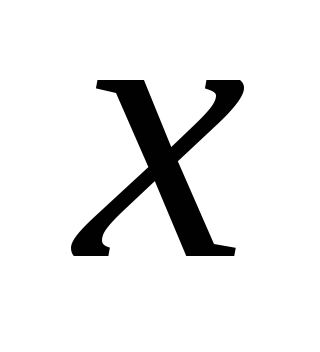 столько раз, сколько раз коэффициент
при
столько раз, сколько раз коэффициент
при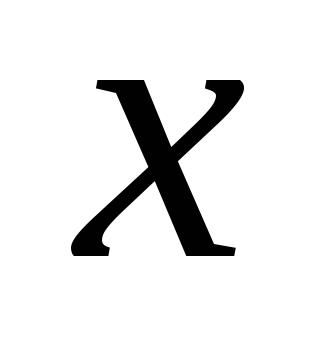 ,
стоящий в экспоненте правой части
,
стоящий в экспоненте правой части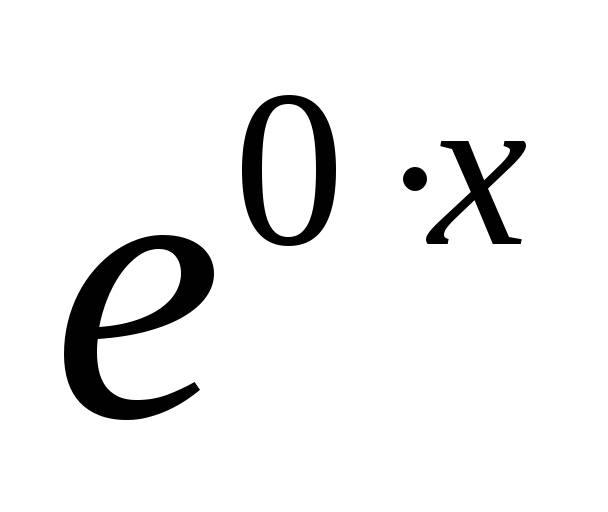 ,
присутствует в найденных ранее
,
присутствует в найденных ранее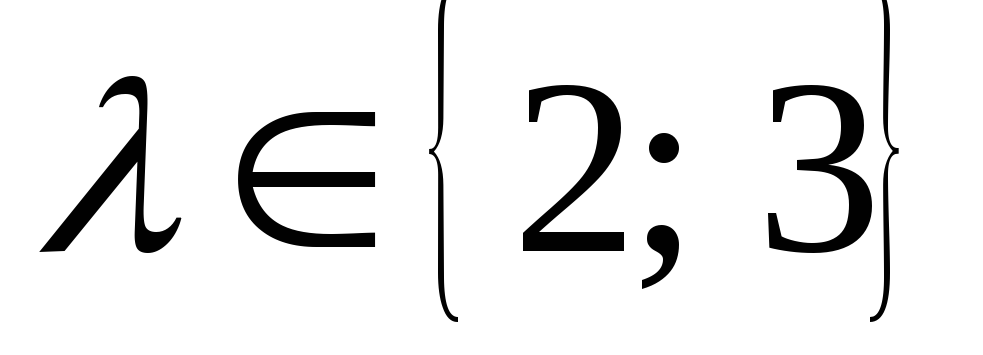 .
В данном случае
.
В данном случае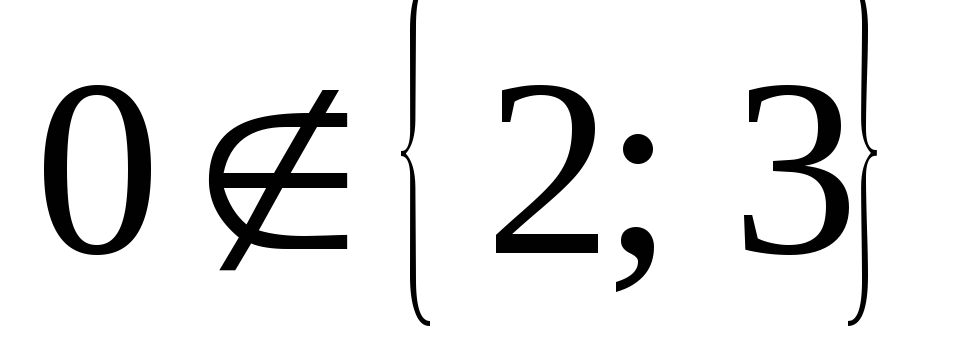 .
т.е. на
.
т.е. на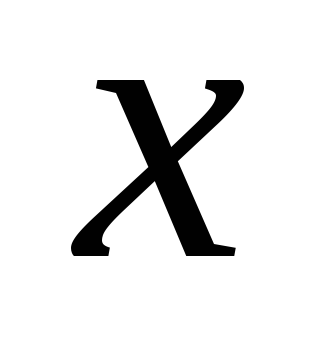 домножать не требуется.
домножать не требуется.
В итоге
![]() .
Обозначение констант не играет роли и,
сравнивая с вариантами ответов, приходим
к заключению, что истинен третий.
.
Обозначение констант не играет роли и,
сравнивая с вариантами ответов, приходим
к заключению, что истинен третий.
М30.
Интегральная кривая дифференциального
уравнения I
порядка
![]() ,
удовлетворяющая условию
,
удовлетворяющая условию![]() ,
имеет вид
,
имеет вид
Решение: Сначала
выясним какие варианты удовлетворяют
начальному условию. Для этого подставим
в каждое уравнение
![]() и
и![]() .
Верными окзываются первый и третий
варианты ответов. Далее заменим
.
Верными окзываются первый и третий
варианты ответов. Далее заменим![]() и, после разнесения переменных,
проинтегрируем:
и, после разнесения переменных,
проинтегрируем:![]() .
Уже после вычисления левого интеграла
.
Уже после вычисления левого интеграла![]() становится
ясно, что третий вариант ответа не может
быть верным.
становится
ясно, что третий вариант ответа не может
быть верным.
М31.
Семейству интегральных кривых
![]() соответствует линейное однородное
дифференциальное уравнениеII
порядка
соответствует линейное однородное
дифференциальное уравнениеII
порядка
Решение: составим
характеристические уравнения для
предложенных ответов (за исключением
первого, т.к. данное уравнение не является
однородным из-за свободного слагаемого
![]() ):
):
![]()
![]() верно.
верно.
![]()
![]()
![]()
![]()