Аналитическая геометрия

A1. Расстояние между точками иравно 5 приравном

• 10

• 4

• 6

• 1

Решение: . Далее из уравнения. Верным ответом из предъявленного выбора является.

А2. Установите соответствие между уравнением плоскости и её положением в пространстве:

○ ○ параллельна оси

○ ○ параллельна оси

○ ○ параллельна оси

○ ○ проходит через ось

○ проходит через начало координат

Решение: Вектор нормали (перпендикуляра) плоскости ортогонален направляющему векторуоси(нетрудно убедиться, что скалярное произведение). Следовательно, осьпараллельна данной плоскости.

Аналогично для плоскости имеем, следовательно плоскость параллельна оси, а плоскостьсоответственно оси.

Последняя плоскость с нормальным векторомне ортогональна осям. Проверим оставшиеся соответствия:

а) если бы плоскость проходила через ось , то её уравнению удовлетворяла бы точкапри всех значениях. Подставляя в уравнение плоскости, получим:, что выполняется лишь при одном. Плоскость не проходит через ось.

b) для выяснения случая «проходит ли плоскость через начало координат», подставим точку в уравнение:- верно. Следовательно, плоскость проходит через начало координат.

А3. Установите соответствие между уравнениями плоскости и точками, которые лежат в этих плоскостях:

○ ○

○ ○

○ ○

○ ○

○

Решение: Подставляем каждую точку в уравнения плоскостей пока не определим все тождества:

Точка удовлетворяет уравнению первой плоскости; точка- третьей;- не принадлежит ни одной плоскости;- удовлетворяет уравнению четвертой плоскости, а- принадлежит второй.

А4. В прямоугольной системе координат на плоскости заданы точки и, причем. Сравнивая расстояния от этих точек до начала координат, получаем

• 

• 

• 

• 

Решение: Вычисление расстояний дает

,

.

Следовательно, верным ответом является .

А5. Если уравнение гиперболы имеет вид , то длина её действительной полуоси равна

• 3

• 4

• 16

• 9

Решение: Каноническое уравнение гиперболы имеет вид , гдевещественная, амнимая полуоси. Из уравнения получаем.

Замечание. В случае эллипса ,большая ималая полуоси, причем.

А6. Расстояние от точки до плоскостиравно

• 

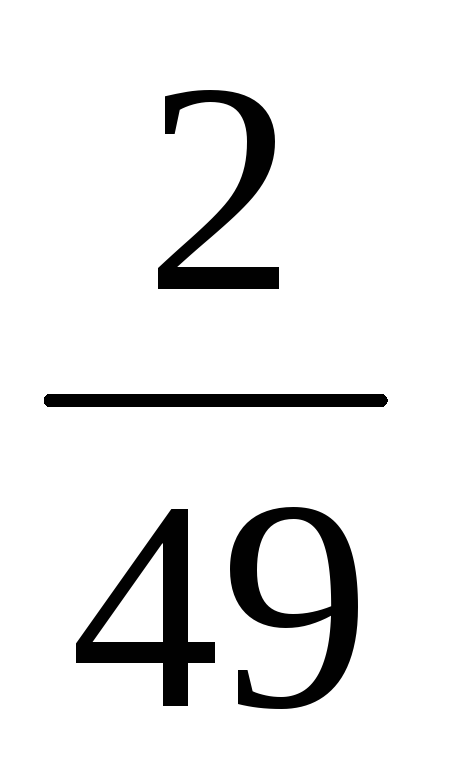
• 7

• 2

• 

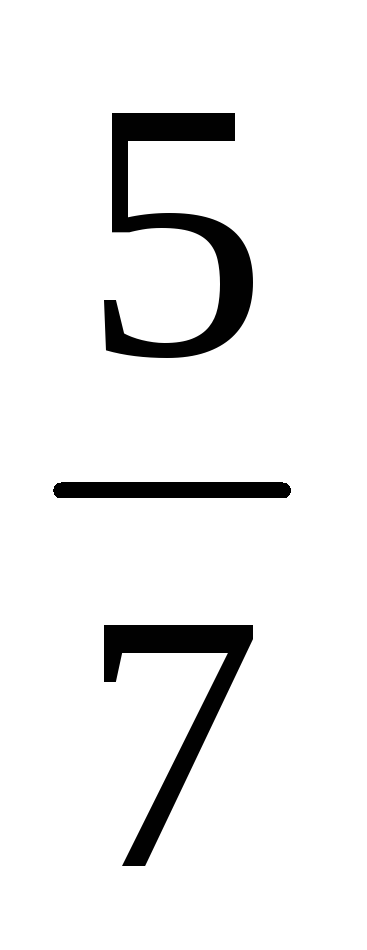
Решение: Вектор нормали к плоскости , его длина.

Тогда для нахождения расстояния от точки до плоскостидостаточно подставить координаты точки в левую часть уравнения плоскости и разделить результат на длину вектора нормали:

.

Замечание. Формула верна и для случая нахождения расстояния от точки до прямой на плоскости. В этом случае формула выглядит проще:

пусть , тогда.

А7. Если ,,. Тогда угол между векторамииравен

• 0

• 

• 

• 

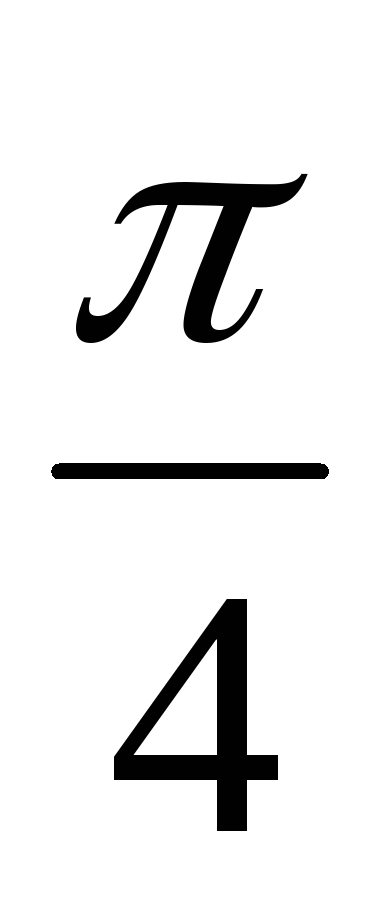
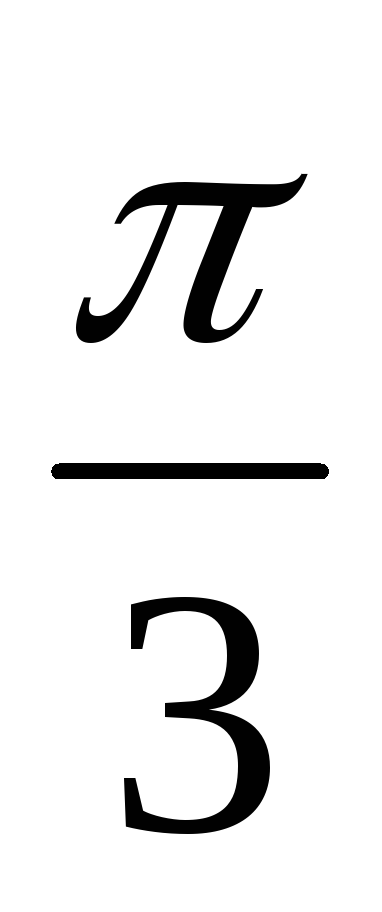
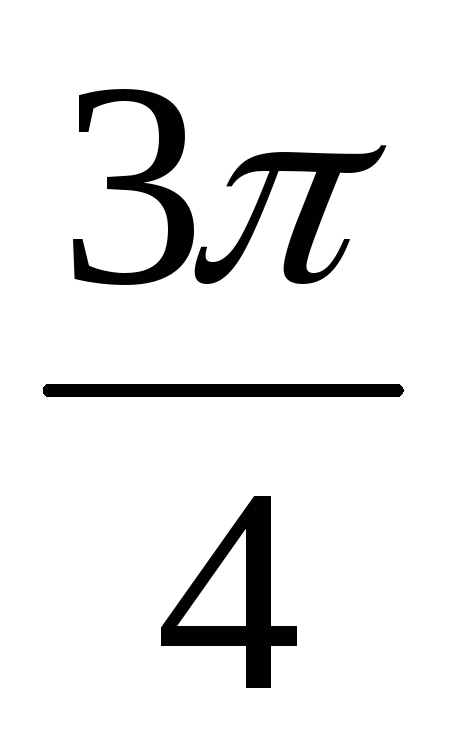
Решение: , что отвечает.

A8. Норма вектора в пространстверавна

• 14

• 100

• 10

• -10

Решение: В пространстве векторзадан путём разложения по каноническому базису:, т.е. можно записать. Тогда норма (длина) вектора.

А9. Треугольник задан вершинами и. Тогда площадь треугольника равна

• 1

• 3

• 5

• 7

Решение: Образуем векторы и. Формула площади имеет вид:

.

А10. Треугольник задан вершинами и. Тогда уголравен

• 

• 

• 

• 

Решение: Образуем векторы сторон треугольника, исходящие из угла :и. Для полученных направляющих векторов вычислим косинус угла между ними по формуле, что соответствует.