
- •Федеральное государственное образовательное учреждение высшего профессионального образования
- •Гринева Наталья Владимировна Зададаев Сергей Алексеевич
- •125468, Ленинградский пр-т, 49
- •Содержание
- •Введение
- •Формы тестовых заданий
- •Решение тестовых заданий Линейная алгебра
- •Аналитическая геометрия
- •Математический анализ
- •Теория вероятностей
- •Математическая статистика
- •Экономические приложения
- •Смешанные типы
Введение
Пособие предназначено для эффективной подготовки студентов бакалавриата экономического профиля к тестированию на остаточные знания по дисциплине «математика». В руководстве представлены основные типы тестовых заданий, предъявляемые государственным стандартом математики.
Задания методически типизированы по темам дисциплины. В отдельные группы, также, вынесены задачи экономических приложений и смешанные типы. Последняя группа особенно актуальна для студентов с особым математическим профилем: факультет «Математические методы в экономике и анализ риска» и «Антикризисное управление».
В качестве самопроверки уровня подготовки, настоятельно рекомендуется прохождение тестирования на сайте Росаккредагенства Рособрнадзора министерства образования и науки www.fepo.ru.
Формы тестовых заданий
К основным формам тестовых заданий относятся следующие ниже типы.
Задания с выбором ответа
Данная форма подразделяется на два подтипа: выбор единственного варианта ответа и выбор нескольких верных утверждений. В первом случае используются круглые маркеры вариантов, допускающие лишь единственный выбор:
В случае множественного ответа маркеры выглядят в виде квадратов:
Задания с введением ответа
 В
таких тестовых заданиях варианты ответа
не приводятся. Полученный ответ необходимо
внести в специальное поле ,
В
таких тестовых заданиях варианты ответа
не приводятся. Полученный ответ необходимо
внести в специальное поле ,
согласно указанному в задании формату:
Вычислить
![]() .
В ответе указать значение с точностью
трех знаков после запятой. Ответ: 1.414
.
В ответе указать значение с точностью
трех знаков после запятой. Ответ: 1.414
Задания на соответствия
Смыслом данного типа тестовых заданий является нахождение соответствующих пар эквивалентных друг другу вариантов ответа:
ц
 елое
число
елое
число![]()
р
 ациональное
число
ациональное
число![]()
и
 ррациональное
число
ррациональное
число![]()

комплексное число
Задания на упорядочивание
В подобных заданиях требуется упорядочить варианты ответов, согласно условию: расположите векторы по убыванию длины

![]()

![]()

![]()
Решение тестовых заданий Линейная алгебра
L1.
Определитель
 равен
равен
-1
-5
5
-1
Решение: I способ (метод треугольников):
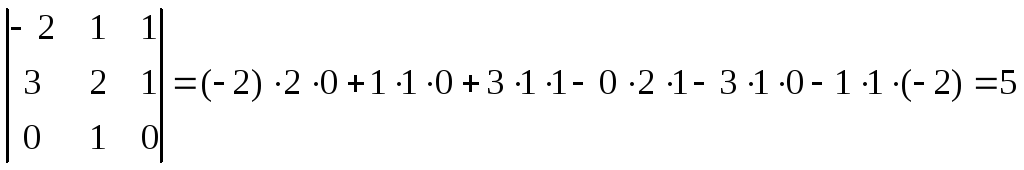
II способ (разложение по строке/столбцу): Выберем третью строку:
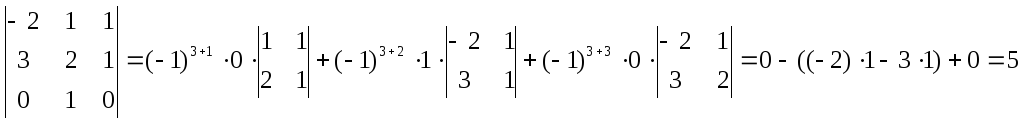
L2.
Если
![]() и
и![]() ,
тогда матрица
,
тогда матрица![]() имеет вид
имеет вид
Решение:
![]() .
.
L3.
Алгебраическое дополнение элемента
![]() определителя
определителя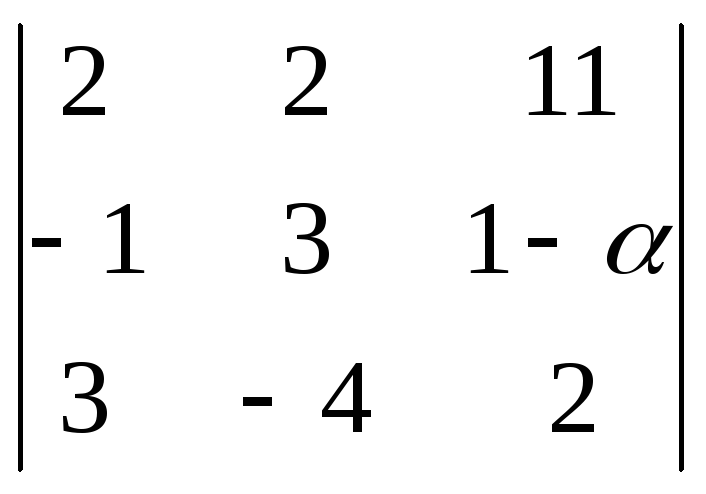 равно 1 при
равно 1 при![]() равном
равном
7
3
-4
6
Решение: Вычеркиваем
строку и столбец матрицы, содержащий
элемент
![]() ,
и записываем алгебраическое дополнение
,
и записываем алгебраическое дополнение
![]() .
.
Из уравнения
![]() находим
находим![]() .
.
L4. Определитель основной матрицы системы линейных уравнений
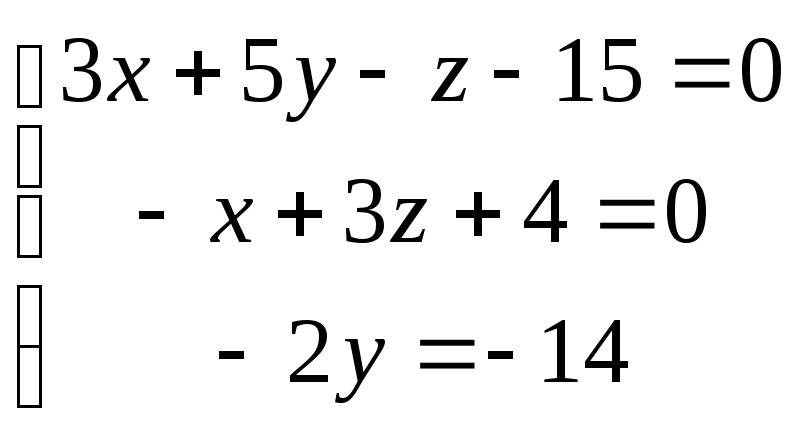
равен
0
16
22
26
Решение: Запишем систему уравнений в матричном виде:
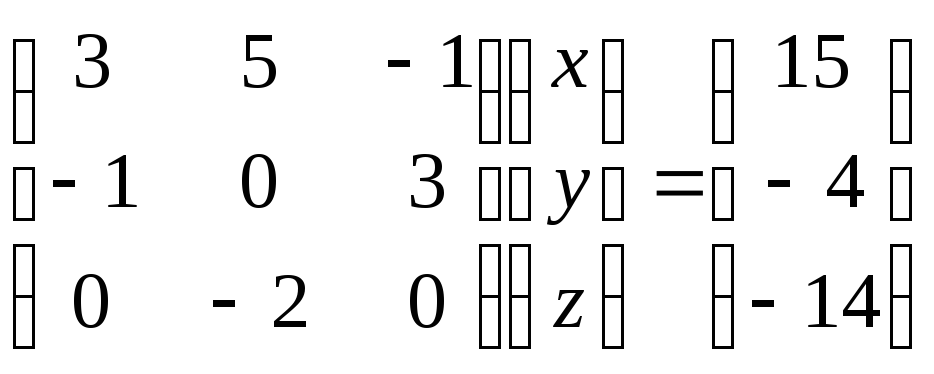 .
.
Находим определитель основной матрицы путем разложения по третьей строке (см. II способ примера L1.):
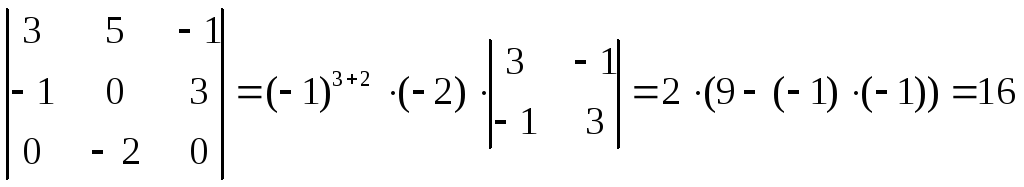 .
.
L5.
Определитель
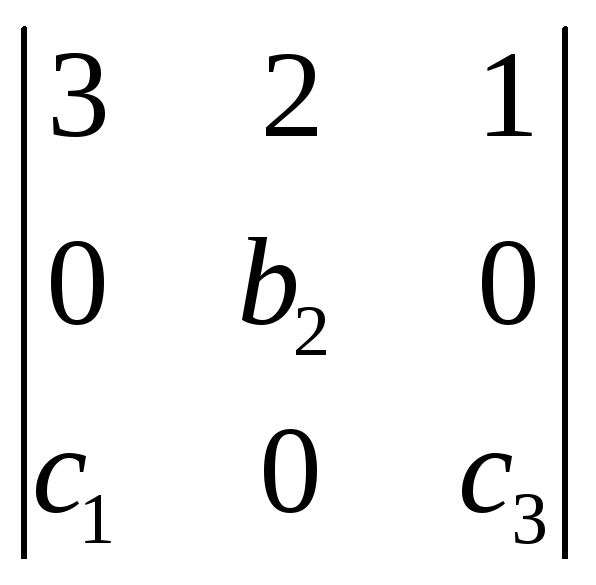 равен
равен
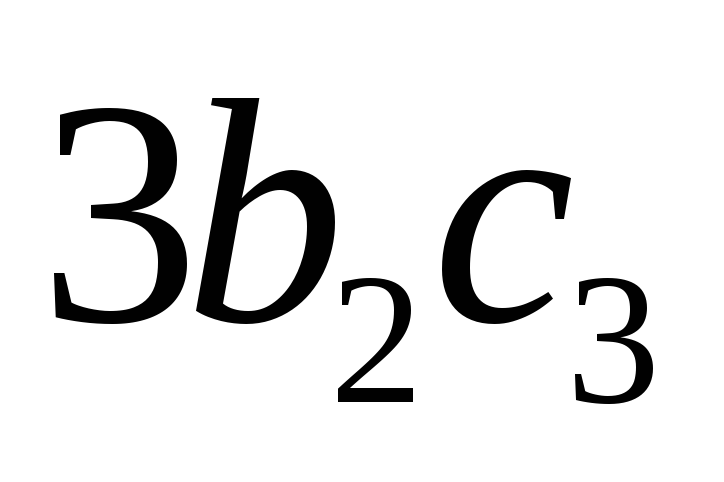
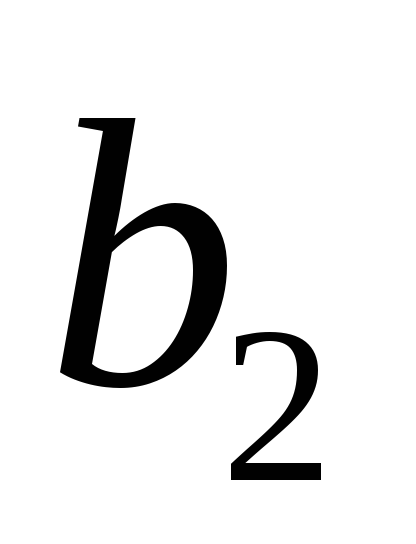
0

Решение: Разложим определитель по второй строке:
 .
.
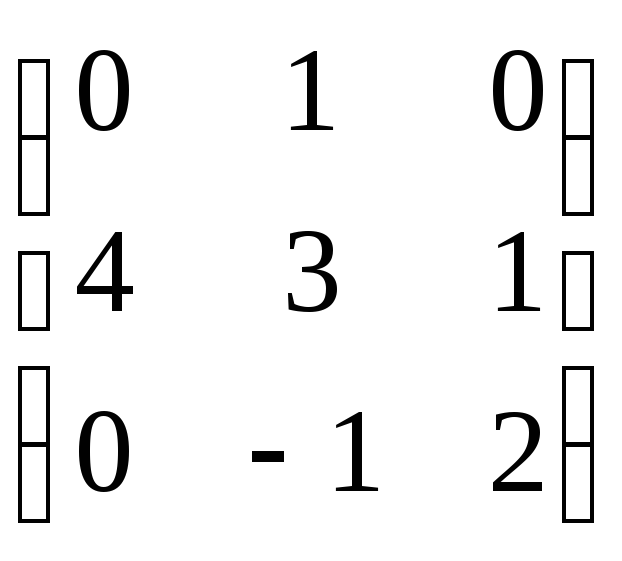
L6. Установите соответствие между матрицами и их рангами
○
 ○
1
○
1
○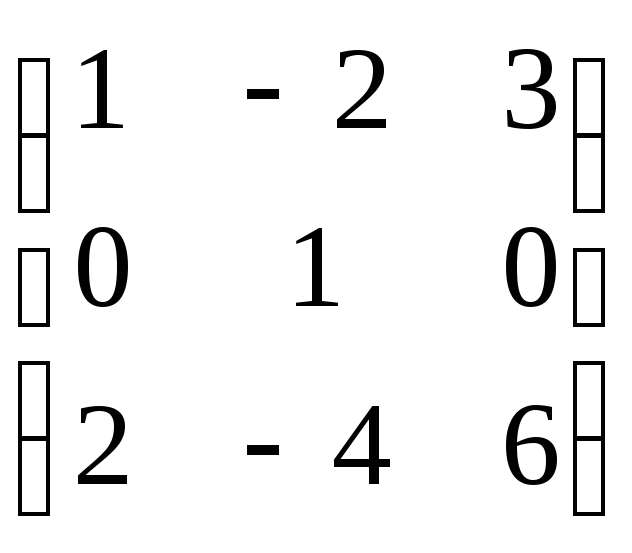 ○
4
○
4
○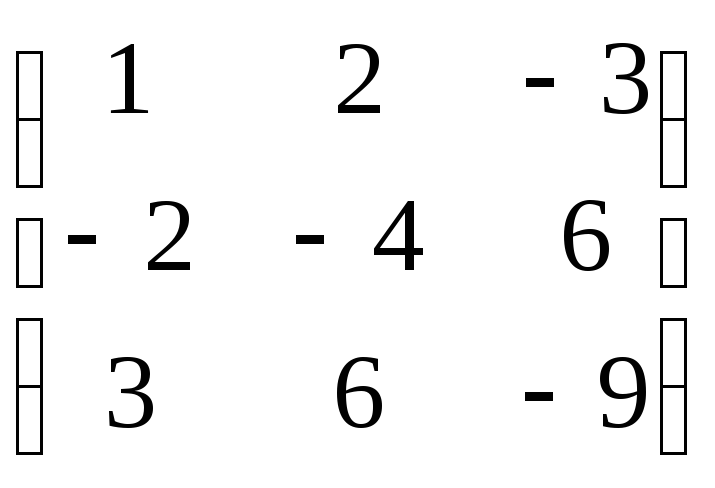 ○
5
○
5
○ ○
0
○
0
○ 2
○ 3
Решение: Рангом матрицы называется максимальное количество линейно независимых строк (столбцов). Вычислим ранги для каждой матрицы:
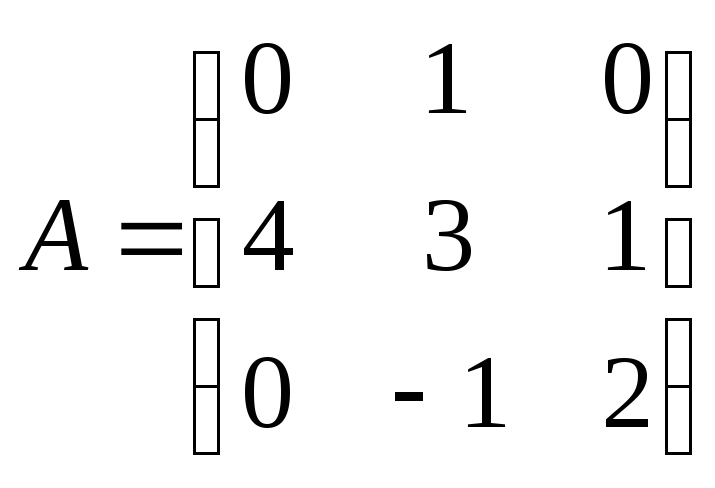 Если вычислить
определитель разложением по первой
строке, получим
Если вычислить
определитель разложением по первой
строке, получим
![]() .
Ненулевой определитель соответствует
линейно независимым строкам (столбцам),
т.е. заключаем, что ранг матрицы
.
Ненулевой определитель соответствует
линейно независимым строкам (столбцам),
т.е. заключаем, что ранг матрицы![]() равен 3.
равен 3.
 Если же в этом случае попробовать
вычислить определитель (по второй
строке), получим ноль. Это означает, что
строки матрицы линейно зависимы. Чтобы
определить максимальное количество
линейно независимых строк приведём
матрицу методом Гаусса к лестничному
виду:
Если же в этом случае попробовать
вычислить определитель (по второй
строке), получим ноль. Это означает, что
строки матрицы линейно зависимы. Чтобы
определить максимальное количество
линейно независимых строк приведём
матрицу методом Гаусса к лестничному
виду:
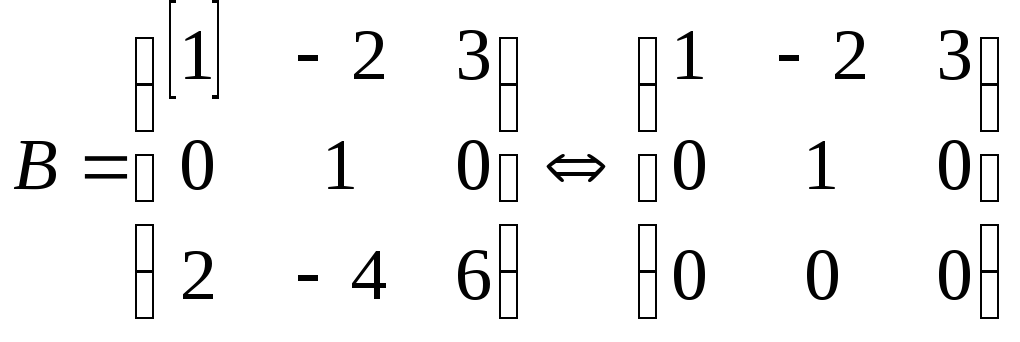 .
Отбрасывая третью строку как нулевую,
получаем, что ранг матрицы равен 2.
.
Отбрасывая третью строку как нулевую,
получаем, что ранг матрицы равен 2.
 .
Поступая аналогично приходим к
.
Поступая аналогично приходим к
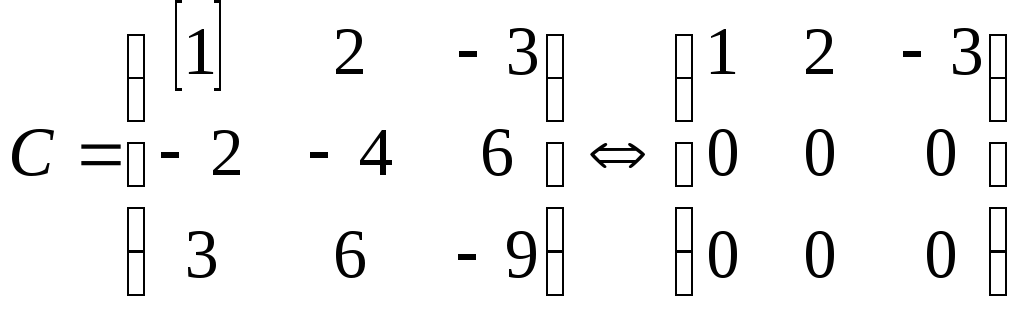 .
Остается лишь подсчитать количество
ненулевых строк – ранг равен 1.
.
Остается лишь подсчитать количество
ненулевых строк – ранг равен 1.
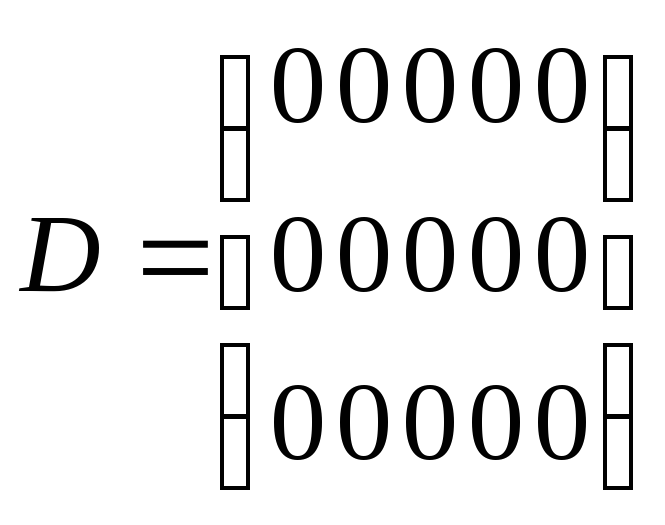 .
Ранг нулевой матрицы по определению
равен 0.
.
Ранг нулевой матрицы по определению
равен 0.
L7.
Матрица
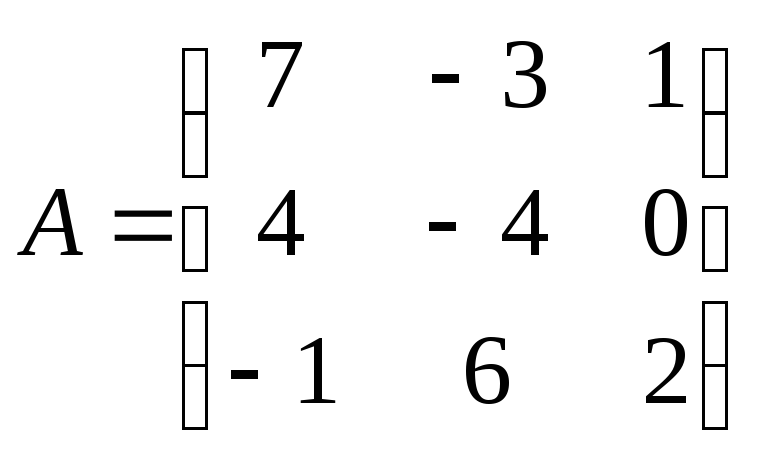 .
Тогда сумма элементов, расположенных
на главной диагонали, равна
.
Тогда сумма элементов, расположенных
на главной диагонали, равна
4
5
-4
10
Решение:
![]() .
.
L8. Разность между числом свободных и базисных переменных системы уравнений


равна
Решение: Запишем расширенную матрицу системы:
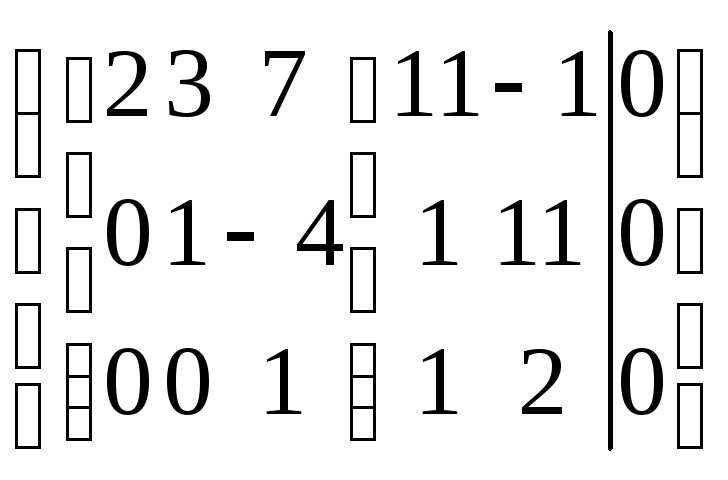 .
.
Основная матрица
системы оказывается уже приведённой к
лестничному виду (выделено […]). Причем,
первые 3 переменные (столбцы) являются
базисными, а оставшиеся 2 переменные
– свободными. Ответ:
![]() .
.
L9.
Дана система линейных уравнений
![]() .
Система не имеет решений при
.
Система не имеет решений при![]() равном
равном
0
-0.5
-2
2
Решение: Неоднородная
система уравнений несовместна, если в
лестничном виде образована противоречивая
строка
![]() .
Запишем расширенную матрицу:
.
Запишем расширенную матрицу:![]() .
Складывая строки, получим
.
Складывая строки, получим![]() .
Для образования противоречивой строки
необходимо
.
Для образования противоречивой строки
необходимо![]() .
Ответ:
.
Ответ:![]() .
.
Замечание: В данном
случае квадратной неоднородной системы
можно было бы приравнять определитель
основной матрицы к нулю:
![]() .
.
L10.
Квадратичная
форма
![]() является положительно определённой
при
является положительно определённой
при![]() равном
равном
2
1
-5
0
Решение: Составим
матрицу квадратичной формы
![]() .
Согласно критерию Сильвестра для
положительной знакоопределенности
необходимо и достаточно
.
Согласно критерию Сильвестра для
положительной знакоопределенности
необходимо и достаточно .
Подставляя поочередно предложенные
ответы, приходим к выводу, что верным
является лишь
.
Подставляя поочередно предложенные
ответы, приходим к выводу, что верным
является лишь![]() .
.
Замечание. Для
отрицательной знакоопределенности
было бы
![]() .
.
L11. В системе уравнений
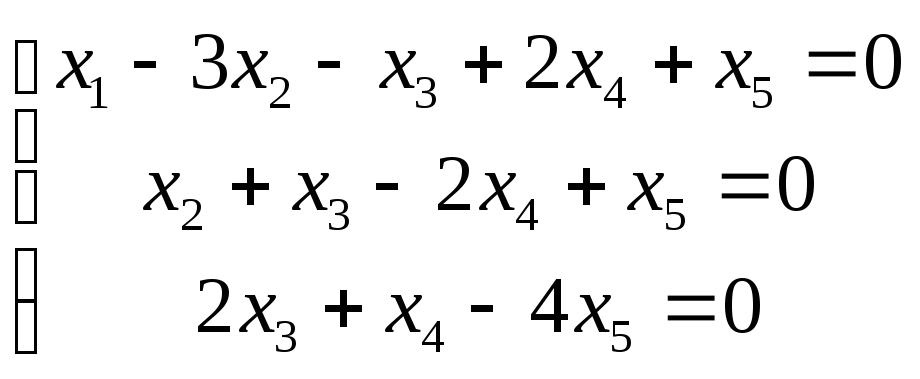
независимыми (свободными) переменными можно считать
Решение: Запишем расширенную матрицу системы:
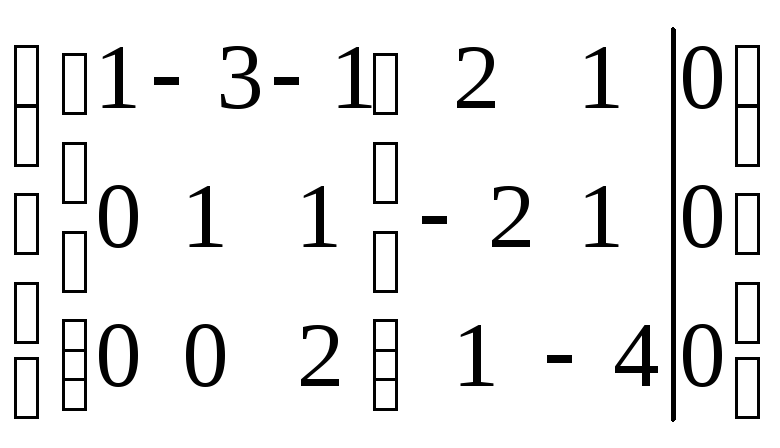 .
.
Основная матрица системы оказывается уже приведённой к лестничному виду (выделено […]). Причем, первые 3 переменные (столбцы) являются базисными, а оставшиеся 2 переменные – свободными. Количество базисных и свободных переменных не зависит от самих переменных. Таким образом, из предложенных вариантов ответов подходит лишь первый, т.к. в оставшихся количество свободных переменных не равно 2.
