
Пусть заданы векторы в прямоугольной системе координат
 тогда
тогда

Скалярное произведение векторов.
Определение.
Скалярным произведением векторов
 и
и называется число, равное произведению
длин этих сторон на косинус угла между
ними.
называется число, равное произведению
длин этих сторон на косинус угла между
ними.


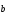 =
=
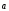
 cos
cos
Свойства скалярного произведения:

 =
=
 2;
2;
 =
0, если
=
0, если

 или
или
 =
0 или
=
0 или = 0.
= 0.
 =
=

 ;
; (
( +
+ )
=
)
=

 +
+
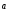
 ;
;(m
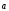 )
)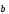 =
=
 (m
(m )
= m(
)
= m(
 );
);
Если
рассматривать векторы
 в
декартовой прямоугольной системе
координат, то
в
декартовой прямоугольной системе
координат, то


 =
xa
xb
+ ya
yb
+ za
zb;
=
xa
xb
+ ya
yb
+ za
zb;
Используя
полученные равенства, получаем формулу
для вычисления угла между векторами:
 ;
;
Пример.
Найти (5 + 3
+ 3 )(2
)(2 -
- ),
если
),
если
10
 -
5
-
5
 +
6
+
6
 -
3
-
3
 = 10
= 10 ,
,
т.к.
 .
.
Пример.
Найти угол между векторами
 и
и ,
если
,
если
 .
.
Т.е.
 = (1, 2, 3),
= (1, 2, 3), =
(6, 4, -2)
=
(6, 4, -2)

 =
6 + 8 – 6 = 8:
=
6 + 8 – 6 = 8:
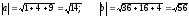 .
.
cos
=

Пример.
Найти скалярное произведение (3 - 2
- 2 )(5
)(5 - 6
- 6 ),
если
),
если
15
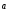 -
18
-
18
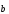 -
10
-
10
 +
12
+
12
 = 15
= 15
+ 1236 = 240 – 336 + 432 = 672 – 336 = 336.
Пример.
Найти угол между векторами
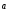 и
и ,
если
,
если
 .
.
Т.е.
 = (3, 4, 5),
= (3, 4, 5), =
(4, 5, -3)
=
(4, 5, -3)

 =
12 + 20 - 15 =17 :
=
12 + 20 - 15 =17 :
 .
.
cos
=

Пример.
При каком m
векторы
 и
и перпендикулярны.
перпендикулярны.
 =
(m,
1, 0);
=
(m,
1, 0);
 =
(3, -3, -4)
=
(3, -3, -4)
 .
.
Пример.
Найти скалярное произведение векторов
 и
и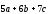 ,
если
,
если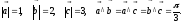
(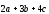 )(
)( )
=
)
=

 =
10 +
=
10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
Пример. Дан треугольник АВС. где А(1, 2); В(0, 3); С(-2, -1). Найти
периметр его и угол А.
Решение
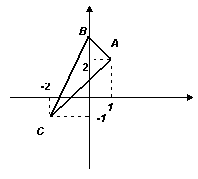
Обозначим
векторы
 .
Используя скалярное произведение,
найдем
.
Используя скалярное произведение,
найдем
 .
Координаты вектораā
находим, вычитая из координат его
конца - точки С, соответствующие
координаты начала его точки А.
.
Координаты вектораā
находим, вычитая из координат его
конца - точки С, соответствующие
координаты начала его точки А.

Аналогично,
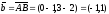
Найдем 
Таким
образом,

Чтобы найти периметр ΔАВС, надо найти длины всех его сторон:

Итак, периметр ΔАВС равен

Векторное произведение векторов.
Векторным
произведением векторов
 называют такой вектор
называют такой вектор ,
что
,
что
1)

то есть длина вектора равна площади параллелограмма, построенного на этих векторах;
2)
вектор
 перпендикулярен плоскости, в которой
лежат векторы
перпендикулярен плоскости, в которой
лежат векторы ;
;
3)
векторы
 образуют
правую - тройку, то есть вектор
образуют
правую - тройку, то есть вектор
 направлен
так, что, если смотреть с конца вектора
направлен
так, что, если смотреть с конца вектора
 ,
то кратчайший поворот от
,
то кратчайший поворот от совершается
против часовой стрелки.
совершается
против часовой стрелки.
Векторное
произведение обозначается
 или
или
 .
.

Свойства векторного произведения:
1.

2.
 ,λ
- скаляр;
,λ
- скаляр;
3.

Пример. Найти векторное произведение ортов (базисных векторов) i, j, k.
Решение
 ,
так как
,
так как

аналогично
 ;
;
Согласно определению:


Векторное произведение в координатной форме.
Пусть
известны координаты векторов
 ,
то есть
,
то есть

Используя свойства векторного произведения, найдем:

Выражения в скобках можно записать с помощью определителей второго порядка (проверьте), то есть:

правую часть последнего выражения можно записать с помощью определителя третьего порядка:

Эта формула является удобной записью векторного произведения в координатах.
Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Из
определения векторного произведения
следует, что площадь параллелограмма,
построенного на векторах
 ,
равна модулю векторного произведения:
,
равна модулю векторного произведения:

в
частности, площадь
треугольника

Одним
из физических приложений векторного
произведения является нахождение
момента силы,
возникающего при вращении твердого
тела, закрепленного в некоторой точке
А, под действием силы
 ,
приложенной в точке В:
,
приложенной в точке В:

Пример. Найти площадь треугольника АВС, где А (-2, 1, 0);
В (3,4, 8); С (-1,3,6).
Решение
Площадь
треугольника, построенного на векторах
 и
и ,
равна
,
равна

Найдем координаты векторов:
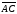 =(-1+2;
3-1; б-0)=(1,2,6)
=(-1+2;
3-1; б-0)=(1,2,6)
 =(3-(-2);
4-1; 8-0)=(5, 3, 8)
=(3-(-2);
4-1; 8-0)=(5, 3, 8)
их векторное произведение равно:

Итак,
 или
или
Пример.
Найти векторное произведение векторов
 и
и
 .
.
 =
(2, 5, 1);
=
(2, 5, 1);
 =
(1, 2, -3)
=
(1, 2, -3)
 .
.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),
С(0, 1, 0).



 (ед2).
(ед2).
Пример.
Доказать, что векторы
 ,
, и
и компланарны.
компланарны.
 ,
т.к. векторы линейно зависимы, то они
компланарны.
,
т.к. векторы линейно зависимы, то они
компланарны.
Пример.
Найти площадь параллелограмма,
построенного на векторах
 ,
если
,
если

 (ед2).
(ед2).
