Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Брестский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матемVM_Санюкевич А.В._ч

.1.pdf

Скачиваний:

Добавлен:

01.03.2016

Размер:

575.29 Кб

Скачать

☆

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

12. 1)

= 5,19 ;

= 2,63 .

0,85637 ; δ =0,21% .

а)

X =

, a = 315,6(±0,05) , b =72,5(±0,03) , c = 53,8(±0,04) ;

б) X =

(a +b) m3

c −d

, a =18,5(±0,03) , b = 5,6(±0,02), c = 26,3(±0,01),

m = 3,42(±0,003) , d =14,782(±0,006) .

M =

(a +b)h3

(a +b)h

, a =6,44 , b =

5,323,

h =15,44 .

13. 1)

= 5,56 ;

=0,764 .

15,873 ; δ =0,42% .

а)

X =

a = 4,632(±0,003) , b = 23,3(±0,04) , c =11,3(±0,06) ;

б)

X =

(a +b) m , a = 3,236(±0,002), b =15,8(±0,03), c =12,415(±0,003) ,

(c −d )2

m=0,64(±0,004) , d =7,18(±0,006) .

4)N = (a +b)2 + (a2 +b2 )h , a =0,834 , b =0,3523, h =0,74 . 2h 5

14. 1)

= 3,60 ;

=0,318 .

0,3945 ; δ =0,16%.

a2b

а)

X =

a =1,

245(±0,001) , b =0,121(±0,0002), c = 2,34(±0,003) ;

б)

X =

(a +b)

m ,

a =17,41(±0,01) , b =1,27(±0,002), c = 342,3(±0,04),

c −d

m =0,71(±0,003) ,

d =11,7(±0,1) .

= h S

, a = 5,71,

A = 32,17 , S = 51,7 , h = 2,42.

15. 1)

= 4,243;

17 =1,545 .

24,3618 ; δ =0,22% .

ab3

а)

X =

a =0,142(±0,0003) ,

b =1,71(±0,002) , c = 3,727(±0,001) ;

б)

X =

−b)

c ,

a =15,71(±0,005) , b = 3,28(±0,02) , c =7,2(±0,01),

m + n

m=13,752(±0,001) , n = 33,7(±0,03).

4)S = h2 : a2 +4ab +2 b2 , a = 32,47 , b =11,42, h =17,8 . 18 (a +b)

16. 1)				=6,16 ; 5				=1,667 .		2) 3,7542 ; δ =0,32% .
16. 1)		38		=6,16 ; 5				=1,667 .		2) 3,7542 ; δ =0,32% .
			X = ab				3
3)	а)		X = ab				, a =0,1756(±0,0001) ,			b = 3,71(±0,03), c =0,285(±0,0002);
					c2		a +b
	б)		X =				a +b		, a =12,751(±0,001) , b = 3,7(±0,02) , c = 23,76(±0,003) ,

						(c −d)m
						(c −d)m

m=1,7(±0,01) , d = 8,12(±0,004) .

4)V = 61πh(3a2 + h2 ) , a =7,751, h = 3,35 .

17. 1)

= 5,48 ;

= 3,77 .

83,736 ; δ =0,085%.

π2

а) V

Dd 2 , π = 3,14 , D =72(±0,3), d = 3,274(±0,002) ;

б) S =

−d 4

D = 41,4(±0,2) ,

d = 31,75(±0,003), π = 3,14 .

a = c

γ 2

c =7,834 , β =0,21, γ = 3,71.

18. 1)

= 2,64 ; 13

=1,857 .

2,8867 ; δ =0,43% .

m2n

а) Y

m = 2,348(±0,002) , n = 4,37(±0,004), c =0,235(±0,0003) ;

б) X = a −b m , a = 8,357(±0,003) , b = 2,48(±0,004), c + d

c=1,315(±0,0004), m = 3,17(±0,01), d = 2,4(±0,02) .

4)V = 151 πh(2D2 + Dd +0,75d 2 ), h = 84,2 , D = 28,3 , d = 42,08 .

19. 1)

= 3,46 ; 19

=1,58 .

0,096835 ; δ =0,32% .

а)

X =

, c =0,8345(±0,0004), d =13,8(±0,03) , b =1,84(±0,006) ;

б)

X =

a −b

, a = 9,37(±0,004) , b = 3,108(±0,0003) , m =0,46(±0,002) ,

m(n −a)

n =15,2(±0,04).

S =

, где

p = a +b +c ,

a =10,5 , b = 34,18 ,

p( p −a)( p −b)( p −c)

c = 27,327 .

20. 1)

= 5,91;

= 4,64 .

0,66385 ; δ =0,34% .

Qe3

а) f =

Q = 38,5(±0,01), e = 3,35(±0,02) ,

E =0,734(±0,001) ;

48E

1)2 (x + y)

б) Q =

(2n −

, n =1,1753(±0,0002),

x = 5,8(±0,01) ,

x − y

y =0,65(±0,02).

γ = αb − βa

−

β (ab − βα)

, a = 234,36 , b = 81,26 , α =7,31, β =0,0761.

b2 (b + β)

21. 1)

= 4,69 ;

= 2,57 .

46,453 ; δ =0,15%.

а) X =

, a =7,27(±0,01) , b = 5,205(±0,002) , c = 87,32(±0,03) ;

3 c

б) X =

(a +b) c 2

a = 2,13(±0,01) , b = 22,16(±0,03), c =6,3(±0,04) ,

−n

m =16,825(±0,004) , n = 8,13(±0,002) .

S =

+4ab +b2

, a = 5,813, b =1,315, h = 2,56 .

(a +b)2

22. 1)

= 4,12;

= 2,11.

5,8425 ; δ =0,23% .

а) X =

, a =186,7(±0,04) ,

b =66,6(±0,02) , c =72,3(±0,03) ;

б) X =

(a +b) m3

c −d

, a =11,8(±0,02), b =7,4(±0,03), c = 26,7(±0,03) ,

m= 5,82(±0,005), d =11,234(±0,004) .

4)M = (a +b)h3 + (a +b)h , a = 9,05 , b = 3,244 , h = 20,18 . 4 12

23. 1)				= 3,32 ;			16 = 2,28 .	2) 24,3872 ; δ =0,34% .
		11
							7
3)	а)		X =			ab	, a =7,312(±0,004), b =18,4(±0,03) , c = 20,2(±0,08);
						c

	б)		X =		(a +b) m , a = 4,523(±0,003), b =10,8(±0,02) , c = 9,318(±0,002) ,
					(c −d )2

m=0,85(±0,003) , d = 4,17(±0,004) .

4)N = (a +b)2 + (a2 +b2 )h , a =0,445 , b =0,4834 , h =0,87 . 2h 5

24. 1)

=7,94 ;

=1,54 .

45,7832 ; δ =0,18%.

a2b

а)

X =

a =

0,327(±0,005) , b = 3,147(±0,0001) , c =1,78(±0,001);

б)

X =

(a +b)

m , a = 32,37(±0,03) ,

b = 2,35(±0,001) , c =128,7(±0,02) ,

c −d

m =0,93(±0,001) ,

d = 27,3(±0,04).

= h S

1 +

, a =7,28 ,

A =11,71, S = 21,8 , h = 5,31.

25. 1)

=6,86 ;

=1,71.

72,354 ; δ =0,24% .

ab3

а)

X =

a =0,258(±0,0002) ,

b = 3,45(±0,001) , c =7,221(±0,003) ;

б)

X =

(a −b) c

, a =12,31(±0,004),

b =1,73(±0,03) , c = 3,7(±0,02) ,

m + n

m=17,428(±0,003) , n = 41,7(±0,01) .

4)S = h2 : a2 +4ab +2 b2 , a = 27,51, b = 21,78 , h = 32,5 .

18 (a +b)

26. 1)				=6,40 ; 6				=0,857 .		2) 46,7841; δ =0,32% .
26. 1)		41		=6,40 ; 6				=0,857 .		2) 46,7841; δ =0,32% .
			X = ab				7
3)	а)		X = ab				, a =0,2731(±0,0003),			b = 5,12(±0,02), c =0,374(±0,0001) ;
					c2		a +b
	б)		X =				a +b		, a = 31,456(±0,002), b =7,3(±0,01), c = 33,28(±0,003),

						(c −d)m
						(c −d)m

m= 5,8(±0,02) , d =6,71(±0,001) .

4)V = 61πh(3a2 + h2 ) , a = 5,441, h =6,17 .

27. 1)

= 9,33 ;

= 2,56 .

2) 23,7564 ; δ =0,44% .

π2

а) V =

Dd 2 , π = 3,14 , D = 31(±0,01) , d =7,345(±0,001);

б) S =

−d 4

, D = 52,6(±0,01) , d = 48,39(±0,001) , π = 3,14 .

a = c

2β

γ 2

, c = 4,539 ,

β =0,34 , γ = 5,93.

28. 1)

=6,48 ;

27 =0,872 .

2) 0,088748 ; δ =0,56% .

m2n

а) Y =

m = 3,804(±0,003) , n =

4,05(±0,003) , c =0,318(±0,0002);

б) X =

a −b

, a = 4,218(±0,001), b =1,57(±0,006) , c = 2,418(±0,004) ,

c + d

m= 2,32(±0,02) , d =1,8(±0,01) .

4)V = 151 πh(2D2 + Dd +0,75d 2 ), h = 45, D = 48,3 , d = 32,14 .

29. 1)

=7,61

; 7 = 2,33 .

3,87683 ; δ =0,33% .

а)

X =

, c =0,6384(±0,0002) ,

d = 32,7(±0,04), b = 4,88(±0,03) ;

, a =11,45(±0,01),

б)

X =

a −b

b = 4,431(±0,002) , m =0,75(±0,003) ,

m(n −a)

n =16,7(±0,05).

S =

, где p = a +b +c ,

a = 2,48 , b = 5,344 ,

p( p −a)( p −b)( p −c)

c =6,0218 .

30. 1)

=7,28

; 14 =0,823 .

23,3748 ; δ =0,27% .

Qe3

а)

, Q =17,3(±0,03) , e = 5,73(±0,01) ,

E =0,956(±0,004) ;

48E

б) Q =

(2n −1)2 (x

+ y)

, n = 4,5681(±0,0001) ,

x =6,3(±0,02),

x − y

y =0,42(±0,03) .

γ =

αb − βa −

β (ab − βα)

, a = 341,17 , b = 52,34 , α = 3,28 , β =0,0545 .

b2 (b + β)

ЛАБОРАТОРНАЯ РАБОТА № 2

МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ

Решение уравнений – алгебраических и трансцендентных – представляет собой одну из существенных задач прикладного анализа, потребность в которой возникает в самых разнообразных разделах физики, техники и естествознания.

Задача нахождения корня уравнения

		f (x) =0 ,	(2.1)
где f(x) – непрерывная функция, состоящая из двух этапов:
1)	отделение корня, т.е. определение числового промежутка, в котором
	содержится один корень уравнения;
2)	уточнение	значения корня путем построения	последовательности
	xk =ϕ(xk−1 )	( k =1,2,3,...) на основе соответствующего метода.

Для уточнения значения корня существуют различные итерационные методы.

2.1 Метод половинного деления

Сведения из теории

Отделение корня можно произвести графически. Для этого уравнение (2.1)

удобно представить в виде
g(x) = h(x)	(2.2)

и найти по чертежу абсциссу x0 точки пересечения графиков y=g(x) и y=h(x). Величину x0 определить с достаточной точностью графически невозможно.

Поэтому следует выбрать такой числовой промежуток [a;b], для которого заведомо выполняется неравенство a ≤ x0 ≤b .

Разные знаки функции при x=a и x=b
f (a) f (b) ≤0	(2.3)

свидетельствуют о наличии корня в промежутке [a;b].

Условие применимости метода половинного деления предполагает непрерывность функции f(x) на [a;b].

Уточнение значения корня производится путем построения сходящейся

последовательности
xk = (ak +bk ) / 2 , k =1,2,... .	(2.4)

За a1, b1 принимаем соответственно a, b.

Предполагая, что приближение xn (где n – фиксированное значение k) известно, для нахождения xn+1 выбираем последующие значения an+1, bn+1 в зависимости от знака произведения f (an ) f (xn ) .

Если f (an ) f (xn ) < 0, то bn+1 полагаем равным найденному значению xn и

an+1 – равным an, иначе bn+1 =bn , an+1 = xn .

На рис. 2.1 изображено

поведение последовательных приближений в случае f (a) <0 ,

f (b) >0 :

Рис. 2.1

Решение уравнения (2.1) считается найденным с точностью ε , если выполнится условие

		xk +1 − xk	<ε .		(2.5)
		xk +1 − xk	<ε .		(2.5)
Результаты вычислений следует поместить в таблицу 2.1:					Таблица 2.1
					Таблица 2.1
k – номер	ak	bk		xk	Знак
приближения	ak	bk		xk	f (ak ) f (xk )
приближения					f (ak ) f (xk )

Порядок выполнения работы

1)Определить промежуток [a;b], содержащий один корень уравнения (2.1), пользуясь приемом, описанным выше.

2)Проверить выполнение условия (2.3).

3)Вычисления по формуле (2.4) продолжать до выполнения условия (2.5).

Пример 2.1. Методом половинного деления найти значение корня уравнения 2 −lg x − x =0 с точностью ε =0,01.

Решение. 1) Данное уравнение представим в виде lg x = −x + 2. Построим графики функций y = lg x и y = −x + 2 .

y = −x + 2

y = lg x

Рис. 2.2

Из рис. 2.2 видно, что искомый корень лежит в промежутке [1;2]. 2) Проверим выполнение условия (2.3):

	f (1) = 2 −lg1 −1 =1 >0 ,								f (2) = 2 −lg 2 −2 ≈ −0,301 <0 .
Принимаем a1 =1,			b1 = 2 .
3)	Вычислим		x1 = (a1 +b1 ) / 2 =1,5.							Найдем	f (x1 ) = 2 −lg1,5 −1,5 ≈0,324 .
Тогда	f (a1 ) f (x1 ) >0 , следовательно
		a2 = x1 , b2 =b1				и x2 = (a2 +b2 ) / 2 = (1,5 + 2) / 2 =1,75 .
f (x2 ) =0,007 >0 ,			f (a2 ) f (x2 ) >0 , откуда
			a	= x		,	b =b ,		x	= a3 +b3	=1,875 .
			3	2			3	2	3	2
f (x3 ) = −0,148 <0 ,										2
f (x3 ) = −0,148 <0 ,			f (a3 ) f (x3 ) <0 , поэтому
	a	= a	, b = x ,		x		= a4 +b4 = 1,75 +1,875 =1,812 и т. д.
	4	3	4	3		4		2		2
								2		2

Значения последовательных приближений помещены в таблице 2.2: Таблица 2.2

k – номер	ak	bk	xk	Знак
приближения	ak	bk	xk	f (ak ) f (xk )
приближения				f (ak ) f (xk )
1	1	2	1,5	+
2	1,5	2	1,75	+
3	1,75	2	1,875	–
4	1,75	1,875	1,812	–
5	1,75	1,812	1,781	–
6	1,75	1,781	1,766	–
7	1,75	1,766	1,758	–

Так как		x7 − x6	= 1,758 −1,766 =0,008 <0,01, то условие (2.5) выполнено.
Поэтому x ≈1,76 .
					2.2 Метод итераций
					Сведения из теории
Уравнение (1) преобразуется к виду
						x =ϕ(x) .			(2.6)
Построение сходящейся последовательности проводится с помощью
соотношения					xk	=ϕ(xk −1 ) , k =1,2,3,...			(2.7)
					xk	=ϕ(xk −1 ) , k =1,2,3,...			(2.7)
исходя из начального приближения x0 [a;b].
Достаточным условием сходимости метода итераций является выполнение
неравенства						′
						′			(2.8)
						ϕ (x) <1			(2.8)
на промежутке [a;b].
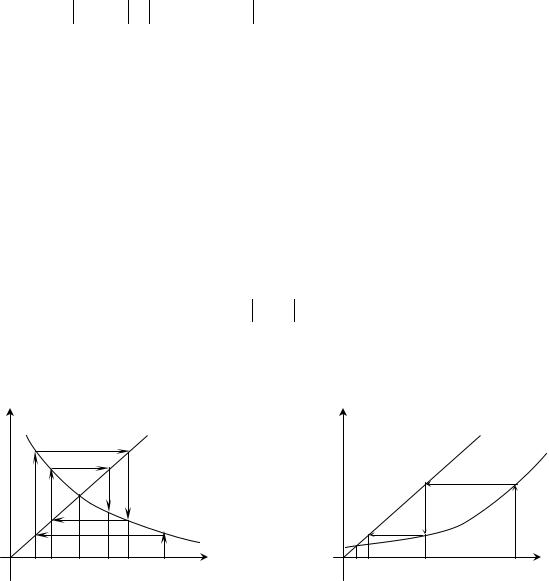
На	рис. 2.3 изображено					поведение последовательных			приближений	в
		′				′
случаях: а) −1 <ϕ (x) <0 ; б) 0 <ϕ (x) <1.
y						y
				y = x				y = x	y =ϕ (x)
				y =ϕ (x)
0	x1 x3	x	x	x	x	0	x2	x	x
0		4	2	0	x	0		1	0 x
		a)						б)

Рис. 2.3 Критерием окончания итераций служит выполнение условия (2.5).

Порядок выполнения работы

1) Методом половинного деления (п.п. 1, 2) выбрать начальное приближение.

2)Представить уравнение (2.1) в виде (2.6).

3)Проверить выполнение условия (2.8).

4)Продолжить вычисления по формуле (2.7) до выполнения условия (2.5).

Пример 2.2. Методом итерации найти значение корня уравнения 2 −lg x − x =0 с точностью ε =0,01.

Решение. 1) Отделение корня и проверка выполнения условия (2.3) для данного уравнения произведены в примере 2.1. Пусть x0 =1.

Запишем исходное уравнение в виде x = 2 −lg x , т.к. ϕ(x) = 2 −lg x .

′

lge

как

′

<1, то последовательность

ϕ (x)

= − x . Так

ϕ (1)

ϕ (2)

xk = 2 −lg xk−1 будет сходиться в промежутке [1;2].

Строим последовательные приближения

x1 = 2 −lg x0 = 2 −lg1 = 2 , x2

= 2 −lg x1 = 2 −lg 2 =1,699 ,

x3 = 2

−lg x2 = 2 −lg1,699 =1,770 ,

x4 = 2 −lg x3 = 2 −lg1,770 =1,753 ,

= 2 −lg x4 = 2 −lg1,753 =1,757 .

x≈1,76 , т.к. x5 − x4 =0,004 <0,01.

2.3Метод хорд (метод пропорциональных частей)

Сведения из теории

Условия сходимости метода предполагают, что f ′(x) и f ′′(x) сохраняют знак на промежутке [a;b].

Построение сходящейся последовательности производится по формуле

xk = xk−1 − f (xk−1 ) (C − xk−1 ) /( f (C) − f (xk−1 )), k =1,2,...,

(2.9)

где C – неподвижный конец промежутка.

Если f (a) f ′′(a) >0 , то за неподвижный конец принимается а, тогда x0 =b . В противном случае, неподвижен конец b, а в качестве нулевого

приближения выбирается а. На рис. 2.4 изображено поведение последовательных приближений в случаях:

	′′	б) f (a) <0 , f	′′
а) f (a) >0 , f			(a) <0
	(a) >0

Рис. 2.4 Процесс приближения продолжается до выполнения условия (2.5).

Порядок выполнения работы

1)Методом половинного деления (п.п. 1, 2) выбрать начальное приближение.

2)Выбрать подвижный конец промежутка и начальное приближение.

3)Вычислить приближенные значения корня по формуле (2.9) до выполнения условия (2.5).

Пример 2.3. Методом хорд найти значение корня уравнения 2 −lg x − x =0 с точностью ε =0,01.

Решение. 1) Для данного уравнения корень отделен и условие (2.3)

выполнено (см. пример 2.1).

lge

2) Найдем

f (a) = f (1) = 2 −lg1 −1 =1 >0 ,

′′

>0 .

f (a) = f

(1) =

Следовательно,

′′

f (a) f (a) >0 , откуда C=1, x0 = 2 .

3) Последовательно применяя формулу (2.9), получим

= x

−

f (x0 )(C − x0 )

= 2 −

f (2)(1 −2)

= 2 +

−0,301

=1,768 .

f (C) − f (x0 )

f (1) − f (2)

1 +0,301

= x

−

f (x1 )(C − x1 )

=1,768 −

f (1,768)(1 −1,768)

=1,756

, x

≈1,756 .

F(C) − f (x1 )

f (1) − f (1,768)

Корень уравнения принимаем равным 1,76, т.к. выполняется условие (2.5):

x3 − x2

1,756 −1,756

=0 <ε =0,01.

2.4 Метод Ньютона (метод касательных)

Сведения из теории

′

′′

Условия сходимости метода предполагают, что

f (x) и

f (x) сохраняют

знак на промежутке [a;b]. Уточнение значения корня производится путем построения сходящейся последовательности

xk = xk−1 −	f (xk−1 )	, k =1,2,3,...	(2.10)

	f ′(xk−1 )
За x0 принимается тот из концов промежутка [a;b], на котором
выполняется условие
f (x0 ) f ′′(x0 ) >0			(2.11)

Поведение последовательных приближений иллюстрируется на рис. 2.5.

а) f (a) <0 , f	′′	б) f (a) >0 , f	′′
а) f (a) <0 , f	(a) <0	б) f (a) >0 , f	(a) >0
		Рис. 2.5

Процесс приближения продолжается до выполнения условия (2.5).

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.12.2018215.55 Кб4ЛР№5.doc
#
19.08.2019484.86 Кб1марк в агро.doc
#
21.09.2019116.44 Кб2Маркетинг_МА-33.docx
#
20.09.2019426.5 Кб3маркировка!.doc
#
19.11.2019120.83 Кб4Масштаб.doc
#
01.03.2016575.29 Кб13матемVM_Санюкевич А.В._ч.1.pdf
#
01.03.2016721.03 Кб12матемVM_Санюкевич А.В._ч.2.pdf
#
01.03.2016510.45 Кб28Математическая статистика.pdf
#
19.07.2019283.14 Кб8материаловедение.doc
#
26.09.2019664.58 Кб72Мелиорация и водное хозяйство. Введение в специ...doc
#
25.04.2019113.71 Кб8Мелкие.docx