24. Приложение степенных рядов:приближённое вычисление значений функции, приближенное вычисление определенных интегралов, решение ду с помощью степенных рядов.

Ряд состоит из бесконечного числа членов => непосредственно по этой формуле использовать нельзя => ряд урезают => отбрасывают хвост и ограничиваются первыми n членами ряда.

||=||

Y=,с точностью

||=||<

Нужно взять столько членов ряда, чтобы погрешность была меньше .остаток ряда равен остаточному члену ряда. a<c<x

------------------------------------------------------------------------------

Если интеграл существуют, но его нельзя вычислить, пользуются разложением в степенной ряд. Степенной ряд можно почленно интегрировать сколько угодно разпо любому промежутку, лежащему в интервале сходимости. Если ряд удовлетворяет признаку Лейбница => погрешность по модулю меньше первого члена остатка.

Метод последовательного дифференцирования:

(с применением ряда Тейлора)

Y'’=f(x,y,y’) задача Коши

Из н у и

Из Y'’=f(x,y,y’) путём дифференцирования находим у'''.

Дальше дифференцируем по х, получаем разложение в ряд Тейлора.

Метод неопределенных коэффициентов:

Y’’+P(x)y’+q(x)y=r(x)

Y(0)=yo задача Коши

Y’(0)=y’o

P(x) и q(x) разложим в ряд по степеням х

Решение тоже будет в виде ряда с неизвестными пока коэффициентами.

Все разложения подставляем в данное ДУ.

Произведение рядов в левой части уравнения умножаются как многочлены. В результате получаем бесконечное разложение по степеням х. в последнем уравнении, содержащем бесконечноее число слогаемых, приравниваем коэффициенты при одинаковых степенях, в результате получаем бесконечную систему, решая её, находим коэффициенты .раскладываем у в ряд с этими коэффициентами.

23.Разложение и ряд Тейлора-Макларена элементарных функций

…+…

---------------------------------------------------------------

…+…

---------------------------------------------------------------

…+…

---------------------------------------------------------------

…+…

---------------------------------------------------------------

…+…

22.Разложение функций и степенной ряд. Ряд Тейлора.

Ряд Тейлора:

…

…+

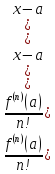
Если а=0, то ряд по степеням х расходится, а ряд Тейлора :

Теорема:

Для того, чтобы бесконечно дифференцируемая в точке а функция 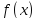, представляла сумму, составленного для неё ряда Тейлора необходимо и достаточно, чтобы(- остаточный член ряда)

- S(x)=-=0

Чтд

Следствие:

Пусть произведение любых n ограничены ||<k n(a-r; a+r) для

Тогда представляет сумму, составленную для него ряда Тейлора.

Если вимеет производные любых порядков, то:

1. Составим формально ряд Тейлора

…

2. Используя признаки Даламбера/Коши находим интервалы сходимости данного ряда (a-r; a+r)

3. Составим остаточный член ряда и находим то множествоХ при котором