8* Приложения тройного интеграла — объемы тел, масса тел, центр тяжести

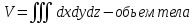
9* Криволинейный интеграл 1-го рода (КрИ-l): определение, свойства, вычисление, при­ложения

Рассмотрим в пространстве кривую АВ. Разобьем ее на точки. Найдем значение функции в каждой точке. Просуммируем. Рассмотрим предел. Если предел существует и конечный, то он называется КрИ1.

Теорема. Если функция непрерывна, а кривая гладкая или кусочногладкая, то для таких функций и кривых существует КрИ1.

1)КрИ1 не зависит от направления интегрирования.

2)Если для по прямой АВ

3)Постоянный множитель выносится за знак интеграла

4)Если АВ разбить точкой С на 2 части, то (АВ=АС+ВС)

1* Если кривая задана уравнениями

2* Если в полярной системе:

3*

10* Криволинейный интеграл 2-го рода (КрИ-ll): определение, свойства, вычисление, приложения

Рассмотрим в пространстве кривую АВ. Разобьем ее на точки. Найдем значение функции в каждой точке. Просуммируем. Рассмотрим предел. Если предел существует и конечный, то он называется КрИ2.

Теорема. Если функция непрерывна, а кривая гладкая или кусочногладкая, то для таких функций и кривых существует КрИ2.

1)Если поменять направление, то КрИ2 изменит знак.

2)Если для по прямой АВ

3)Постоянный множитель выносится за знак интеграла

4)Если АВ разбить точкой С на 2 части, то (АВ=АС+ВС)

1* Кривая задана уравнением y = f(x), x изменяется от до.

2* Кривая задана параметрически: x = x(t), y = y(t), t от до.

11* КрИ-ll по замкнутому контуру. Формула Грина. Независимость КрИ-ll от формы пути интегрирования

Движение точки по замкнутому контуру положительное, если при движении точки ограниченная область находится слева.

Теорема. Пусть плоская область D разбита на 2 области D₁ и D₂, причем L, L₁,L₂ – контуры, ограничивающие эти области.

Интеграл по контуру, ограничивающему область = сумме интегралов по контурам, ограничивающим составные части.

Теорема. Пусть P(x,y) и Q(x,y) непрерывны вместе со своими частными производными в односвязной области D, тогда:

Лемма. Для того, что бы КИ не зависел от формы пути интегрирования, НиД что бы КИ по любому замкнутому контуру (в области D) был равен нулю.

Теорема. Пусть P(x,y) и Q(x,y) непрерывны вместе со своими частными производными в односвязной области D. Тогда, для того что бы КИ не зависел от формы пути интегрирования НиД что бы во всех точках области выполнялось:

12* Общие понятия числового ряда. Геометрическая прогрессия и гармонический ряд

***Частичной суммой ряда называется сумма первых n членов: .

***Если , то ряд сходится и ему приписывают сумму S. Если этот или =, то ряд расходится

13* Основные свойства сходящихся рядов. Необходимый признак сходимости рядов

Š1* Если все члены сходящегося ряда с суммой S умножить на число k, то преобразованный ряд тоже будет сходиться, а его сумма kS

Š2* Даны 2 сходящихся ряда. Ряд полученный почленным сложением (вычитанием) тоже сходится

Š3* Если числовой ряд сходится, то сходится и ряд полученный из данного отбрасыванием или присоединением конечного числа членов

Š4* Если сходится ряд, то сходится и любой из его остатков, и наоборот

Š5* Если ряд сходится, то предел остатка =0

Необходимый признак сходимости ряда:

Если ряд сходится, то предел общего члена =0