29.Виды уравнений матем.Физики.Метод Фурье.Метод сеток.

Основные уравнения мат.физики:

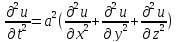
1.«волновое» уравнение;

Физ тело называется изотропным, если его тепловые свойства одинаковы во всех точках и по всем направлениям. В однородном изотропном теле процесс распределения тепла описывается

2.уравнением теплопроводности:

При установившемся тепловом состоянии, когда ,

уравнение теплопроводности переходит в

3. уравнение Пуассона:

Если нет тепла, уравнение теплопроводности переходит в

4.уравнение Лапласа:

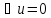
28. разложение в ряд Фурье периодических функций с общим периодом. разложение в ряд Фурье непериодических ф-ий.

Периодической функцией с периодом Т называется функция , если для неё выполняется равенство:

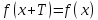
Пусть да на , с периодом 2

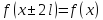
И удовлетворяет условиям Дерихле => может быть разложена в тригонометрический ряд, причём коэффициенты определяются по формулам:

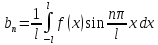
А)Для четных периодич.:

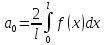
Б)Для нечетных периодич:

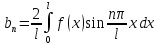
Непереодических :

1. Если разложена в триг. ряд с любым периодом, то в правой части период 2

Если непрерывна и задана на всей числовой оси => она не может быть разложена в ряд Ф.

2. Пусть функция задана на с Т=2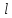, продолжим эту функцию на всю числ ось ; в состав новой входит первоначальная ф на, если удовл усл Дирихле => может быть разложена в ряд Ф

3. Пусть функция задана на продолжим произвольно на(разложим по чёт/нечёт) функция может быть продолжена набесчисл множеством способов и => можно получить бесчисл множ рядов, но все эти ряды на участкепредставляют

27.ряды Фурье для чёт/нечёт функций наз чёт, еслипри любом х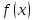наз нечёт, если

Свойства чёт и нечёт функций:

1. Произведение чёт на чёт или нечёт на нечёт функций есть функция чётная

2. Произведение чёт на нечёт есть функция нечётная

3. Если чётная =>

4. Если чётная =>

5. Если функция удовлетворяет условиям Дерике:

А)Для четных периодич.:

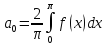
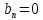
Б)Для нечетных периодич:

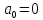
26. Сходимость ряда Фурье.Теорема Дирихле.

Условие Дирихле: функция на промежутке [a,b] удовлетворяет условию Дерике, если выполняются 2 условия:

1 на [a,b] или непрерывна, или имеет конечное число точек разрыва первого рода

2 на [a,b] кусочномонотонна

Достаточный признак разложимости функции в тригоном. ряд Фурье. Теорема Дирихле:

Пусть периодическая функция любом конечном промежутке удовлетворяет условию Дерике, тогда тригонометрический ряд, соответствующий этой функции

Сходится на всей числовой оси и имеет своей суммой , причём в точке разрыва функции, значение суммы ряда = среднему арифм. Значений функции слева и справа:

Точек разрыва конечное число=>их мало=>в основном сумма ряда совпадает с и только в точках разрыва получаются различия.

25. тригонометрический ряд Фурье. Коэффициенты Фурье.

[-]

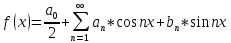
Геометрический ряд, коэфф которого определяются по формулам:

(коэффициенты Фурье (2))

наз тригонометрическим рядом Фурье