18.Электрические цепи с индуктивно связанными элементами (основные понятия, определения и характеристики).

Две катушки называются индуктивно связанными, если при изменении тока в одной из катушек приводит к наведению ЭДС в другой катушке (или к возникновению ЭДС катушки) такая ЭДС называется взаимной индукцией.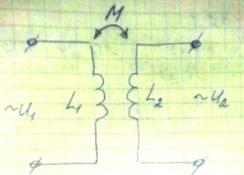

Ф₁₁ -> -e₁₁ = -L1 di₁/dt {ЭДС самоиндукции 1-ой катушки}

Ф₂₂ -> -e₂₂ = -L2 di₂/dt {ЭДС самоиндукции 2-ой катушки}

Ф₂₁- магнитный поток во 2-ой катушке, создающийся током в 1-ой катушке.

Ф₁₂- магнитный поток во 1-ой катушке, создающийся током в 2-ой катушке.

w₁-количество витков 1-ой катушки, w₂- количество витков 2-ой катушки.

ψ = |M₂₁ i₁| -потокосцепление во 2-ой катушке, создающийся током 1-ой.

ψ = |M₁₂ i₂| -потокосцепление в 1-ой катушке, создающийся током 2-ой.

M=M₂₁=M₁₂ – коэффициент взаимной индукции

e₂₁ =M₁₂ di₁/dt e₁₂=M₂₁ di₂/dt

e₁=e₁₁±e₁₂ - суммарная ЭДС в 1-ой катушке, состоящая из ЭДС самоиндукции ± ЭДС взаимоиндукции

e₂=e₂₁±e₂₂ - суммарная ЭДС во 2-ой катушке, \-\-\

+ согласно, - встречно

степень связи:

К₂₁= (-M di₁/dt)/(-L₁ di₁/dt)=M/L₁ - определяет, какая часть магнитного потока сцепляется с витками 2-ой катушки при прохождении тока в 1-ой;

K₁₂= (-M di₂/dt)/(-L₂ di₂/dt)=M/L₂

K=√K₁₂*K₂₁=M/(√L₁*L₂); 0<K<=1

М зависит от: взаимного расположения катушек, от количество витков в катушках, геометрического расположения, магнитной проницаемости среды

К зависит от: взаимного расположения катушек, намотки (плотность и количества витков катушки).

19.Способы определения взаимной индукции в электрических цепях с индуктивно связанными элементами.

Одноименные зажимы – зажимы, относительно которых направление тока будет одно и то же, при этом магнитные потоки самоиндукции и взаимоиндукции складываются.

Одноименные зажимы Ф₁₁↑↑Ф₂₂ e₁=e₁₁+e₁₂ e₂=e₂₁+e₂₂ - согласное соединение

Одноименные зажимы Ф₁₁↑↓Ф₂₂ e₁=e₁₁-e₁₂ e₂=e₂₁-e₂₂ - встречное соединение

При последовательном соединении:

u₁=i₁r₁-e₁ u₂=i₂r₂-e₂ u=u₁+u₂ =r₁i+L₁ di/dt ± Mdi/dt + r₂i+ L₂di/dt ±Mdi/dt

Z_экв=r_экв+jX_экв, r_экв=r₁+r₂

Xэкв=XL₁+XL₂±2X_M, X_L1=wL₁, X_L2=wL₂ X_M=wM, Lэкв=L₁+L₂±2M;

При параллельном соединении:

Z₁=r₁+jX_L1

Z₂=r₂+jX_L2

Z_M=jwM

I=I₁+I₂

U=I₁Z₁±I₂Z_M

U=I₂Z₂±I₁Z_M

При согласном включении: Zвх=(Z₁Z₂-Z²_M)/(Z₁+Z₂ - 2Z_M) -> I₁=U(Z₂ - Z_M)/(Z₁Z₂ - Z²_M)

При встречном включении: Zвх=(Z₁Z₂-Z²_M)/(Z₁+Z₂+2Z_M) -> I₂=U(Z₁ +Z_M)/(Z₁Z₂ - Z²_M)

20.Разветвленные электрические цепи с индуктивно связанными элементами (пример расчета и построение векторной диаграммы).

{воздушный трансформатор}

По 2-му закону Кирхгофа: I₁r₁+jX_L1I₁-jX_MI₂=U₁ , X_L=wL, X_M=wM

I₂r₂+jX_L2I₂-jX_MI₁+U₂=0

U₂=I₂(Z_H±X_M), K_T=w₂/w₁=E₁/E₂=I₂/I₁

21.Четырехполюсники (определения, классификация, системы уравнений, связь между коэффициентами)

Четырехполюсник – электрическая цепь, содержащая 4 зажима, из которых 2 входных и 2 выходных.

Четырехполюсник – это источник питания: 1)автономные(батарейка, аккумулятор); 2)неавтономные (усилитель резистора). Служит в качестве связного звена источника и приемника, обычно к зажимам 11’присоединяеться источника, а у 22’ – нагрузка.

Обычно задано 2-входных значения требуется определить 2-остальнхых значения(первичные параметры).

А-форма: U₁=A₁₁U₂+A₁₂I₂, I₁=A₂₁U₂+A₂₂I₂

B-форма: U₂=B₁₁U₁+B₁₂I₁, I₂=B₂₁U₁+B₂₂I₁

Z-форма: U₁=Z₁₁I₁+Z₂₁I₂, U₂=Z₂₁I₁+Z₂₂I₂

Y-форма: I₁=Y₁₁U₁+Y₁₂U₂, I₂=Y₂₁I₁+Y₂₂U₂

H-форма: U₁=H₁₁I₁+H₁₂U₂, I₂=H₂₁I₁+H₂₂U₂

G-форма: I₁=G₁₁U₁+G₁₂I₂, U₂=G₂₁U₁+G₂₂I₂

Определение А-параметров:

При холостом ходе (ХХ) относительно зажимов 22’(I₂=0)

А₁₁=U₁/U₂ {безразмерное}

A₂₁=I₁/U₂ {Сименсы}

При коротком замыкании (КЗ) относительно зажимов 22’ (U₂=0)

А₂₁=U₁/I₂ {Омы}

A₂₂=I₁/I₂ {безразмерное}

А₁₁А₂₂ - А₂₁А₁₂=1 – справедливо для всех пассивных четырехполюсников

Если А₁₁=А₂₂ - четырехполюсник симметричный

Y₁₂=Y₂₁- четырехполюсник взаимный

Четырехполюсник называется эквивалентный, если все входные в выходные величины равны.

Любой четырехполюсник можно представить в виде Г-образного, Т-образного и П-образного четырехполюсника.