9. Цепи синусоидального тока. Получение синусоидального эдс. Основные характеристики синусоидальных величин.

Переменный ток – электрический ток, изменяющийся с течением времени. Значение переменного тока, а также напряжение и ЭДС в любой момент времени t называется мгновенным значением. i=i(t), u=u(t), e=e(t)

Наибольшее из мгновенных значений периодически изменяющихся величин называется максимальными или амплитудными значениями и обозначаются U_m, I_m, E_m

Под переменным током обычно подразумевается синусоидальный ток – периодический электрический ток. Являющийся синусоидальной функцией времени. В электрических цепях синусоидальный ток создается под действием синусоидальной ЭДС. Генератор переменного тока состоит из электромагнита, между полюсами которого расположен якорь с обмоткой. При вращении якоря приводным двигателем с частотой α/t в витках возбуждается ЭДС.

Промежуток времени Т, в течение которого ЭДС (ток) совершает полное колебание и принимает прежнее по величине и знаку значение, называется периодом.

Число периодов в секунду – частота переменного тока. f=1/Т (Гц- герц)

Величина w- угловая частота = числу периодов за 2π секунд.

Действующее значение тока - это среднее квадратичное значение электрического тока за период, численно равное значению такого эквивалентного постоянного тока, при котором на сопротивлении выделяется такое же количество теплоты, как и при переменном. I=I_m/ √2

Если в начальный момент времени e(0)=E_m sin(0+α) – не равно нулю и будет определяться начальным углом α. Называемый фазовым углом или просто начальной фазой.

Получим e=E_msin(α)=E_msin(wt+α).

10. Способы представления синусоидальных величин (тригонометрическими функциями, графиками изменений во времени, вращающимися векторами, комплексными числами).

1)аналитическая (тригонометрическая) форма записи:

e=E_msin(ψ)=E_msin(wt+ ψe), i=I_msin(ψ)=E_msin(wt+ ψi), u=U_msin(ψ)=E_msin(wt+ ψu)

2)графическая

3)в виде радиус-вектора в декартовой системе координат

4)изображение синусоидальной величины на комплексной плоскости.

I_ma=I_mcosψ_i – активная составляющая, I_mp=I_msinψ_i – реактивная составляющая

ψ_i=arctg(I_mp/I_ma) I_m=√(I²_ma+I²_mp)

Im, Em, Um – комплексные амплитудные значения

I_m=(I_ma+jI_mp){алгебраическая}=I_m(cosψi+jsinψi){тригонометрическая}=I_me^jψi{показательная}

11. Неразветвленная цепь переменного тока с резистивным сопротивлением R, конденсатором емкостью С и катушкой индуктивностью L (сопротивления, проводимости, ток напряжение, мощность, векторная диаграмма )

12.Расчет и анализ сложной разветвленной электрической цепи переменного тока. Символический метод (последовательность, особенности и пример расчета).

Z₁=R₁–jX_L1= ; Z₂= j(X_L2– jX_C2)=; Z₃= j(X_L3– jX_C3)=; Z₄= R4= ; Z₅= R₅+j(X_L5 – X_C5)=; Z₆= R₆= ; Z₇= R7+j(X_L7 – X_C7)j=

Для мгновенных значений:

1 закон Кирхгофа: узел 1: i₁+i₂-i₅+j₁0,узел 2: i₆-i₂-i₁-i₇-j₁0,узел 3: i₇+i₅-i₄-j₄-i₃0

2 закон Кирхгофа: контур 030:

контур 0230:

контур 2132:

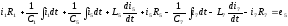
контур 212:

Для действующих значений:

1 закон Кирхгофа: узел 1: I₁+I₂-I₅+J₁=0, узел 2: I₆-I₂-I₁-I₇-J₁=0, узел 3: I₇+I₅-I₄-J₄-I₃=0,

2 закон Кирхгофа: контур 030: I₄*Z₄-I₃*Z₃0, контур 0230: I₆*Z₆+I₇*Z₇+I₄*Z₄0, контур 212: -I₂*Z₂+I₁*Z₁E₂, контур 2132: I₁*Z₁+I₅*Z₅-I₇*Z₇E₅