57 Сферическое движение тела

Сферическим движением(движением тела с одной закрепленной точкой) называется такое движение тела, при котором одна его точка О остается неподвижной во все время движения. Все остальные точки тела движутся при этом по траекториям, расположенным на поверхности сфер с центром в неподвижной точке О. Положение тела определяется углами Эйлера (рис. 1): углом прецессии φ, углом нутации θ и углом собственного вращения φ. Эти углы характеризуют положение координатного трехгранника осей Oξηζ, связанного с телом, по отношению к неподвижному трехграннику Oxyz. Линия ON пересечения координатных плоскостей Оху и Oξη называется линией узлов.

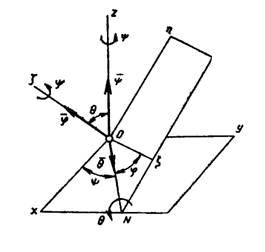
Рисунок 1.

Уравнения сферического движения:

РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ. Во всякий момент времени существует проходящая через неподвижную точку О прямая OΩ, скорости точек которой равны нулю. Это мгновенная ось вращения. Мгновенная угловая скорость  определяется соотношением

где  - векторы, численно равные производным углов Эйлера и направленные соответственно по осям z, ON и ζ. Мгновенная угловая скорость может менять свое положение в пространстве, описывая коническую поверхность, поэтому вектор углового ускорения

в общем случае не совпадает по направлению с  (рис. 2).

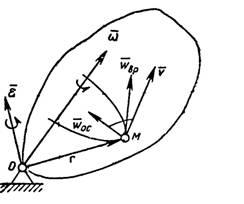
Рисунок 2.

Скорость точки при сферическом движении тела

или в аналитической форме (формулы Эйлера):

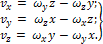
Ускорение точки складывается из осестремительной  и вращательной  составляющих (рис. 2):

58. Формулы Пуассона.

При рассмотрении вращательного движения тела вокруг неподвижной оси получена векторная формула Эйлера, по которой скорости точек тела полностью характеризуются общей для всех точек тела угловой скоростью вращения и расположением точек тела относительно оси вращения.

Cкоростьvкакой-либо точки М тела , по векторной формуле Эйлера:

υ= ω* r

Скорость какой-либо точки можно вычислить как первую производную по времени от радиуса-вектора г этой точки, проведенного из неподвижной точки. С другой стороны, скорость точки тела, вращающегося вокруг неподвижной точки, можно вычислить по векторной формуле Эйлера. Следовательно, производная по времени от радиуса-вектора любой точки твердого тела, вращающегося вокруг неподвижной точки, определится по формуле

dr/dt=ω*r

Длина радиуса-вектора г как расстояние между двумя точками твердого тела является постоянной величиной при движении этого тела. Следовательно, равенство dr/dt=ω*r можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого постоянен, и изменение этого вектора происходит только вследствие вращения его с угловой скоростью ш вместе с телом вокруг неподвижной точки.

Если взять подвижную систему координат Oxyz, скрепленную с телом, которое вращается вокруг неподвижной точки с угловой скоростью ω, то для единичных векторов i, j,kнаправленных по этим осям координат, как для векторов, модули которых постоянны имеем:

di//dt = ω*i ; dj/dt = ω *j; dk/dt = ω*k

Эти формулы называют формулами Пуассона.

59. Общий случай движения свободного твердого тела.

Любое движение свободного твердого тела

можно заменить совокупностью поступательных движений

вместе с какой-либо точкой тела и вращений вокруг этой

точки, совершаемых за то же время, что и истинное движение.

Поступательное движение вместе с точкой тела и подвижной системой координат является переносным движением, а движение тела относительно этой подвижной системы координат, являющееся в каждый момент времени вращением

вокруг своей мгновенной оси, проходящей через эту подвижную

точку тела, есть относительное движение.

Любое движение свободного твердого тела можно

составить из поступательного движения вместе с подвижной

системой координат и сферического движения относительно

этой системы координат. Для относительного сферического

движения можно ввести угловую скорость и угловое

ускорение, которое является первой производной по времени как в случае вращения тела вокруг неподвижной точки. Угловую скорость и угловое ускорение относительного вращательного движения вокруг какой-либо точки тела на-

называют в общем случае угловой скоростью и угловым ускорением свободного твердого тела. Эти величины не зависят от выбора точки тела. От выбора точки тела зависит только переносное поступательное движение тела.