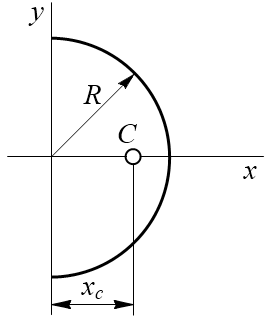
36. Центр тяжести дуги окружности, кругового сектора, полукруга.

Центр тяжести дуги окружности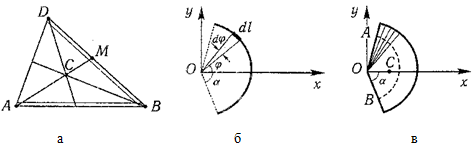

Дуга имеет ось симметрии. Центр тяжести лежит на этой оси, т.е.  y_C = 0.

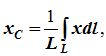
dl  – элемент дуги,  dl = Rdφ,  R – радиус окружности,  x = Rcosφ,  L = 2αR,

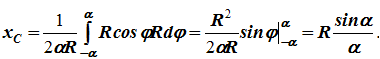
Следовательно:

 x_C = R(sinα/α).

Центр тяжести кругового сектора

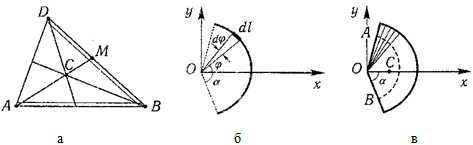
Сектор радиуса  R с центральным углом  2α имеет ось симметрии  Ox, на которой находится центр тяжести. 

Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса  (2/3)R. 

Центр тяжести сектора совпадает с центром тяжести дуги  AB:

Полукруг:

37. Кинематика. Кинематика точки. Способы задания движения точки.

Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил. Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный.

Кинема́тика точки  — раздел кинематики, изучающий математическое описание движения материпльных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t).

Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f₁(t), y=f₂(t), z=f₃(t).

Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде:f(x,y)=0 (для плоск-ти).

Векторный сп. положение точки определяется ее радиус-вектором , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора.

38.Связь между координатным и векторным, координатным и естественным способами задания движения точки.

СВЯЗЬ ВЕКТОРНОГО СПОСОБА С КООРДИНАТНЫМ И ЕСТЕСТВЕННЫМ выражается соотношениями:

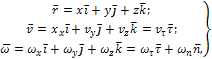
где  - орт касательной к траектории в данной точке, направленный в сторону отсчета расстояний, - орт нормали к траектории в данной точке, направленный в сторону центра кривизны (см. рис. 3).

СВЯЗЬ КООРДИНАТНОГО СПОСОБА С ЕСТЕСТВЕННЫМ. Уравнение траектории f(x, y)=z; f₁(x, z)=y получается из уравнений движения в координатной форме посредством исключения времени t. Дополнительным анализом значений, которые могут принимать координаты точки, определяется тот участок кривой 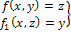, который является траекторией. Например, если движение точки задано уравнениями: x=sin t; y=sin²t=x², то траекторией точки является тот участок параболы у=х², для которого -1≤x≤+1, 0≤x≤1. Начало и направление отсчета расстояний выбираются произвольно, этим в дальнейшем определяется знак скорости и величина и знак начального расстояния s₀.

Закон движения определяется зависимостью:

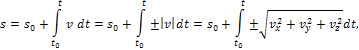
знак + или - определяется в зависимости от принятого направления отсчета расстояний.

39

Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения

Вектор скорости (v) — это расстояние, которое тело проходит в определенном направлении за единицу времени. Обратите внимание, что определение вектора скорости очень похоже на определение скорости, за исключением одного важного различия: скорость тела не указывает направление движения, а вектор скорости тела указывает и скорость, и направление движения. Следовательно, необходимы две переменные, которые описывают вектор скорости тела: скорость и направление. Физические величины, у которых есть значение и направление, называют векторными величинами.

Вектор скорости тела может время от времени изменяться. Если или его скорость, или направление изменяются, скорость тела также меняется. Постоянный вектор скорости подразумевает неизменную скорость и неизменное направление, тогда как термин «постоянная скорость» подразумевает только неизменное значение, не принимая во внимание направление. Термин «вектор скорости» часто используется попеременно с термином «скорость». Они оба выражают расстояние, которое тело проходит в единицу времени

40

Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.

Вектор ускорения

это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

где  – вектор ускорения.

Направление вектора ускорения совпадает с направлением изменения скорости Δ =  - ₀ (здесь ₀ – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t1 (см. рис 1.8) тело имеет скорость ₀. В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ =  - ₀. Тогда определить ускорение можно так:

41