Плотность вероятности.

Вероятность встретить частицу в некоторой малой области пространства пропорциональна не только квадрату амплитуды волновой функции, но и величине объема dV этой области, т.е.

.

С другой стороны, квадрат амплитуды волновой функции (2.7) можно найти, умножив комплексно сопряженную функцию Ψ* на Ψ

Таким образом,

и, следовательно, квадрат модуля волновой функции

представляет собой плотность вероятности найти частицу в данной точке пространства, т.е. вероятность, отнесенную к единице объема. Этот смысл выражение (2.9) сохраняет и в том случае, когда частица не является свободной, и ее волновая функция уже не определя­ется формулой (2.7).

Квадрат амплитуды волновой функции (2.7) для свободной час­тицы – постоянная величина (не зависит от координат частицы). Это значит, что плотность вероятности найти частицу во всех точках пространства одна и та же. С одной стороны, это можно объяснить тем, что плоская монохроматическая волна заполняет все пространство не имея ни начала, ни конца. С другой стороны, плоская монохроматичес­кая волна имеет вполне определенные длину волны λ и направление распространения. Следовательно, величина импульса и его направление также строго определены (известны все три проекции импульса). Если же какая-либо из проекций импульса, на­пример р_х известна точно, то неопределенность Δр_х = 0. Но в этом случае, согласно соотношению неопределенностей () долж­на быть бесконечно большой неопределенность Δх соответствующей координаты, т.е. частица с одинаковой вероятностью может казаться в любой точке пространства.

Операторы.

Нам нужно получить дифференциальное уравнение для волновой функции. Поэтому посмотрим, что получается при дифферен­цировании волновой функции (2.7) по времени и координатам. Продифференцируем сначала выражение (2.7) во времени:

Умножив обе части этого равенства на iћ, получим

Математический символ, указывающий, какие действия (операции) нужно совершить над стоящей справа от него функцией, называется оператором. В данном случае оператором является постоянный множи­тель iћ и знак производной по времени , т.е. символ . Этот оператор действует на функцию . В результате действия оператора получается та же функция, умноженная на величину энергии E.

Бели в результате действия оператора на функцию получается та же функция, умноженная на постоянный коэффициент, имеющий смысл не­которой физической величины, то

1. оператору приписывается название этой физической величины; обычно он обозначается той же буквой, что и эта физическая величина, с ломаной линией ("крышечкой") наверху;

2. функция называется собственной функцией этого оператору;

3. коэффициент, на который умножается функция, называется собственным значением оператора.

Таким образом, символ

является оператором полной энергии частицы, волновая функция сво­бодной частицы (2.7) - собственной функцией оператора полной энергии, а величина энергии E - собственным значением этого опе­ратора.

Так как в результате дифференцирования волновой функции (2.7) по координатам и умножения полученных выражений на – iћ получается

то символы

называются операторами проекций импульса.

Функция (2.7) является одновременно собственной функцией операторов всех проекций импульса, в величины проекций – собственными значениями этих операторов.

За оператор координаты принимают саму координату, т.е. . Действие оператора координаты на функцию сво­дится к умножению этой функции на координату.

С операторами согласно определенным правилам можно произво­дить действия: сложение и умножение. Результатом действия суммы операторов на некоторую функцию является сумма результатов действий на эту функцию каждого оператора по отдельности. Произведением же операторов называется последовательное действие на функцию двух операторов: сначала на функцию действует один оператор (стоящий ближе к ней второй сомножитель), затем результат этого действия подвергается действию второго оператора (первого сомножителя).

В частности, квадрат оператора проекции импульса на ось Оx действует на функцию Ψ следующим образом:

Действие квадратов других проекций импульса аналогично. Следовательно,

В квантовой механике при помощи сложения и умножения из опера­торов составляют новые операторы, которые носят название физических величин, по аналогии с которыми они составлены. Например, частица массы m с импульсом p имеет скорость . Так как квад­рат импульса частицы , то кинетическая энергия этой частицы

Если в этом выражении квадраты проекций импульса, заменить соответствующими операторами (2.14), то получится оператор кинети­ческой энергии

Здесь – дифференциальный оператор, который в математике носит название оператора Лапласа.

При двукратном дифференцировании волновой функции свободной частицы (2.7) по какой-либо координате функция умножается на и на квадрат соответствующей проекции импульса. Поэтому, действуя оператором на волновую функцию (2.7), найдем

т.е. в этом случае получается та же функция, умноженная на величину кинетической энергии.

Уравнение Шредингера.

Чтобы иметь представление о свойствах дифференциального уравнения, которому должна удовлетворять волновая функция частицы, рассмотрим волновое уравнение (2.1) для напряжен­ности электрического поля. Продифференцировав (2.5) дважды по x и по t, найдем

Подставив эти выражения для производных в уравнение (2.1) и сократив на общие множители, получим после извлечения квадратного корня из обеих частей равенства

т.е. подстановка волновой функции в волновое уравнение в случае плоской монохроматической электромагнитной (световой) волны приводит к соотношению между энергией и импульсом для светового кванта.

Будем считать, что в случае свободной частицы, волновая функ­ция которой (2.7) также соответствует плоской монохроматической волне, волновое уравнение должно удовлетворять этому же условию, т.е. после подстановки в него волновой функции должно получиться соотношение между энергией и импульсом частицы. Свободная частица имеет только кинетическую энергию. Поэтому ее полная энергия связана с импульсом p, согласно формуле (2.15), соотношением

Дифференцирование волновой функции мы можем заменить действием на нее операторов. В частности, мы нашли, что волновая функция свобод­ ной частицы (2.7) умножается в результате действия на нее опера­тора полной энергии (2.11) на величину E энергии частицы, а в результате действия оператора кинетической энергии (2.16) на ве­личину . Поэтому, если мы напишем уравнение для волновой функции частицы (2.7) в виде

то после действия операторов получится

и после сокращения на Ψ будет выполнено соотношение (2.18).

Если в уравнение (2.19) подставить выражения для операторов, мы придем к дифференциальному уравнению для волновой функции свобод­ной частицы, удовлетворяющему сформулированному выше условию:

Само по себе это уравнение не дает ничего нового, так как его ре­шением являются волновые функции вида (2.7) для свободной час­тицы, которые были использованы для составления уравнения. Кроме того, практически всегда приходится иметь дело не со свободными частицами, а с частицами, взаимодействующими друг с другом или подвергающимися воздействию какого-либо поля. Таким образом, урав­нение (2.20) следует видоизменить, чтобы в нем учитывались воздей­ствия, которым подвергается частица.

Полная энергия частицы, подвергающейся какому-либо воздействию, складывается из кинетической энергии T и потенциальной энергии U. Поэтому можно предположить, что уравнение (2.19) в случае частицы, подвергающейся воздействию, должно быть заменено уравнением

где – оператор потенциальной энергии. Примем в качестве гипо­тезы, что оператор потенциальной энергии совпадает с самой потенциальной энергией U.

Тогда, заменив в уравнении (2.21) операторы их выражениями, нридем к уравнению

Это уравнение называется уравнением Шредингера и является основным уравнением квантовой механики. Поскольку мы пришли к этому уравнению после целого ряда предположений (комплексная вол­новая функция, соответствие между операторами и физическими вели­чинами, вид оператора потенциальной энергии), то следствия, выте­кающие из этого уравнения, должны быть проверены на опыте. Как уже говорилось выше, эти следствия очень хорошо подтверждаются опытны­ми фактами. Следует только отметить, что уравнение (2.22) верно лишь при описании движения частиц, скорость которых значительно меньше скорости света, так как соотношение (2.15) между кинетичес­кой энергией и импульсом справедливо лишь при этом условии. В ре­лятивистском же случае для описания волновых свойств частицы сле­дует пользоваться другими уравнениями (Дирака, Клейна-Гордона).

Уравнение Шредингера в стационарном случае. Вообще говоря, потенциальная энергия U зависит от координат частицы и времени и времени t. Если же U от времени не зависит (стационарное движение) и, следовательно, полная энергия E также не меняется с течением времени, то волновую функцию можно представить в виде двух сомножителей:

Первый сомножитель зависит только от времени, а второй - толь­ко от координат. Подставив волновую функцию (2.23) в уравнение (2.22), получим, учитывая, что в левой части уравнения нужно диф­ференцировать только первый множитель, а в правой - только второй:

Сократив на , найдем уравнение для функции (так называемое стационарное уравнение Шредингера)

Здесь E – величина полной энергии – постоянное число.

Плотность вероятности в стационарном случае равна квадрату модуля функции , так как

Таким образом, чтобы найти плотность вероятности в стационар­ном случае, нужно решить уравнение (2.24) при заданной зависимос­ти потенциальной энергии частицы от ее координат. Всякое дифферен­циальное уравнение имеет единственное решение лишь при определен­ных условиях, накладываемых на функцию. Эти условия обычно опреде­ляются физическим смыслом функции и ее значениями на границах области. Естественно считать, что плотность вероятности есть непре­рывная функция координат, везде конечная и однозначная. Очевидно, эти же условия должны выполняться и для функции . Кроме того, чтобы можно было пользоваться уравнением, в которое входят вторые производные функции по координатам, необходимо, чтобы эти вторые производные существовали, а для этого нужно, что­бы первые производные были также непрерывными и конечными.

Разделим возможные случаи движения на два вида:

1. Потенциальная энергия такова, что при заданной полной энергии частица находится в ограниченной области пространства. Тогда вероятность того, что частица находится внутри этой области, представляет собой вероятность достоверного события. Принято считать, что вероятность достоверного события равна единице. Разобьем эту область на элементарные объемы dV. Вероятность найти частицу в каждом таком объеме, согласно формулам (2.8) и (2.25), . Вероятность же W того, что частица находится внутри области в любом из этих объемов, равна сумме вероятностей dW (согласно формуле о сложении вероятностей). В данном слу­чае суммирование сводится к интегрированию по объему V всей области и, следовательно,

Это условие называется условием нормировки, а функции, удовлет­воряющие ему - нормированными функциями. Если функция Ψ не нор­мирована, то ее можно нормировать, умножив на постоянный множитель. Область, в которой находится частицн, может занимать и все простран­ство. Однако при этом нужно потребовать, чтобы функция Ψ убывала с расстоянием r от начала координат быстрτе чем 1/r, иначе интеграл (2.26) обращается в бесконечность.

2. Частица может уйти в бесконечность, как, например, в случае свободного движения, когда решением уравнения (2.22) является плос­кая волна (или сумма плоских волн), и плотность вероятности не уменьшается с увеличением расстояния от начала координат. В таких случаях условие нормировки оказывается более сложным. Им, однако, практически пользуются редко, так как в большинстве случаев доста­точно знать отношение плотностей вероятности в различных областях пространства.

Частица в потенциальной яме.

В качестве примера рассмотрим решение уравнения Шредингера (2.24) для частицы, находящейся в потенциальной яме с бесконечно высокими стенками и движущейся вдоль координатной оси Оx (одномерное движение). График потенциальной энергии U(x) для этого случая приведен на рис. 2.2.

Рис. 2.2

Потенциальная энергия равна нулю при (область I) и бесконечно велика при и (области 2 и 3). Возрастание потенциальной энергии скачком от нуля до бесконечности соответствует тому, что при приближении частицы, находя­щейся внутри ямы (в области I) к стен­кам (точкам и ) возникают бесконечно большие силы, препятствующие движению частицы. Рассматриваемый здесь случай весьма идеализирован, однако на нем хорошо видны особенности решения задач квантовой ме­ханики в случае движения частицы в ограниченной области.

При одномерном движении вдоль оси Оx волновая функция зависит лишь от одной переменной x, ее производные и равны нулю, и уравнение (2.24) в области 1 (U = 0) принимает вид

или

Здесь E > 0, поскольку потенциальная энергия U = 0, а полная энергия больше потенциальной.

Чтобы решить уравнение (2.27), нам нужно найти такую функцию Ψ(x), вторая производная которой по x пропорциональна самой функции, взятой с обратным знаком. Как известно, такой функцией в самом общем случае является

где C, β, α – неизвестные постоянные, которые следует определить при помощи дополнительных условий, накладываемых на волновую функ­цию.

Чтобы найти постоянные α и β, рассмотрим значения, которые функция Ψ(x) принимает на границах области 1, т.е. при x = 0 и при x = l. В области 2 и 3 частица проникнуть не может, поэтому внутри них волновая функция тождественно равна нулю. Так как волно­вая функция должна быть непрерывной, то функция (2.28) при x = 0 и при x = l также должна обращаться в нуль. Следовательно, откуда и . Условие выполняется теперь при , где n – целое число, т.е. необ­ходимо, чтобы

Таким образом, мы имеем целый набор волновых функций вида

удовлетворяющих условиям на границах области и соответствующих различным значениям n.

Величину коэффициента С можно найти при помощи условия норми­ровки. В одномерном случае представляет собой вероятность найти частицу в интервале dx. Так как частица не может выйти из области l, то вероятность найти ее внутри этой области (вероятность достоверного события)

Вычислим величину интеграла

Сделав замену переменной

и учитывая известную формулу

получим после ряда преобразований

Согласно условию нормировки (2.31), .

Следовательно, , и волновая функция

Чтобы окончательно убедиться в справедливости полученного решения, представим волновую функцию (2.32) в исходное уравнение (2.27):

После сокращения общих множителей получим

т.е. уравнение (2,27) удовлетворяется не при любых значениях энергии частицы, а лишь при некоторых значениях, зависящих от целого числа n:

Итак, для описания движения частицы в потенциальной яме с бесконечными стенками мы получили набор волновых функций (2.32) и ряд соответствующих этим функциям отдельных "дозволенных" значений (2.33) энергии частицы – так называемый дискретный энергетический спектр. Значения энергии и волновые функции опреде­ляют состояние, в котором находится частица, и зависят от кванто­вого числа n. Это число может принимать целые положительные зна­чения, начиная с единицы (n = 1, 2, 3,…).

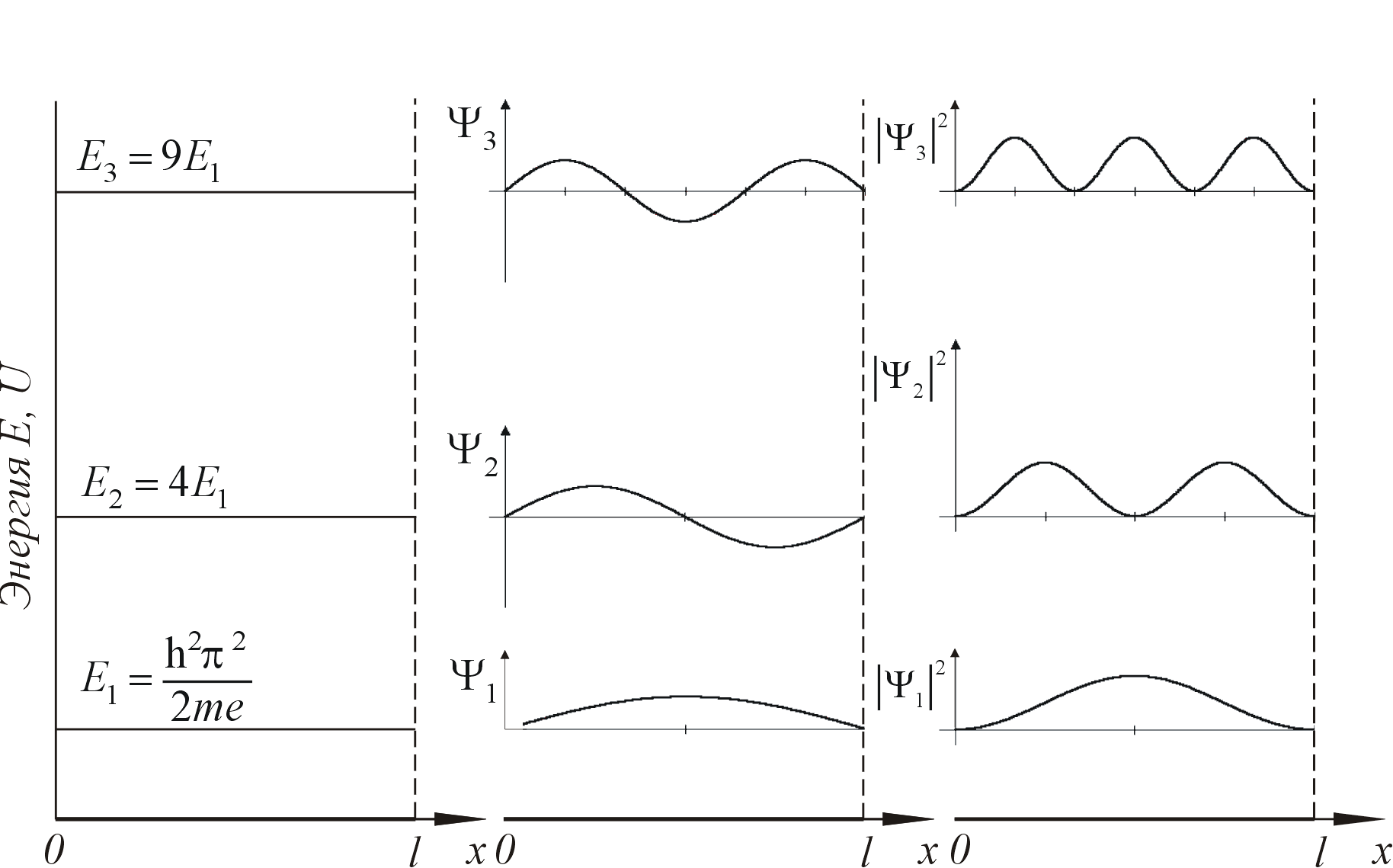
а) б) в)

Рис. 2.3

На рисунке 2.3 изображены:

1. три первых значения полной энергии частицы, нанесенных на график потенциальной энергии. Эти значения энергии на графике изображаются прямыми горизонтальными линиями, так как полная энергия не зависит от положения частицы, и называются поэтому уровнями энергии;

2. волновые функции, со­ответствующие этим значениям энергии;

3. зависимость плотности вероятности |Ψ(x)|² для этих трех случаев от координаты частицы x.

Заметим, что в классическом случае, в отличие от квантового, когда движение частицы описывается законами Ньютона, плотность ве­роятности нахождения частицы одинакова в любом месте потенциальной ямы с горизонтальным дном. В самом деле, в этом случае кинетическая энергия постоянна. Следовательно, постоянна и скорость частицы. Поэтому в одинаковых интервалах dx частица находится одинаковые промежутки времени.

Что же касается квантования энергии, т.е. существования отдельных строго определенных значений энергии, то вообще это характерная особенность квантового движения частицы не только в данном случае, но и всегда, когда движение частицы происхо­дит в ограниченной области.

Прохождение частиц через потенциальный барьер (туннельный эффект).

В классическом случае наглядной моделью прохождения частицы через потенциальный барьер может служить перекатывание шарика (без трения) через горку, лежащую на его пути. Потенциальная энергия шарика в поле силы тяжести про­порциональна высоте точек горки, в которых находится ша­рик. Поэтому график потенциальной энергии шарика (рис. 2.4) также имеет вид горки (отсюда и название "потенциальный барьер").

По мере вкатывания шарика на горку возрастает его потенци­альная энергия и убывает кинетическая, в то время как полная энергия шарика Е, согласно закону сохранения энергии, оста­ется постоянной (на графике она изображается прямой горизонталь­ной линией - уровнем энергии). Если полная энергия шарика меньше максимальной потенциальной энергии барьера , то шарик вкатится на горку лишь до точки с координатой потенциальная энергия в которой равна полной энергии, а затем скатится обрат­но. Если же полная энергия шарика больше максимальной потенциаль­ной энергии, то шарик перекатится через горку. Поскольку мы здесь при описании движения шарика пользовались только законом сохра­нения энергии, то эти рассуждения будут верны и для описания движения частицы в случае потенциальной энергии любого происхождения, лишь бы график ее имел вид барьера.

С точки зрения квантовой механики, когда существенны волновые свойства, прохождение частиц через потенциальный барьер больше похож на прохождение света через слой вещества, на грани­цах которого меняется показатель преломления. В самом деле, при прохождении частицы через потенциальный барьер в области барьера меняется кинетическая энергия частицы. Следовательно, меняется ее импульс и связанные с импульсом длина волны и скорость частицы, совершенно аналогично тому, что при прохождении света через гра­ницу, разделяющую среды с различными показателями преломления, меняется длина волны и скорость распространения света.

Как известно, при падении света на границу, разделяющую среды с различными показателями преломления, световая волна частич­но проходит через эту границу (преломляется), частично же отража­ется и идет в обратном направлении. Для частиц в случае прохожде­ния потенциального барьера мы вправе также ожидать наличие прохо­дящей и отраженной волн. Поскольку волны, связанные с частицами, определяют вероятность поведения частиц, то можно сказать, что для частицы, падающей на потенциальный барьер, существует вероят­ность как пройти через этот барьер, так и отразиться от него об­ратно. Иначе говоря, если на барьер падает пучок частиц одинаковой энергии, то некоторые частицы из этого пучка проходят через барьер, другие же от него отражаются.

Рис. 2.4 Рис. 2.5

Вероятность прохождения (коэффициент проницаемости барьера, или его прозрачность) можно определить как отношение числа частиц, прошедших барьер в течение некоторого времени, к числу частиц, падающих на барьер за это же время.

Мы рассмотрим прохождение частиц через потенциальный барьер простейшей прямоугольной формы в одномерном случае, т.е. будем считать, что потенциальная энергия U(x) частицы, движущейся вдоль оси Ох (рис. 2.5), равна нулю при x < 0 (область I), постоянна и равна по величине U₀ при (область 2) и снова равна нулю при (область 3). Учитывая, что при одно­мерном движении вдоль оси Оx производные волновой функции и равны нулю, напишем для каждой из трех областей стационарное уравнение Шредингера (2.24) в виде:

где для краткости введены обозначения

(2.35,б)

Решениями этих уравнений в самом общем виде являются функции

(2.36,б)

(2.36,в)

где – коэффициенты, значения которых нужно определить при помощи дополнительных условий, накладываемых на волновую функцию.

Функции представляют собой, по сути дела, волновые функции свободной частицы. В самом деле, согласно (2.15) квадрат импульса p² частицы связан с ее кинетической энергией T соотно­шением . Но T = E в областях I и 3 и T = E – U₀ в облас­ти 2. Поэтому

и

где p₁ – импульс частицы в областях I и 3 и p₂ – импульс части­цы в области 2 (при E > U₀). Чтобы получить полную волновую функ­цию, нужно согласно (2.23), умножить Ψ(x) на . В частности, в области I полная волновая функция будет иметь вид

В этом выражении первый член представляет собой волну вида (2.22), распространяющуюся слева направо (в положительном направ­лении оси Оx), а второй член, в котором импульс имеет противопо­ложный знак по сравнению с импульсом в первом члене - волну, рас­пространяющуюся справа налево. Волна, распространяющаяся слева на­право, соответствует частицам, движущимся в сторону барьера. Вол­на, распространяющаяся в противоположную сторону, представляет собой отраженную от барьера волну и соответствует частицам, движущимся от барьера налево.

Решение (2.36,в) в области 3 также содержит волны, распространяю­щиеся в обе стороны. Однако если мы примем, что на барьер падают частицы, движущиеся в положительном направлении оси Ох, то справа от барьера могут оказаться лишь частицы, прошедшие через барьер и движущиеся в том же направлении. Чтобы учесть это обстоятельство, мы исключим в области 3 волну, распространяющуюся в сторону барье­ра, положив равным нулю коэффициент b₃.

В области 2 вид решения зависит от того, что больше - потен­циальная энергия U₀ или полная энергия E. Если E > U₀, то правая часть в формуле (2.35,б) положительна, q – действительное число и решение (2.36,б) также содержит две волны: волну, прошедшую через левую границу (х = 0) барьера, и волну, отразившуюся от его правой границы (x = l).

Коэффициент a₁ в выражении (2.36,a) связан с интенсивностью пучка частиц, падающего на барьер, и поэтому может быть задан про­извольно. Оставшиеся четыре коэффициента , как мы увидим в дальнейшем, при любой энергии E частицы однозначно определяются при помощи дополнительных условий, накладываемых на волновую функцию. Таким образом, в областях I и 2, согласно квантовой механике, должны существовать волны, отраженные от левой и правой границ барьера. Это значит, что если даже энергия частицы больше максимальной энергии барьера, некоторая доля частиц от барь­ера отражается обратно. В классической механике, как уже упомина­лось, такой эффект невозможен. В то же время наличие волны, прошед­шей через барьер (коэффициент a₃ не равен нулю), не противоречит в этом случае выводам классической механики.

Рассмотрим подробнее более интересный случай, когда полная энергия E частицы меньше высоты барьера U₀, и законы класси­ческой механики вовсе не разрешают частице пройти через этот барь­ер. В этом случае, согласно формуле (2.35,б), – мнимое чис­ло, причем

Учитывая значение q, а также то, что b₃ = 0, перепишем функции, представляющие решение уравнений (2.34), в виде:

(2.38,б)

(2.38,в)

Здесь для удобства дальнейших выкладок функцию Ψ₃ мы умножили на постоянный множитель .

Заметим еще, что в области 2 функция (2.38,б) уже не соответ­ствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент в этом случае не мнимые, а действитель­ные.

Чтобы найти коэффициенты при произвольном коэффициенте а₁, воспользуемся дополнительными условиями, накла­дываемыми на волновую функцию. Так как наша волновая функция представлена в областях 1,2 и 3 тремя различными формулами (2.38,а, б, в), то мы должны потребовать, чтобы в точках, лежащих на границах областей, т.е. при х = 0 и x = l, волновая функция и ее производная по х были бы непрерывными. Найдем производные функций (2.38,а, б, в):

(2.39,б)

(2.39,в)

Приравнивая при х = 0, при x = l, получим систему четырех уравнений для определения четырех коэффициентов :¹

(2.40,б)

(2.40,в)

(2.40,г)

Коэффициентом проницаемости D потенциального барьера мы назвали отношение числа прошедших через барьер частиц к числу час­тиц, падающих на него за то же время. Эта величина равна отноше­нию вероятности встретить частицу после прохождения барьера по его правую сторону к вероятности встретить частицу в падающем на барь­ер .пучке частиц. Так как вероятности пропорциональны квадратам модулей амплитуд соответствующих волн, то

Таким образом, чтобы найти коэффициент проницаемости, нам достаточно из уравнений (2.40,а, б, в, г) найти отношение . Для этого выразим из уравнений (2.40,в, г) коэффициенты через коэффициент :

(2.42,б)

Чтобы упростить вычисления, будем считать, что , как это часто бывает в практически важных случаях. Тогда в уравнениях (2.40,а, б) можно пренебречь коэффициентом а₂ по сравнению с b₂, а затем исключить из этих уравнений коэффициент b₁. В результате, учитывая (2.42,а), получим

Отсюда

и, следовательно, согласно (2.41), коэффициент проницаемости барьера

Подставив сюда значения , определяемые формулами (2.35,а) и (2.37), найдем

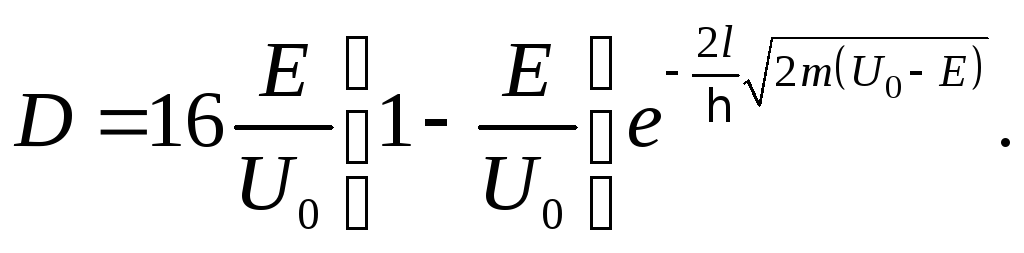
При E < U₀, когда , величина 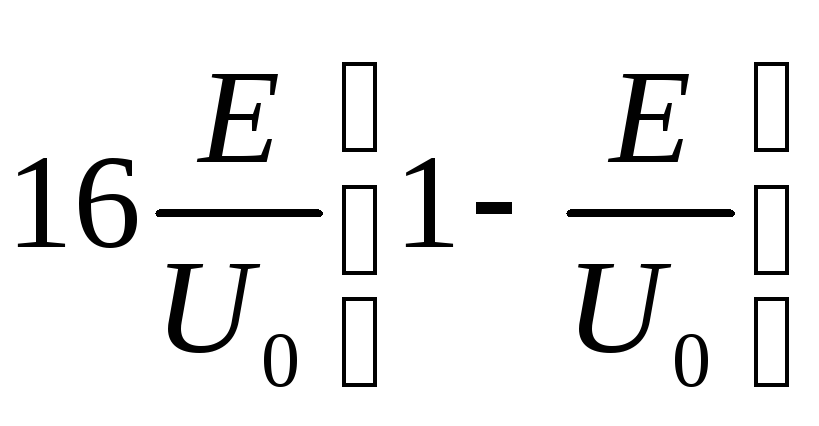лежит в пределах от нуля до четырех. При грубых расчетах ее обычно полагают равной единице. Поэтому окончательно коэффициент прони­цаемости потенциального барьера прямоугольной формы приближенно можно вычислить по формуле

Таким образом, хотя по законам классической механики при E < U₀ частица не в состоянии преодолеть потенциальный барьер, в квантовой механике коэффициент проницаемости барьера отличен от нуля и может достигать заметной величины, если малы разность (U₀ – E) и ширина барьера l. Например, для электронов при (U₀ – E) = 1 эВ и l = 5·10^–8 см, D ≈ e^–5,1 ≈ 0,006, т.е. через барьер проходит шесть электронов из каждой тысячи.

С классической течки зрения прохождение частицы через барьер при E < U противоречит закону сохранения энергии. С квантовой точки зрения такого противоречия нет. Чтобы убедиться в этом, обратимся к соотношению неопределенностей. Если мы хотим определить, прошла частица через барьер или нет, мы должны изме­рить ее координату x с ошибкой Δx, не превышающей ширину барьера l. Следовательно, ошибка в импульсе p_x частицы должна быть

С другой стороны, чтобы коэффициент проницаемости D не был слишком мал, необходимо, чтобы показатель степени в формуле не был слишком велик. Например, если , то (напомним, что ).

Поэтому будем считать, что .

Тогда

Заметим теперь, что если частице добавить кинетическую энер­гию и, следовательно, согласно (2.15), сообщить им­пульс , то она сможет пройти через барьер без нарушения закона сохранения энергии. Из неравенства (2.44) следует, что сообщенный частице импульс должен быть меньше неопре­деленности в импульсе. Иначе говоря, при прохождении частицы через потенциальный барьер в квантовой механике энергия сохраняется с точностью, которая вообще допустима при одновременном измерении координат и импульса частицы.

При помощи формулы (2.43) можно найти коэффициент проницае­мости D и в случае барьера произвольной формы. Для этого пред­ставим такой барьер в виде суммы элементарных прямоугольных барьеров равной ширины Δx (рис. 2.6). Высота элементарного барьера равна значению потенциальной энергии U(x) в середине промежутка Δx. Коэффициенты проницаемости каждого из них по отдельности будут

Здесь учтены лишь те из элементарных барьеров, для которых E < U(x), так как при E > U(x) коэффициент проницаемости очень близок к единице.

Рис. 2.6

Вероятность прохождения частицы через весь барьер представляет собой вероятность сложного собы­тия, состоящего из прохождения частицы через все элементарные барьеры, и равна произведению вероятностей прохождения через каждый элементарный барьер по отдельности (согласно теореме об умножении вероятностей). Следовательно, коэффициент проницаемости всего барьера

При стремлении Δx к нулю сумма в показателе степени переходит в интеграл, пределами которого являются координаты точек x₁ входа частицы в барьер и x₂ выхода ее из барьера.

Таким образом, коэффициент проницаемости в случае барьера произвольной формы

.

Прохождением частиц через потенциальный барьер объясняется целый ряд явлений: внешняя контактная разность потенциалов при соприкосновении разнородных проводников, холодная эмиссия электронов (испускание электронов с поверхности проводника при напряженности электрического поля вблизи этой поверхности свыше 100 кэВ/см), некоторые особенности ядерных реакций, α-распад ядер и т.д.

1 Из системы уравнений (2.40) можно найти коэффициенты также и в том случае, если E > U₀. для этого достаточно заменить в ней на .

24