32

серийный (выбирается не объект, а серия и подвергается сплошному обследованию (дневная продукция цеха) – один раз в некоторый промежуток времени);

комбинированый (смешивают в разумных рамках приведенное выше).

21.2. Обработка статистических данных

Пусть из генеральной извлечена выборка некоторого объема. Значения xi исследуемого признака Х называют вариантами.

Комментарий. Термин варианта – женского рода.

Расположим варианты в порядке возрастания их значений и получим дискретный вариационный ряд. Если выборка имеет большой объем (более 30 вариант) и/или исследуемый признак непрерывен, то строят интервальный вариационный ряд. О построении интервального вариационного ряда будет сказано ниже. Как всякий перечень значений признака Х вариационный ряд дает некоторое представление о генеральной.

Может оказаться, что некоторые или многие варианты повторяются. Тогда их группируют. Если несколько вариант равны значению xi , то говорят, что варианта имеет частоту ni . Естественно, что ∑ ni = n – объему выборки.

Если частоту ni разделим на объем выборки n, то получим

частотами . Числа Nni называют относительными накопленными частотами.

Пусть выборка имеет большой объем и/или исследуемый признак Х (генеральная) непрерывен. Тогда статистику (экспериментальные данные, выборку) следует обработать в таком порядке:

найти минимальную хmin и максимальную xmax варианты выборки; найти размах вариаций R= xmax - хmin;

R

найти шаг h интервального вариационного ряда h=1+3,2ln n ; чаще

просто разбивают интервал [хmin; xmax] на 5 – 15 интервалов (частей); меньше не берут, чтобы не потерять характер изменения Х; а больше не берут, чтобы ряд был обозримым;

договариваются об отнесении граничных точек интервалов; дело в том, что некоторые варианты могут совпадать с границами интервалов; чтобы пользователю было известно все о данной статистике, его нужно обо всем предупредить;

подсчитывают частоты ni – количество вариант, попадающих в выбранный интервал.

После этого приступают к формированию статистических распределений выборки.

21.3. Статистические распределения

32

33

Таблица, первую строку(столбец) которой занимает вариационный ряд (дискретный или интервальный), а вторую строку(столбец) занимают частоты,

называется статистическим распределением выборки по частотам.

Такая же таблица, где вторую строку(столбец) занимают относительные частоты, называется статистическим распределением выборки по относительным частотам .

Такая же таблица, где вторую строку(столбец) занимают накопленные частоты, называется статистическим распределением выборки по накопленным частотам .

Такая же таблица, где вторую строку(столбец) занимают относительные накопленные частоты, называется статистическим распределением выборки по относительным накопленным частотам .

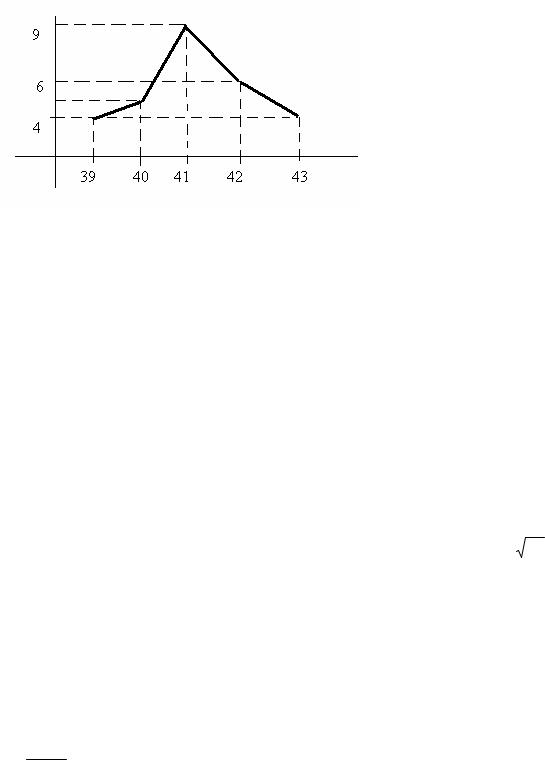
Пример 21.1. Обработать статистику – длину заготовок: 39,41,40,40, 43, 41,44, 42, 41,41,43,42,39,40,42,43,41,42,41,39,42,42,41,42,40,41,43,41,39,40.

Решение. Объем выборки 30 - выборка малая. Размах вариайий небольшой, т.к. хmin =39, xmax =43, R=5. Генеральная дискретна. Строим вариационный ряд : 39 , 40 , 41 , 42 , 43. Подсчитываем частоты : варианта 39 в статистике встретилась 4 раза; варианта 40 встретилась 5 раз; варианта 41 – 9 раз; варианта 42 – 6 раз; варианта 43 – 4 раза. Получаем статистическое распределение выборки по частотам. (левая часть таблицы ниже)

получим полигон распределения выборки по по частотам. Аналогичный полигон получится для ломаной, соединяющей точки (Xi; wi). Для статистическим распределением выборки по накопленным частотам подобная ломаная носит название кумуляты (частот или относительных частот).

Если известно статистическое распределение выборки, то можно рассматривать величину nx - число наблюдений, когда признак Х принимал значения, меньшие некоторого х. В этом случае величина w(X<x)= nx/n меняется при изменении х и потому является функцией от х. Ее называют эмпирической функцией распределения F*(x). Эта функция обладает свойствами:

0< F*(x)<1 ; F*(x).- неубывающая; F*(x)=0 при х< хmin и F*(x)=1 при х>хmax . F*(x) является полной аналогией с функцией распределения F(x).

Если выборка представлена интервальным статистическим распределением, то для геометрической ее интерпретации используют другое представление. Строят ступенчатую фигуру, ширина ступенек которой равна длине интервалов интервального вариационного ряда, а высота ступенек равна какой-нибудь частоте (или отношению частоты к ширине ступеньки – как

33

34

удобнее). Такую фигуру называют гистограммой (частот, относительных частот и т.д.). Не запрещено использовать и полигоны, взяв в качестве вариант середины интервалов (или концы интервалов).

Для примера 21.1 построим полигон частот

Комментарий. Всегда стремятся получить вариационный ряд с равноотстоящими вариантами (когда x i+1 –xi =h=const).

21.4. Расчет сводных характеристик выборки Пусть выборка представлена некоторым статистическим распределением.

Тогда приступают к расчету сводных характеристик выборки. К сводным характеристикам выборки относятся : среднее выборочное хв , выборочная дисперсия Dв и выборочное среднеквадратическое σв .

∑xini ∑xi

Комментарий. Эти две формулы фактически одна. Следует только их правильно читать. Первая из дробей подчеркивает, что варианты

сгруппированы, а вторая – варианты несгруппированы .

Зная среднее выборочное легко подсчитать выборочную дисперсию по

Эти формулы вполне просты, если варианты немногозначные или невысокоточные . Для высокоточных и-или многозначных вариант расчет по этм формулам (даже для ЭВМ) может оказаться затруднительным. В таких случаях используют специальные методы расчета сводных характеристик выборки. Особенно простым будет метод условных вариант, если вариационный ряд будет представлен равноотстоящими вариантами или интервальным распределением с постоянным шагом интервалов.

В таком случае используют переход к условным вариантам по формуле ui= xi −h C , где ui – условная (новая) варианта; С – ложный нуль (варианта Х с

34

35

превращается в целочисленный вариационный ряд, значения вариант которого не превосходят числа 7 . В самом деле, число интервалов вариационного ряда не превосходит 15. Середина ряда взята в качестве ложного нуля. А значения условных вариант всегда целые числа, т.к. для любых вариант xi=xmin+ih и

число.

Выведем соотношения, связывающие числовые характеристики условных и основных вариант. Имеем xi=h ui +C и потому

Решение. Данные вынуждают строить интервальный вариационный ряд и последующие распределения. При размахе вариаций R=1,2 и бъеме выборки n=30 разбиваем отрезок [5,0; 6,2] на 6 интервалов с шагом h=0,2. Договоримся относить узлы, совпадающие с границами интервалов к правому интервалу. Подсчитываем частоты, относительные частоты, середины интервалов.

35

36

21.5. Статистические оценки и требования к ним Как известно, для описания случайной величины (СВ) используют либо

закон ее распределения, либо числовые характеристики. Последние иногда называют параметрами распределения. Если о случайной величине известно лишь, что она подчиняется некоторому распределению и имеется статистический материал по исследованию этой СВ, то встает задача об

отыскании оценок параметров.

Определение. Статистической оценкой неизвестного параметра называют функцию от наблюдаемых значений СВ (фактически, данных эксперимента).

Для высокого качества оценки она должна удовлетворять определенным требованиям. Пусть оценивается параметр Q и в качестве оценки берется величина Q*. В таком случае :

1)оценка Q* должна быть несмещенной; (т.е. М(Q*) должно быть равно Q)

2)оценка Q* должна быть эффективной; (т.е. при заданной выборке должна иметь наименьшую дисперсию;

3)оценка Q* должна быть состоятельной; (т.е. при n → ∞ оценка должна

приближаться к оцениваемому параметру); последнее записывают так

n → ∞

Q* Æ Q

по вероятности.

Все оценки разделяют на точечные и интервальные .

21.6. Точечные оценки параметров распределения Для построения точечных оценок параметров распределения используют

либо метод моментов (Пирсона), либо метод наибольшего правдоподобия (Фишера).

О методе моментов. Если было изучено понятие момента, то центральным моментом первого порядка называют математическое ожидание. И, т.к. в качестве момента в статистике фигурирует величина хв , то для

36