1

Математика для самообразования БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ

КАФЕДРА “ВЫСШАЯ МАТЕМАТИКА”

ЮДЕНКОВ Ю.Т.

Лекции по математике технического вуза

Сводный курс. Часть 4. Теория вероятностей и математическая статистика

Пособие разработано на основе лекций, читаемых на протяжении ряда лет студентам специальности АЭП (электропривод)

по дисциплине “ Высшая математика.”

2007 г.

Введение

Часть 4 курса лекций по математике технического ВУЗа является продолжением аналогичного курса лекций часть 1, 2 и 3, которые включили в себя классические разделы математики : линейную и векторную алгебры, аналитическую геометрию, введение в математический анализ, дифференциальное исчисление функций одного и нескольких переменных, интегральное исчисление (определенный, неопределенный, несобственные, криволинейные и кратные интегралы), дифференциальные уравнения и теорию рядов, теорию функций комплексного переменного и операционное исчисление..

19.Случайные события 19.1.Предмет теории вероятностей

Всякие явления (события) рассматриваются всегда в совокупности некоторых условий. Говорят “ При выполнении таких-то условий происходит это ….”. Обозначим комплекс условий, в которых будем проводить исследования, S. В этот комплекс невозможно включить все условия – о многих мы даже не подозреваем. В таком комплексе условий происходящие события можно в некотором смысле классифицировать как : достоверные (всегда

1

2

происходят при выполнении комплекса S); невозможные (никогда не происходят при выполнении комплекса S); случайные (которые могут происходить. А могут и не происходить при выполнении комплекса S).

Теория вероятностей не ставит перед собой задачу предсказания появления некоторого события при выполнении комплекса S. Другое дело массовые случайные события. При внимательном наблюдении за многократным выполнении комплекса S можно обнаружить, что наблюдаются некоторые закономерности, которые принято называть вероятностными.

Предмет теории вероятностей – изучение закономерностей, которым подчиняются массовые случайные события.

Начала науки лежат в основе попыток создания теории азартных игр Кардано, Гюйгенсом, Блезом Паскалем, Ферма. Продолжение развития связано

сработами Муавра, Лапласа. Гаусса, Пуассона. Бурное развитие науки связано

сработами Чебышева, Маркова, Ляпунова, Бернштейна, Фишера, Колмогорова.

19.2.Вероятность случайного события

Чаще всего вместо выражения “комплекс условий S выполнен” будем говорить “проведено испытание”. Результатом испытания будет событие. События будем обозначать большими буквами латинского алфавита как точку некоторого пространства.

Полной группой событий называют набор (множество) событий , которые могут появиться в результате испытания, которые отнесены нами к интересующими нас и кроме которых ничего не может происходить.

Иначе говоря, появление одного из событий полной группы – событие достоверное.

Случайные события в свою очередь классифицируют: совместные (совместимые), которые могут появиться вместе при проведении испытания; несоместные (несовместимые), которые не могут появиться вместе; зависимые, если появление или непоявление одного из них некоторым образом влияет на появление или непоявление другого; независимые, если появление или непоявление одного из них никоимм образом не влияет на появление или непоявление другого.

Назовем каждый возможный исход испытания элементарным исходом. Взаимоисключающие друг друга элементарные исходы назовем

элементарными событиями.

Множество элементарных событий образует пространство элементарных событий.

Примеры 19.1. Подбрасывание одной монеты один раз приводит нас к пространству элементарных событий, состоящему из двух единственно возможных, исключающих друг друга событий : выпадение орла и выпадение решетки.

Подбрасывание одной игральной кости один раз приводит нас к пространству элементарных событий – выпадение 1,2,3.4,5 или 6 очков.

2

3

Подбрасывание одной монеты 2 раза приводит нас к пространству элментарных событий : два раза выпал орел, два раза выпала решка , выпал один раз орел и один раз решка.

Поступление вызовов на АТС в течение часа образует пространство элементарных событий, когда не поступает ни одного вызова до поступает число вызовов, раное мощности АТС.

Всякое случайное событие в такой постановке – это подмножество (подпространство) пространства элементарных исходов.

Пусть Ω- пространство элементарных событий. Пусть U – класс подмножеств данного множества Ω. Принято называт U – алгеброй событий.

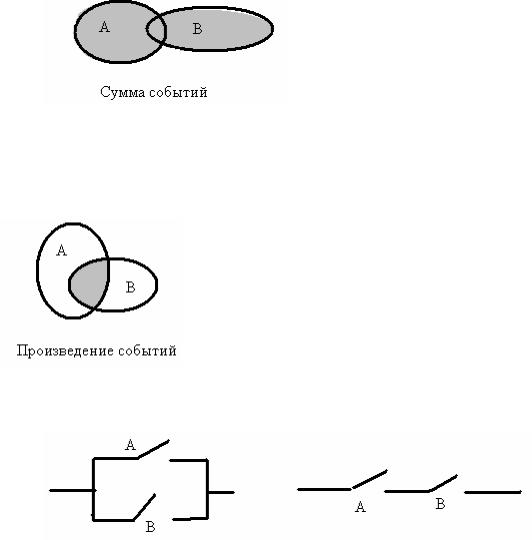
Суммой событий А и В называют событие А+В, обозначаемое С и состоящее в том, что хотябы одно их А и В произойдет. С помощью кругов Эйлера С можно изобразить как заштрихованную часть плоскости на Рис 19.1

Рис 19.1

Произведением событий А и В называют событие АВ, обозначаемое С и состоящее в том, что оба события А и В произойдут. С помощью кругов Эйлера С можно изобразить как заштрихованную часть плоскости на Рис 19.2

Рис 19.2.

Этим же рисункам соответствует электрическая (логическая) схема

Рис 19.3. Слева сумма событий; справа их произведение (замыкание цепи С и замыкание ключей А и В)

Приведенное на Рис19.3. – известные логические схемы “ и” и “или” – основа всей вычислительной техники и двоичной математики (“да” и “нет”; замкнуто и незамкнуто; 0 и 1).

3

4

Ведем для СС(случайного события) числовую характеристику. Назовем ее вероятностью случайного события и обозначим Р(А).

Классическое определение вероятности.Р(А) случайного события – это

1.0<P(A)<1 для СС. 2.Р(А)=0, если А невозможное. 3. Р(А)=1, если А достоверное(иначе Р(Ω)=1). Это аксиомы нормированности.

Примеры.19.2. Вероятность выпадения четного числа очков при однократном подбрасывании игральной кости равна 0,5 , т.к. всевозможных элементарных исходов 6, при этом возможно выпадение 2,4 и 6 – четного числа

величину w1= m1/ n1 и назовем эту величину относительной частотой появления СС А при воспроизводстве “комплекса условий S” . Воспроизведем “комплекс условий S” n2 раз и подсчитаем появление m2 раз события А. Вычислим величину w2= m2/n2 и т.д. Если этот процесс продолжить далее, то можно обнаружить, что относительная частота обладает свойством устойчивости –

изменяясь от ситуации к ситуации, значение относительной частоты принимает значения, близкие к некоторому числу. Назовем последнее статистической вероятностью случайного события (СС) А. Обозначим Р(А)=limwn .

n→∞

Отметим, что для статистической вероятности требуется хотя бы гипотетическая возможность проведения неограниченного числа испытаний – воспроизводства “комплекса условий S”.

Принцип невозможности маловероятных событий.

Если А имеет “очень малую” вероятность , то говорят, что А маловероятное событие. Это значит, что при единичном воспроизводстве “комплекса условий S” появление А почти невозможно. Термин “очень малую” вероятность взят в кавычки по той причине, что в разных практических ситуация эта вероятность может быть истолкована по разному. Например, вероятность 0,01 для опоздания поезда и для раскрытия парашюта совершенно разные вещи. Для различия таких ситуаций применяют критерий значимости высказанных предположений (гипотез). Так, при р=0,01 говорят об однопроцентном уровне

4