
- •Проектирование дискретных
- •212030, Г.Могилев, пр. Мира, 43
- •Содержание
- •1 Содержание дисциплины
- •2 Понятие дискретного автомата
- •3 Задача синтеза комбинационных дискретных автоматов
- •4 Способы задания комбинационных автоматов
- •4.1 Табличный способ (таблица истинности)
- •4.2 Числовой способ
- •4.3 Аналитический способ
- •4.4 Координатный способ (в виде карт Карно)
- •5 Способы задания дискретных автоматов с памятью
- •5.1 Таблица переходов и выходов
- •5.2 Способы задания асинхронного автомата
- •6 Задача синтеза дискретного автомата с памятью
- •7 Предоставление логических функций в базисах и-не, или-не
- •8 Понятие нормальных форм представления логических функций
- •9 Контрольная работа
- •10 Пример задачи синтеза комбинационного автомата
- •Список литературы
5.1 Таблица переходов и выходов
Таблицы переходов и выходов. При этом способе каждая функция – переходов и выходов – задается в виде таблицы, называемой, соответственно, таблицей переходов и таблицей выходов. Столбцы обеих таблиц соответствуют различным состояниям входа автомата (элементам множества {X}), строки обеих таблиц – внутренним состоянием автомата (элементам множества {S}).
На пересечении i-й строки и ј-го столбца таблицы переходов указывается то внутреннее состояние S(t+1), в которое автомат перейдет из внутреннего состояния si (i -я строка) под действием входных сигналов, соответствующих состоянию входа xј (ј-й столбец).
Поскольку S(t+1) есть значение, которое принимает функция переходов φ при X(t)= xј и S(t)= si , то, следовательно, задание S(t+1) и есть задание функции φ. На пересечении i-й строки и ј-го столбца таблицы выходов указывается то состояние выхода Z(t), которое будет иметь место, если на автомат, находящийся в момент t во внутреннем состоянии Si, входной сигнал, соответствующий состоянию входа xј.
Поскольку Z(t), есть значение функции выходов f при S(t)= si и X(t)= xј, то, следовательно, задание Z(t) это и есть задание функции f. Часто внутренние состояния автомата обозначаются не символами si, а просто цифрой i, соответствующей номеру внутреннего состояния (рисунок 7)
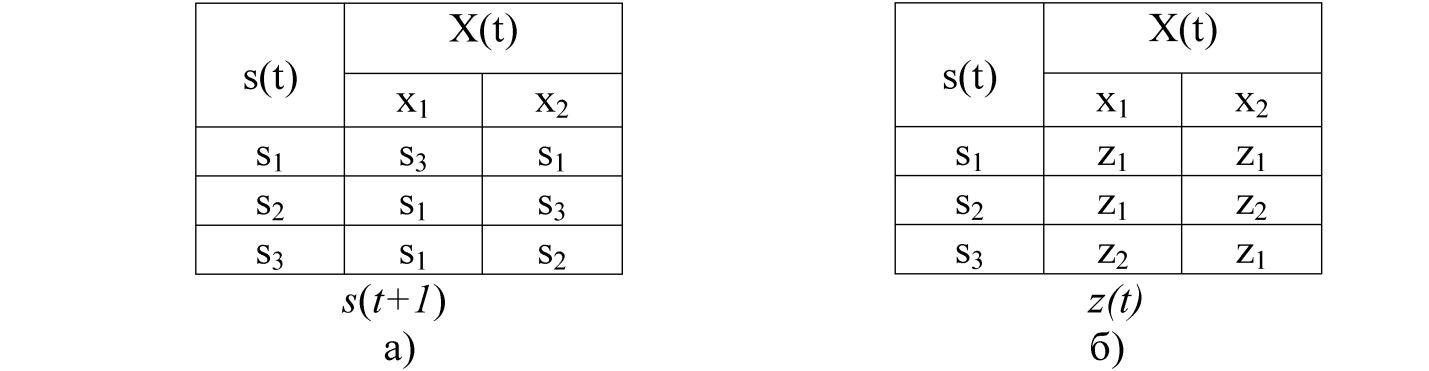
Рисунок 7 – Таблицы переходов и выходов
Таблицу переходов и выходов можно совместить в одну таблицу. Тогда записью в каждой клетке таблицы является значение функции φ в виде S(t+1), и f – в виде Z(t), которые отделяются друг от друга запятой
(рисунок 8)

Рисунок 8 – Совместная таблица переходов и выходов
Графы переходов и выходов. Граф переходов представляет собой некоторую структуру, состоящую из вершин, изображаемых кружками, и ориентированных (направленных) дуг, изображаемых в виде линий между парами вершин и снабженных стрелками, указывающими направление от одной вершины к другой. Каждая вершина графа переходов соответствует внутреннему состоянию, которое указывается внутри кружка. Направленные дуги, соединяющие две вершины i и j, отмечаются записью того состояния входа хк, который вызвал переход автомата из состояния i в состояние j, а так же записью того состояния выхода z1, которое имело место при этом. Такая двойная запись хк, z1 носит название пары «вход-выход». Например, если над дугой записано хк, z1,то это значит, что переход автомата в состояние j произошел под действием входного сигнала, соответствующего состоянию входа хк, при этом сигнал на выходе принял значение z1. В общем случае переход из состояния i в j может происходить под действием различных входных сигналов; для обозначения этого используется знак дизъюнкции «V», которым связываются все пары вход-выход, соответствующие этому переходу. Например, (х1/z1)V(x2/z2)V…V(xr/zr). Граф переходов автомата приведен на рисунке 9.

Рисунок 9 – Задание автомата в виде графа
5.2 Способы задания асинхронного автомата
Для задания асинхронного автомата можно тоже использовать таблицы и графы. Как и в синхронном автомате, строки таблицы переходов соответствуют внутренним состояниям, а столбцы – состояниям входа автомата. На пересечении строки и столбца указывается состояние автомата: устойчивое – цифрой в кружке, неустойчивое, предшествующее данному устойчивому, – той же цифрой, но без кружка. Особенностью асинхронных автоматов является то, что одному и тому же внутреннему состоянию может соответствовать несколько устойчивых состояний.
Переход из одного устойчивого состояния в другое может проходить как через неустойчивое состояние, так и непосредственно. В первом случае это связано с изменением внутреннего состояния, а во втором – нет. Это значит, что в первом случае устойчивые состояния находятся в разных строках таблицы переходов, а во втором – в одной. Кроме того, поскольку переход из одного устойчивого состояния в другое завершается при сохранении состояния входа, то неустойчивое состояние и соответствующее ему устойчивое состояние автомата всегда находятся в одном столбце таблицы переходов (рисунок 10)
Поясним рисунок 10, рассмотрев первую и вторую строки. Прежде всего, в таблице четыре строки, следовательно, автомат имеет четыре внутренних состояния: s1, s2, s3, s4, хотя устойчивых состояний у него шесть. В первой строке указано устойчивое состояние 1, которое имеет место, если автомат находится во внутреннем состоянии s1 и состояние входа есть x1. Если происходит изменение состояния входа с x1 на x2, то, следуя по строке 1 и переходя к столбцу 2, видим, что там указано неустойчивое состояние 2. Значит, автомат из состояния 1 перейдет в неустойчивое состояние 2, а затем, поскольку состояние входа сохраняется равным x2, перейдет в устойчивое состояние 2. Если затем произойдет изменение состояния входа с x2 на x3, то, двигаясь по второй строке таблицы до столбца x3, видим, что там указано устойчивое состояние 6. Это значит, что при таком изменении входа автомат из устойчивого состояния 2 в устойчивое 6 перейдет непосредственно, без изменения его внутреннего состояния. Если теперь произойдет изменение состояния входа с x3 на x4, то из таблицы определяем, что автомат перейдет в неустойчивое состояние 4 (столбец x4, вторая строка). Поскольку состояние входа x4 сохраняется до конца изменений памяти автомата, то автомат достигает устойчивого состояния 4. Чтобы завершить задание автомата, необходимо задать его функцию выходов. С этой целью строится таблица выходов, которая имеет два столбца: столбец устойчивых состояний и столбец соответствующих им выходных сигналов. Иногда таблицы выходов и переходов совмещают.

Рисунок 10 – Таблица переходов и выходов асинхронного автомата
Граф переходов асинхронного автомата по построению не отличается от синхронного, вершины его соответствуют внутренним состояниям, а направленные дуги отличаются соответствующими парами вход-выход (рисунок 11)

Рисунок 11 – Задание асинхронного автомата в виде графа
Всем устойчивым состояниям автомата соответствуют вершины с замкнутыми петлями, отмеченными теми состояниями входа, при которых, при данном внутреннем состоянии автомат будет находиться в устойчивом состоянии. Например, вершина 2 имеет петлю, отмеченную парой x2/z1 и x3/z2, как видно из таблицы, это соответствует устойчивым состояниям 2 и 6, имеющим место при втором внутреннем состоянии автомата и соответственно состоянии входа x2 и x3.
