Несобств интегр

Приближённое вычисление несобственных интегралов.

Понятие несобственного интеграла.

Понятие несобственного интеграла является обобщением понятия определённого интеграла на случай, когда либо промежуток интегрирования бесконечен, либо подынтегральная функция в некоторых точках неограниченна или неопределенна.

Различают два типа несобственных интегралов:

1. несобственные интегралы с бесконечными пределами интегрирования

2. несобственные интегралы от неограниченных функций

Опр. Если функция f(x) определена на промежутке [a; ] и при любом значении b>a существует , то можно рассмотреть , который и называют несобственным интегралом с бесконечным верхним пределом интегрирования от функции f(x) на промежутке [a; ] и обозначают .

Если данный предел конечен, то говорят что несобственный интеграл сходится, а функция f(x) интегрируема на [a; ], иначе несобственный интеграл расходится, а функция неинтегрируемая на [a; ].

Пример: сходится;

расходится

Аналогичным образом вводятся понятия несобственного интеграла с бесконечным нижним пределом и бесконечными пределами интегрирования.

Правила вычисления несобственных интегралов с бесконечными пределами интегрирования.

Так как несобственные интегралы с бесконечными пределами интегрирования по определению вычисляются предельным переходом из соответствующих определённых интегралов, то для них справедливы все свойства определённых интегралов, в частности формула Ньютона–Лейбница. Тогда, если F(x) первообразная f(x), то

Опр. Пусть функция f(x) определена на [a;b] за исключением некоторой точки в окрестности которой она неограниченна. Для определённости положим, что эта точка b. Тогда если существует то этот предел называется несобственным интегралом от неограниченной на нём функции f(x)

и обозначается

В случае, если точка с – является точкой разрыва функции f(x) на [a; b], а несобственные интегралы на отрезах [a; с] и [с; b] существуют, считают, что

Правила вычисления несобственных интегралов от неограниченных функций.

Если F(x) первообразная функции f(x) и

1) , то

2) , то

3) с– точка разрыва

Геометрический смысл несобственного интеграла.

Если существует несобственный интеграл от f(x), взятый вдоль основания криволинейной трапеции, то он задаёт площадь этой бесконечной трапеции, в противном случае понятие площади не имеет смысла.

Некоторые способы приближённого вычисления несобственных интегралов.

Существуют различные методы численного вычисления несобственных интегралов с заданной точностью.

I. Интегралы первого типа можно вычислять с помощью замены

.

Тогда несобственный интеграл перейдёт в интеграл с конечными пределами интегрирования . Интегралы такого типа можно вычислить по методу квадратур Гаусса.

II. При приближённом вычислении несобственных интегралов особая точка) можно использовать определение этих интегралов и применить метод “обрезания бесконечного предела интегрирования конечным значением”.

Интегралы соответственно представляются в виде:

,

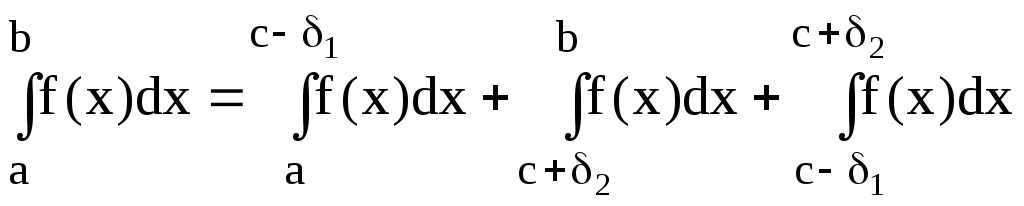
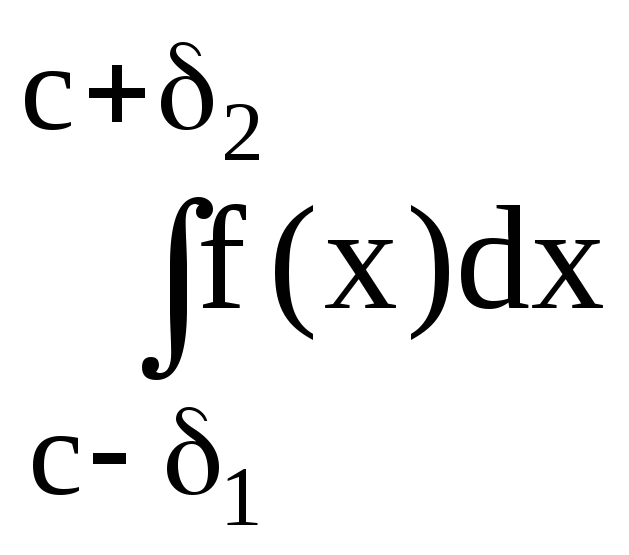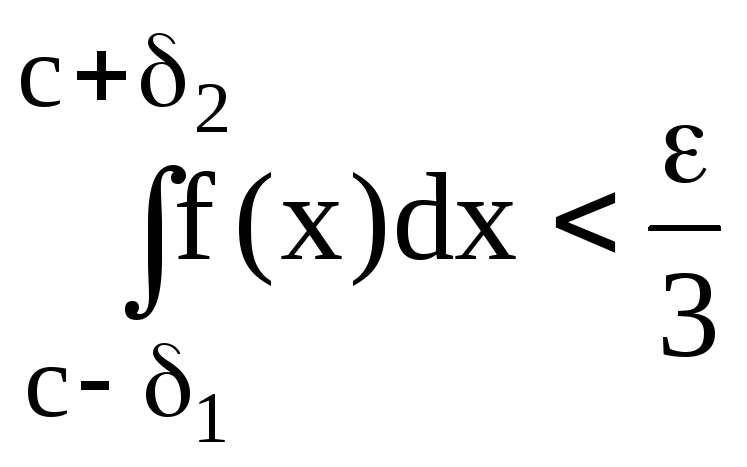причём А выбирает настолько большим, а ₁, ₂ – столь малым, чтобы в пределах заданной точности интегралы , не влияли бы на результаты, т.е. и не превосходили бы соответствующей погрешности вычислений. Остальные интегралы вычисляют уже изученными методами с соответствующими погрешностями.

Пример. Вычислить приближённо интеграл I= с точностью до 10^-4.

Решение. Из неравенства следует, что

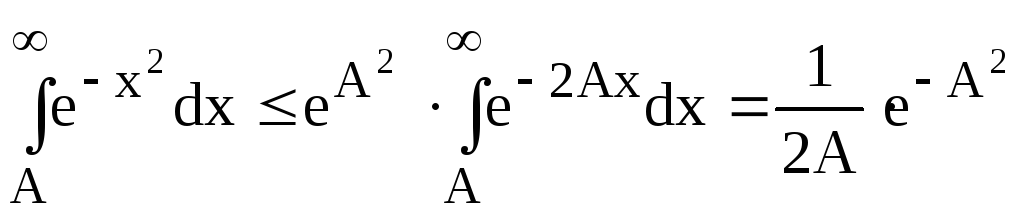. Не трудно заметить, что при подстановке вместо А значения 3 выполняется неравенство . Таким образом, достаточно взять А=3.

Значение же интеграла можно найти по формуле Симпсона с заданной точностью I=0.8862.

III. В некоторых случаях при вычислении несобственных интегралов можно использовать “мультипликативное выделение особенности”. Для этого подынтегральную функцию f(x) представляют в виде произведения двух функций , одна из которых (x) ограничена, а другая p(x) рассматривается как весовая функция – положительна и интегрируема на рассматриваемом промежутке. В данном случае полученные интегралы вычисляются с помощью квадратурных формул с весом, рассмотренных в прошлом семестре.

IV. Часто при вычислении несобственных интегралов второго типа пользуются методом выделения особенностей, предложенным Л.В. Канторовичем. Этот приём состоит в том, что если подынтегральная функция на рассматриваемом интервале ограничена , то несобственный интеграл существует и можно приступать к его вычислению. Сделать это можно с помощью аддитивного выделения особенностей. Для этого из подынтегральной функции f(x) в несобственном интеграле

выделяют в качестве слагаемого некоторую функцию g(x), имеющую те же особенности, что и f(x), легко интегрируемую и такую, чтобы разность была бы достаточно гладкой функцией.

рассмотрим достаточно широкий класс функций, имеющих вид

где для разлагается в степенной ряд

Тогда полагаем

и

Функция g(x) интегрируется непосредственно, а (x) имеет на отрезке [a; b] n непрерывных производных, а значит может быть вычислена обычными численными методами с оценкой погрешности.

Замечания: 1) Данный метод выделения особенностей может оказаться полезным при вычислении собственных интегралов, если подынтегральная функция не является достаточно гладкой.

Пример. Вычислить приближённо интеграл I=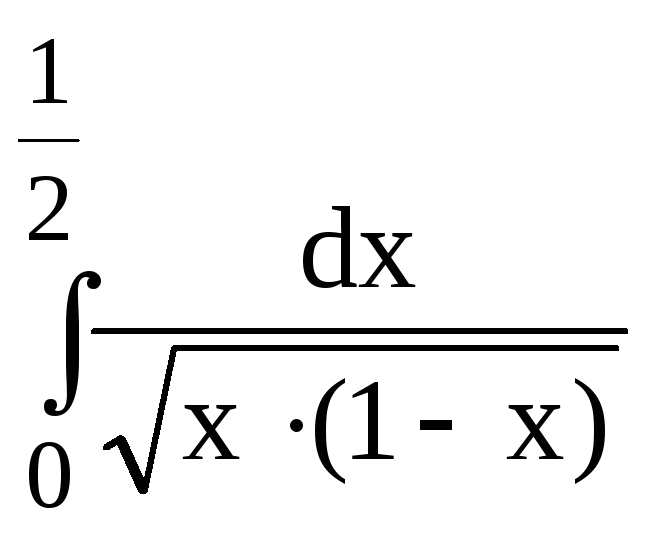

Решение. В этом интеграле особой является точка x=0.

Разложим функцию (1-x)^-1/2 по степеням x с помощью биномиального ряда

В разложении остановимся на слагаемом, содержащем x⁴, и положим

Тогда I=

Первый интеграл можно вычислить аналитически I₁=1.5691585…, а второй можно вычислить по формуле Симпсона I₁=0.00116385. В результате получаем I=1.570797.

Истинное же значение интеграла I=.