
Непрерывность функций
.doc
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»


Кафедра высшей математики
Методические указания
по изучению темы «Непрерывность функций одной переменной»
студентами бухгалтерского факультета заочной формы получения
образования (НИСПО)
Горки, 2013
Непрерывность функций одной переменной
-
Односторонние пределы
Пусть
функция
![]() определена на множестве
определена на множестве
![]() .
Введём понятие односторонних пределов
функции при
.
Введём понятие односторонних пределов
функции при
![]() .
Будем рассматривать такие значения х,
что
.
Будем рассматривать такие значения х,
что
![]() . Это означает, что
. Это означает, что
![]() ,
оставаясь всё время слева от
,
оставаясь всё время слева от
![]() .
Если при этом существует предел функции
.
Если при этом существует предел функции
![]() при
при
![]() то он называется левым
пределом
этой функции в точке
то он называется левым
пределом
этой функции в точке
![]() ( или при
( или при
![]() )
и обозначается
)
и обозначается
![]() .
.
Пусть
теперь
![]() ,
оставаясь всё время справа от
,
оставаясь всё время справа от
![]() ,
т.е. оставаясь больше
,
т.е. оставаясь больше
![]() .
Если при этом существует предел функции
.
Если при этом существует предел функции
![]() ,
то он называется правым
пределом
этой функции в точке
,
то он называется правым
пределом
этой функции в точке
![]() и обозначается
и обозначается
![]() .
.
Левый и правый пределы называются односторонними пределами функции в точке.
Если существуют односторонние пределы функции в точке и они равны между собой, то функция имеет тот же предел в этой точке:
![]()
![]()
![]() .
.
Если
односторонние пределы функции в точке
![]() существуют, но не равны между собой, то
предел функции в этой точке не существует.
существуют, но не равны между собой, то
предел функции в этой точке не существует.
-
Непрерывность функции в точке
Пусть
функция
![]() определена
на некотором множестве D.
Пусть независимая переменная х
переходит от одного своего (начального)
значения
определена
на некотором множестве D.
Пусть независимая переменная х
переходит от одного своего (начального)
значения
![]() к другому (конечному) значению
к другому (конечному) значению
![]() .
Разность
конечного и начального значений
называется приращением
величины х
и обозначается
.
Разность
конечного и начального значений
называется приращением
величины х
и обозначается
![]() .
Приращение может быть как положительным,
так и отрицательным. В первом случае
величина х
при переходе от
.
Приращение может быть как положительным,
так и отрицательным. В первом случае
величина х
при переходе от
![]() к х
увеличивается, а во втором случае -
уменьшается.
к х
увеличивается, а во втором случае -
уменьшается.
Если
независимая переменная х
получает некоторое приращение
![]() ,
то функция
,
то функция
![]() получает приращение
получает приращение
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Приращением
функции
![]() в
точке
в
точке
![]() называется разность
называется разность
![]() ,
где
,
где
![]() – приращение независимой переменной.
– приращение независимой переменной.
Можно дать несколько определений непрерывности функции в точке.
-
Функция
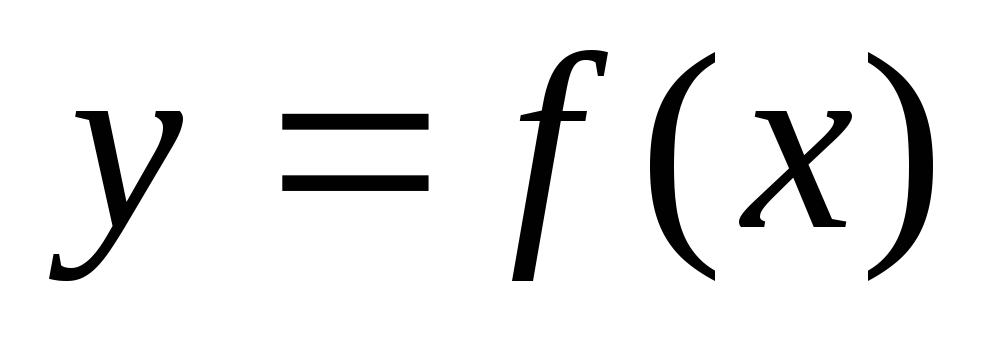 называется
непрерывной
в
точке
называется
непрерывной
в
точке
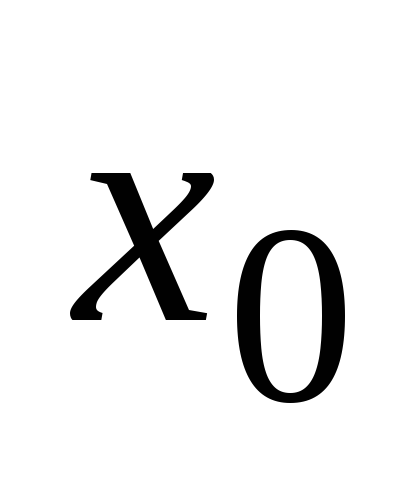 ,
если она определена в окрестности точки
,
если она определена в окрестности точки
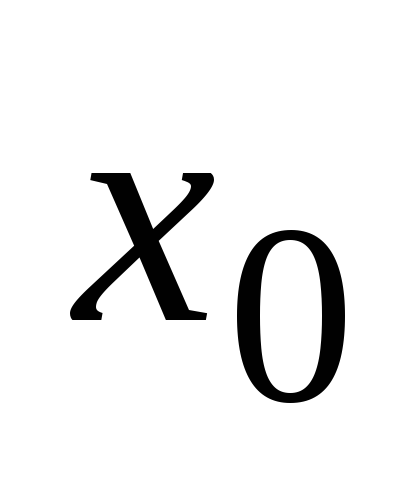 и
и
 т.е.
т.е.
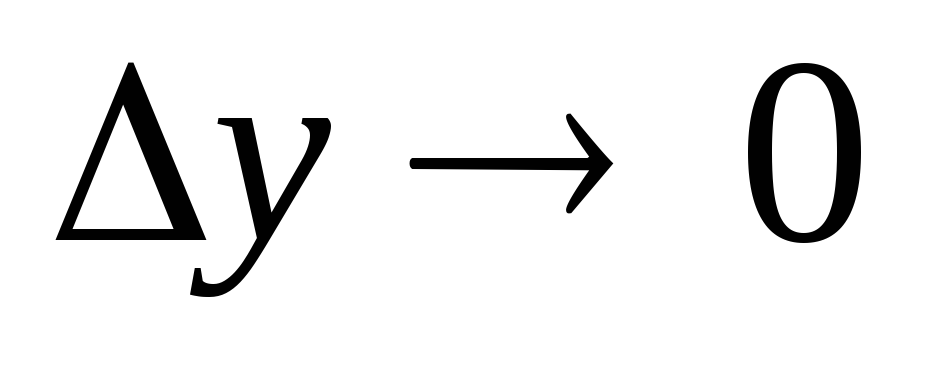 при
при
 .
Это означает, что функция непрерывна
в токе
.
Это означает, что функция непрерывна
в токе
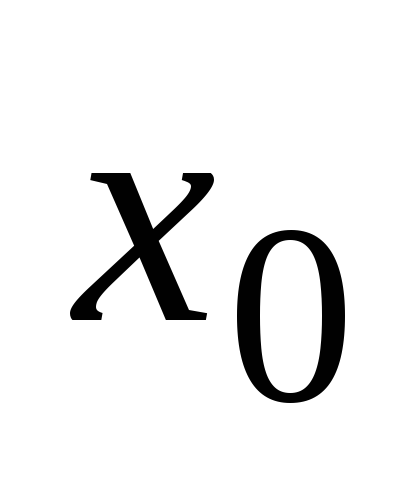 ,
если она определена в окрестности этой
точки и если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.
,
если она определена в окрестности этой
точки и если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции. -
Функция
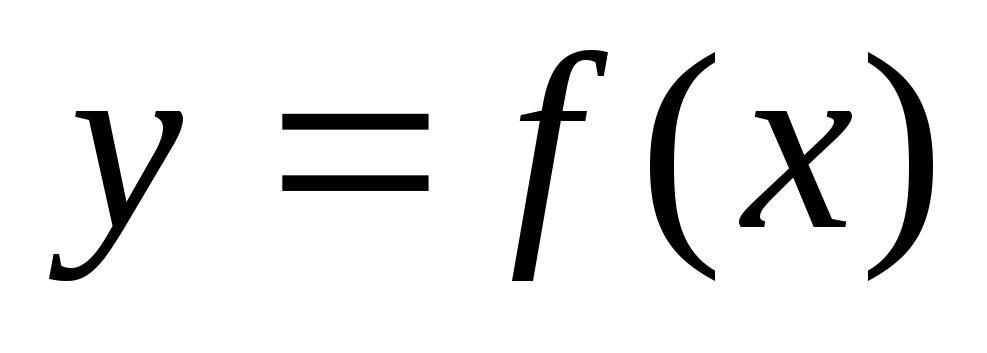 называется непрерывной
в
точке
называется непрерывной
в
точке
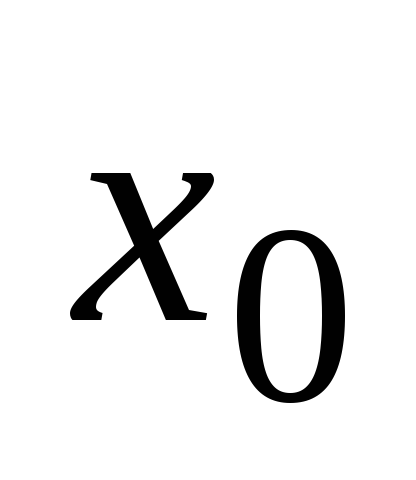 ,
если предел функции при
,
если предел функции при
 равен значению функции в этой точке:
равен значению функции в этой точке:
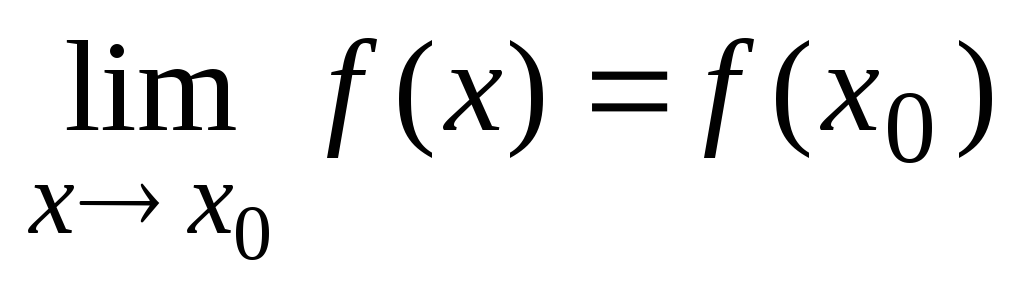 .
.

-
Функция
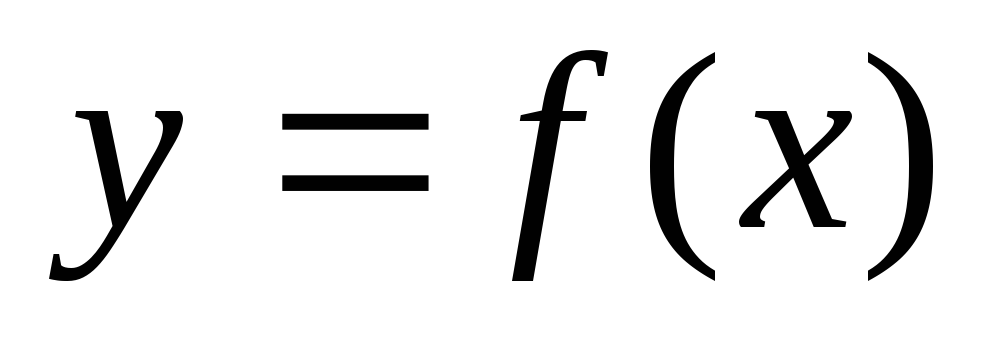 называется непрерывной
в точке
называется непрерывной
в точке
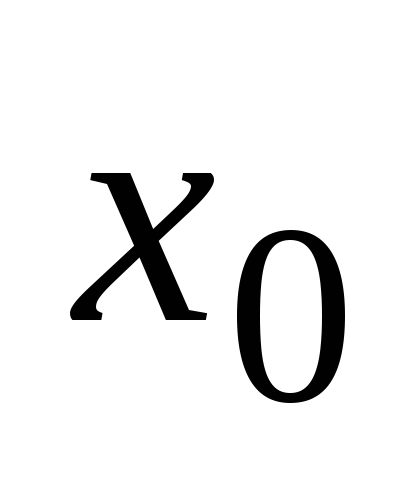 ,
если существуют левый и правый пределы
этой функции при
,
если существуют левый и правый пределы
этой функции при
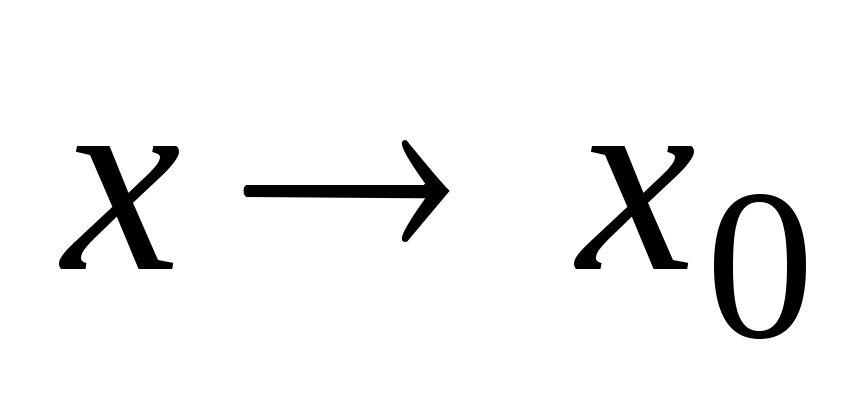 и если эти пределы равны между собой
и равны значению функции в этой точке:
и если эти пределы равны между собой
и равны значению функции в этой точке:
![]() .
.
Функция
называется непрерывной
в интервале,
если она непрерывна в каждой точке этого
интервала. Геометрически непрерывность
функции
![]() в замкнутом интервале означает, что
график функции представляет собой
сплошную линию без разрывов.
в замкнутом интервале означает, что
график функции представляет собой
сплошную линию без разрывов.
Непрерывные на отрезке функции обладают важными свойствами, которые выражаются следующими утверждениями.
![]() Если
функция
Если
функция
![]() непрерывна
на отрезке [a,
b],
то она ограничена на этом отрезке.
непрерывна
на отрезке [a,
b],
то она ограничена на этом отрезке.
![]() Если
функция
Если
функция
![]() непрерывна
на отрезке [a,
b],
то она достигает на этом отрезке своего
наименьшего и наибольшего значений.
непрерывна
на отрезке [a,
b],
то она достигает на этом отрезке своего
наименьшего и наибольшего значений.
![]() Если
функция
Если
функция
![]() непрерывна
на отрезке [a,b]
и
непрерывна
на отрезке [a,b]
и
![]() ,
то каким бы ни было число С,
заключённое между числами А
и В,
найдётся точка
,
то каким бы ни было число С,
заключённое между числами А
и В,
найдётся точка
![]() ,
что
,
что
![]() .
.
Из
этого утверждения следует, что если
функция
![]() непрерывна на [a,
b]
и на концах этого отрезка принимает
значения разных знаков, то на этом
отрезке существует хотя бы одна точка
c,
в которой функция обращается в нуль.
непрерывна на [a,
b]
и на концах этого отрезка принимает
значения разных знаков, то на этом
отрезке существует хотя бы одна точка
c,
в которой функция обращается в нуль.
Справедливо следующее утверждение: если над непрерывными функциями производить арифметические действия, то в результате получается непрерывная функция.
Пример 1. Исследовать на непрерывность функцию
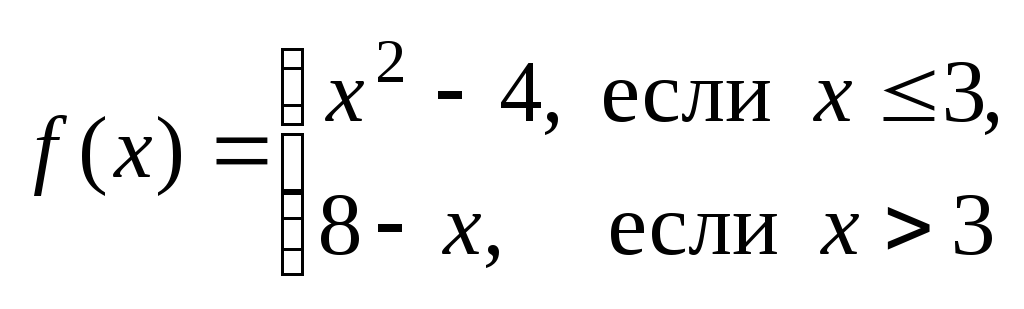 в
точке
в
точке
![]() .
.
Решение.
Значение функции при
![]() есть
есть
![]() .
Вычислим односторонние пределы функции
в точке
.
Вычислим односторонние пределы функции
в точке
![]() :
:
![]() ,
,
![]() .
.
Так
как односторонние пределы при
![]() равны между собой и равны значению
функции в этой точке, то данная функция
непрерывна в точке
равны между собой и равны значению
функции в этой точке, то данная функция
непрерывна в точке
![]() .
.
3. Непрерывность элементарных функций
Рассмотрим
функцию
![]() .
Эта постоянная функция непрерывна в
любой точке
.
Эта постоянная функция непрерывна в
любой точке
![]() ,
так как
,
так как
![]() .
.
Функция
![]() также непрерывна в каждой точке
также непрерывна в каждой точке
![]() ,
так как
,
так как
![]() .
Так как
.
Так как
![]() ,
то на основании приведённого утверждения
об арифметических операциях над
непрерывными функциями
,
то на основании приведённого утверждения
об арифметических операциях над
непрерывными функциями
![]() будет непрерывной. Непрерывными будут
такжен функции
будет непрерывной. Непрерывными будут
такжен функции
![]() .
.
Аналогично можно показать непрерывность остальных элементарных функций.
Таким образом, любая элементарная функция непрерывна в своей области определения, т.е. область определения элементарной функции совпадает с областью её непрерывности.
-
Непрерывность сложной и обратной функций
Пусть
функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
а функция
,
а функция
![]() непрерывна в точке
непрерывна в точке
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() непрерывна в точке
непрерывна в точке
![]() .
Это означает, что если сложная функция
составлена из непрерывных функций, то
она также будет непрерывной, т.е.
непрерывная
функция от непрерывной функции есть
функция непрерывная.
Это определение распространяется на
конечное число непрерывных функций.
.
Это означает, что если сложная функция
составлена из непрерывных функций, то
она также будет непрерывной, т.е.
непрерывная
функция от непрерывной функции есть
функция непрерывная.
Это определение распространяется на
конечное число непрерывных функций.
Из этого определения следует, что под знаком непрерывной функции можно переходить к пределу:
![]() .
.
Это означает, что если функция непрерывна, то знак предела и знак функции можно поменять местами.
Пусть
функция
![]() определена, строго монотонна и непрерывна
на отрезке [a,
b].
Тогда обратная ей функция
определена, строго монотонна и непрерывна
на отрезке [a,
b].
Тогда обратная ей функция
![]() определена, строго монотонна и непрерывна
на отрезке [A,
B],
где
определена, строго монотонна и непрерывна
на отрезке [A,
B],
где
![]() .
.
-
Точки разрыва и их классификация
Как
уже известно, что если функция
![]() определена на множестве D
и в точке
определена на множестве D
и в точке
![]() выполняется условие
выполняется условие
![]() ,
то функция непрерывна в этой точке. Если
же это условие непрерывности не
выполняется, то в точке х0
функция имеет разрыв.
,
то функция непрерывна в этой точке. Если
же это условие непрерывности не
выполняется, то в точке х0
функция имеет разрыв.
Точка
![]() называется точкой
разрыва первого рода
функции
называется точкой
разрыва первого рода
функции
![]() ,
если в этой точке функция имеет конечные
односторонние пределы, не равные друг
другу, т.е.
,
если в этой точке функция имеет конечные
односторонние пределы, не равные друг
другу, т.е.
![]() .
При этом величина
.
При этом величина
![]()
называется
скачком
функции
![]() в точке
в точке
![]() .
.

Точка
![]() называется точкой
устранимого разрыва
функции
называется точкой
устранимого разрыва
функции
![]() ,
если односторонние пределы функции в
этой точке равны друг другу и не равны
значению функции в этой точке, т.е.
,
если односторонние пределы функции в
этой точке равны друг другу и не равны
значению функции в этой точке, т.е.
![]() В
этом случае для устранения разрыва в
точке
В
этом случае для устранения разрыва в
точке
![]() нужно положить
нужно положить
![]()
Точка
х0
называется точкой
разрыва второго рода
функции
![]() если
хотя бы один из односторонних пределов
если
хотя бы один из односторонних пределов
![]() или
или
![]() в этой точке либо не существует, либо
равен бесконечности.
в этой точке либо не существует, либо
равен бесконечности.
Пример 2. Исследовать на непрерывность функцию
![]() .
.
Решение.
Функция определена и непрерывна на всей
числовой прямой, за исключением точки
![]() .
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции в точке
.
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции в точке
![]() :
:
![]() ,
,
![]() .
.
Так
как в точке
![]() односторонние пределы равны между
собой, а функция в этой точке не определена,
то точка
односторонние пределы равны между
собой, а функция в этой точке не определена,
то точка
![]() является точкой устранимого разрыва.
Чтобы устранить разрыв в этой точке,
необходимо доопределить функцию, положив
является точкой устранимого разрыва.
Чтобы устранить разрыв в этой точке,
необходимо доопределить функцию, положив
![]() .
.
Пример 3. Исследовать на непрерывность функцию
![]() .
.
Решение.
Функция определена и непрерывна на всём
множестве действительных чисел, кроме
![]() .
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции при
.
В этой точке функция имеет разрыв. Найдём
односторонние пределы функции при
![]() :
:
![]() ,
,
![]() .
.
Так
как данная функция в точке
![]() имеет конечные односторонние пределы,
не равные друг другу, то эта точка
является точкой разрыва первого рода.
Скачок функции в точке
имеет конечные односторонние пределы,
не равные друг другу, то эта точка
является точкой разрыва первого рода.
Скачок функции в точке
![]() равен
равен
![]() .
.
Вопросы для самоконтроля знаний
-
Что называется приращением аргумента и приращением функции?
-
Что называется левосторонним (левым) пределом функции?
-
Что называется правосторонним (правым) пределом функции?
-
Какая функция называется непрерывной в точке, в интервале?
-
Какая точка называется точкой разрыва функции?
-
Какая точка называется точкой разрыва первого рода?
-
Какая точка называется точкой разрыва второго рода?
-
Какая точка называется точкой устранимого разрыва?
Задания для самостоятельной работы
Исследовать функции на непрерывность:
-
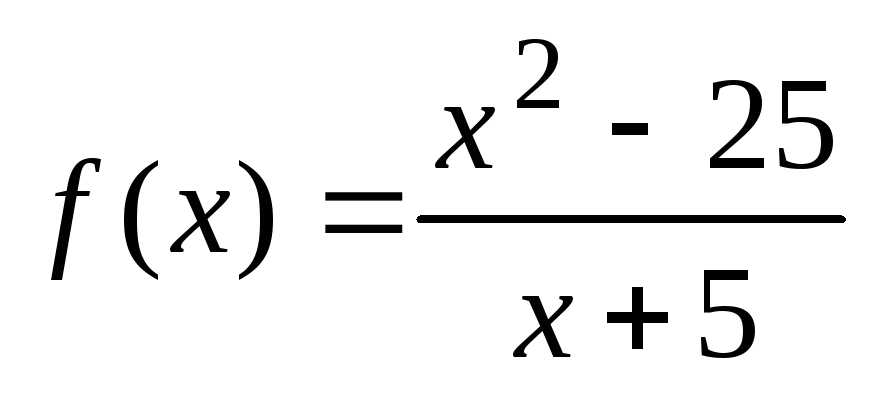 ;
2)
;
2)
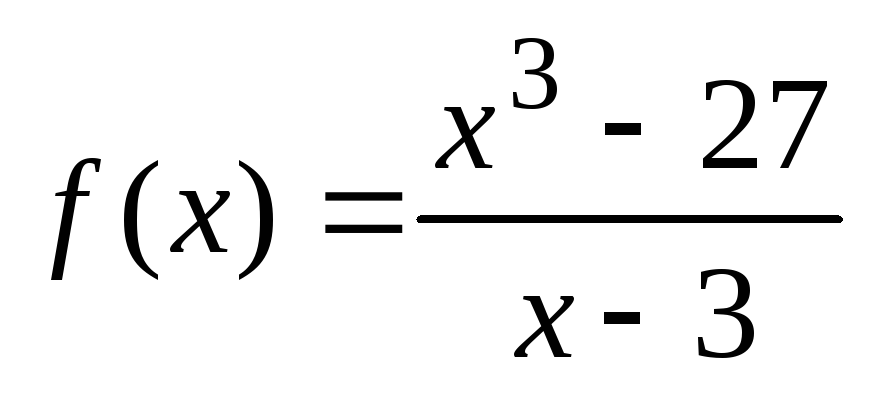 ;
3)
;
3)
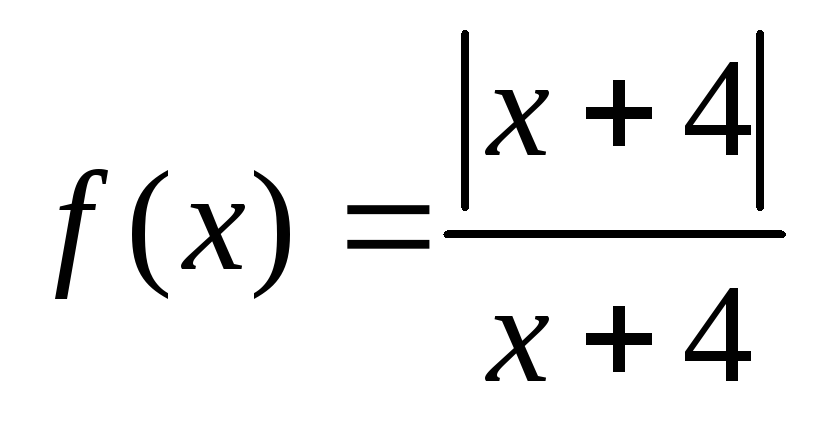 ;
;
![]() в
точке
в
точке
![]() .
.
