Численное интегрирование1

Численное интегрирование.

Известно, что определённый интеграл можно вычислить по формуле Ньютона –Лейбница, выражая через неопределённый интеграл. Однако класс интегрируемых функций довольно узкий.

Например – нельзя отнести к классу интегрируемых. Поэтому при вычислении определённых интегралов важную роль играют численные, приближённые методы интегрирования.

Кроме того, часто приходится интегрировать функции заданные таблично. В данном случае, как правило, используется интерполяция подынтегральной функции, а лишь затем осуществляется аналитическое интегрирование. Такой способ численного интегрирования даёт достаточно точные результаты при условии, что исходная функция заведомо гладкая.

Однако подынтегральная функция на промежутке интегрирования может иметь некоторые особенности. Так, например, могут существовать точки, в которых функция имеет резко изменяющиеся или разрывные производные внутри промежутка интегрирования. В этом случае мы должны заранее освободиться от таких особенностей. Делается это путём разложения подынтегральной функции на 2 сомножителя, т.е. представление интеграла в виде

где [a; b] – любой конечный или бесконечный отрезок числовой оси; р(х) – весовая функция, учитывающая особенности поведения подынтегральной функции; f(x) – произвольная гладкая функция.

Данная формула называется квадратурной формулой.

Квадратурная сумма и связанные с ней задачи.

Интеграл можно с определённой долей погрешности представить в виде , для x_k принадлежащих [a; b].

Такое представление определённого интеграла называется квадратурной суммой, а её параметры соответственно A_k – квадратурными коэффициентами, x_k – квадратурными узлами. Квадратурная сумма однозначно определяется 2n+1 параметром: n значений А_к, n значений х_k и сам параметр n.

Т.к. точность вычисления интеграла зависит от числа разбиений n, то значение n должно быть достаточно велико. Остальные же параметры подбираются так, чтобы функция при интегрировании давала наилучшее приближение для класса функций f(x).

При выборе параметров квадратурной суммы поступают следующим образом. Если функция f(x) известна или задана таблицей значений f(x_k) в некоторой системе узлов x_k k= и на выбор коэффициентов не налагаются дополнительные ограничения, то используют интерполяционные квадратурные формулы. Основой для таких формул служат интерполяционные многочлены Лагранжа.

1. По узловым точкам строится интерполяционный многочлен Лагранжа:

,

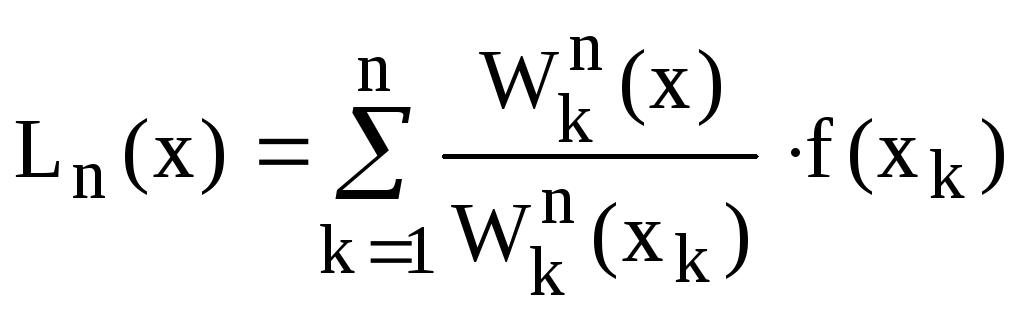где

2. Считая f(x)=L_n(x), получаем

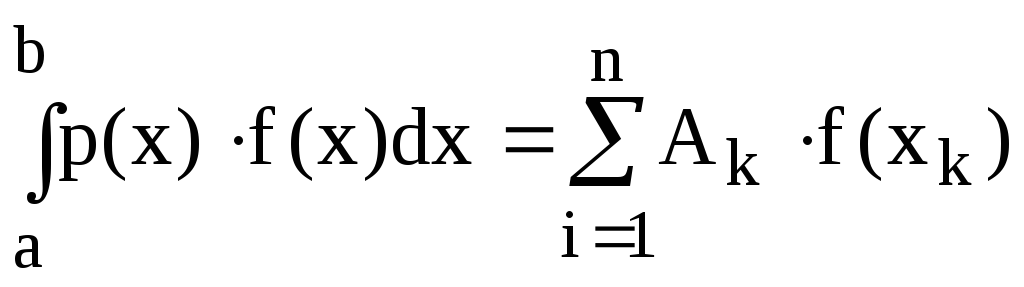
где – интеграл от интерполяционного многочлена Лагранжа.

Квадратурные формулы , у которых коэффициенты A_k определяются данным способом называются интерполяционными.

Квадратурные формулы с равноотстоящими узлами (формулы Ньютона – Котеса).

Квадратурные формулы с равноотстоящими узлами применяются для вычисления интеграла

с постоянной весовой функцией (p(x)1) и конечным отрезком интегрирования [a; b]. Для этого случая квадратурная формула может быть переписана в виде

(*)

где ;

.

Квадратурные формулы называются формулами Ньютона­­–Котеса. Установлено, что при большом n (числе разбиения) в формуле Ньютона­­–Котеса небольшие погрешности в значениях функции могут приводить к значительным погрешностям в квадратурной сумме. Поэтому для большого n данная формула редко используется при вычислениях.

Однако в численном интегрировании большее распространение получили частные случаи формулы Ньютона – Котеса – формулы трапеций и парабол (Симпсона).

Формула трапеций.

Положим в формуле (*) n=1. Получим

Так как применение этой формулы для одного интервала приведёт к заведомо большой погрешности то для её уменьшения предварительно разбивают отрезок [a; b] на достаточно большое число интервалов и к каждому из них применяют приведенную выше формулу.

Разбивая отрезок [a; b] на n равных частей длины h=(b-a)/n и применяя формулу трапеций к частичному отрезку [a+kh; a(k+1)h], a затем суммируя по всем частичным отрезкам получим так называемую общую формулу трапеций

,

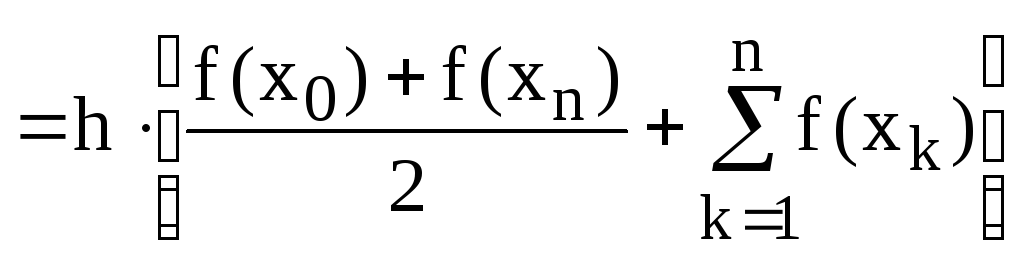где h=(b-a)/n;

n–число разбиений;

x₀=a, x_k=a+hk, x_n=b.

Формула парабол (Симпсона).

При n=2 в формуле (*) получим

Поступая аналогично с рассмотренным выше случаем для каждого удвоенного частичного отрезка [a; a+2h], [ a+2h; a+4h ] и т.д., получаем

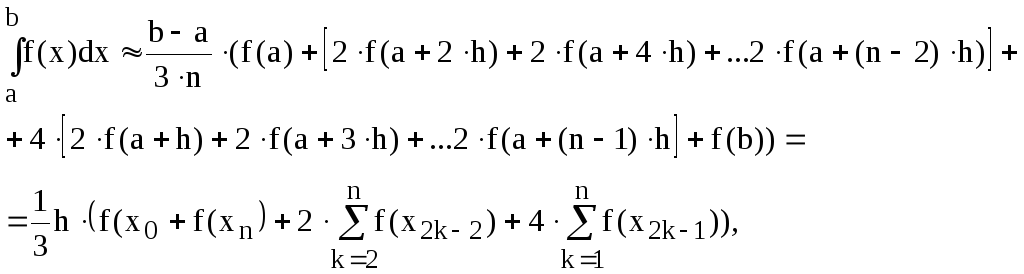
где h=(b-a)/n;

n–число разбиений;

x₀=a, x_k=a+hk, x_n=b.

Данную приближённую формулу называют общей формулой Симпсона.

С геометрической точки зрения применение формул трапеций и парабол (Симпсона) означает замену графика подынтегральной функции на каждом частичном интервале соответственно прямой и параболой. Тем самым вычисление площади криволинейной трапеции, ограниченной графиком функции у=f(x) и пределами интегрирования (прямыми x=a, x=b) мы подменяем на вычисление площади фигуры, составленной из простейших, площадь которых легко считается.

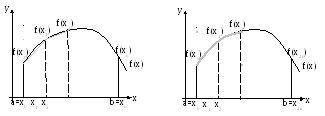
Оценка погрешностей квадратурных формул.

Остаточный член квадратурных формул равен

.

Если f(x) имеет непрерывную производную порядка n, то остаток интерполяционной квадратуры может быть представлен в виде

.

Тогда

где M_n

Для формулы трапеций, при условии что непрерывна на [a; b]

где M₂=.

Для формулы Симпсона, при условии что непрерывна на [a; b]

где M₄=.