Векторы в n-мерном пространстве

Учреждение образования «Белорусская государственная

сельскохозяйственная академия»

Кафедра высшей математики

Методические указания

по изучению темы «Векторы в n-мерном пространстве» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)

Горки, 2013

Векторы в n-мерном пространстве

1. n-мерные арифметические векторы

n-мерным арифметическим вектором называется упорядоченная совокупность n действительных чисел, а числа, входящие в эту совокупность, называются координатами вектора.

Число координат вектора называется его размерностью.

Если все координаты вектора равны нулю, то вектор называется нулевым и обозначается 0 или .

Если соответствующие координаты векторов и равны, то векторы называются равными:

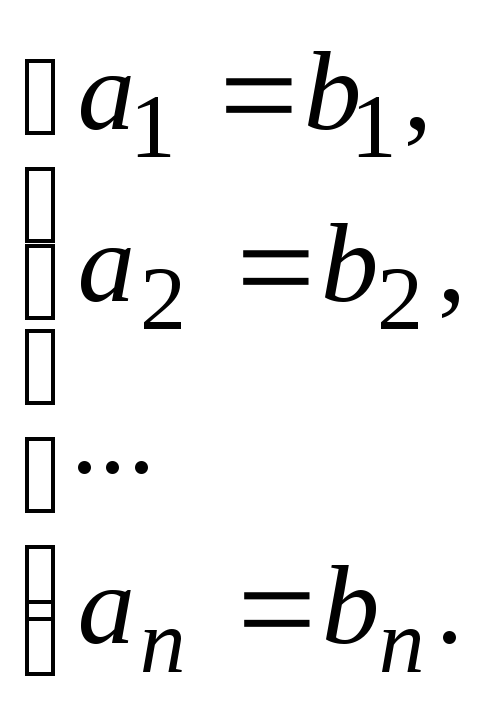
Наиболее простыми операциями над n-мерными векторами являются сложение векторов, вычитание векторов и умножение вектора на число. Такие операции называются линейными. Складывать и вычитать можно векторы только одинаковой размерности.

Суммой (разностью) двух n-мерных векторов и называется n-мерный вектор

и обозначается .

Произведением n-мерного вектора на число называется n-мерный вектор

.

Таким образом, при сложении или вычитании векторов складываются или вычитаются их одноименные координаты. При умножении вектора на число каждая координата вектора умножается на это число.

Множество всех n-мерных векторов с введёнными на нём операциями сложения, вычитания и умножения вектора на число называется n-мерным арифметическим векторным пространством и обозначается .

2. Линейная зависимость векторов

Пусть имеется m n-мерных векторов и m действительных чисел . Выражение

называется линейной комбинацией векторов , а числа называются коэффициентами линейной комбинации.

Линейная комбинация n-мерных векторов также является n-мерным вектором.

Векторы называются линейно зависимыми, если существуют такие числа , из которых хотя бы одно отлично от нуля, что выполняется равенство

.

Если данное равенство возможно лишь в случае, когда все числа равны нулю, то векторы называются линейно независимыми.

Рассматриваемые векторы называются системой векторов.

Если некоторый вектор может быть представлен в виде линейной комбинации векторов т.е.

,

то расширенная система векторов будет линейно зависимой. И, наоборот, если система векторов линейно зависима, то один из векторов системы может быть представлен в виде линейной комбинации остальных.

Таким образом, условие линейной зависимости векторов можно сформулировать следующим образом: система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов системы является линейной комбинацией остальных векторов.

3. Базис и ранг системы векторов

Пусть дана система векторов . Базисом данной системы векторов (максимальной линейно независимой подсистемой) называется такая подсистема, векторы которой линейно независимы, а любой другой вектор системы является их линейной комбинацией.

Система векторов может иметь несколько базисов. При этом все они содержат одинаковое количество векторов.

Рангом системы векторов называется число векторов в любом базисе системы. Другими словами, ранг системы векторов равен максимальному числу линейно независимых векторов системы.

Базисом n-мерного векторного пространства называется совокупность n линейно независимых векторов этого пространства.

4. Разложение вектора по системе векторов

Пусть имеется система векторов , принадлежащих пространству , и произвольный вектор :

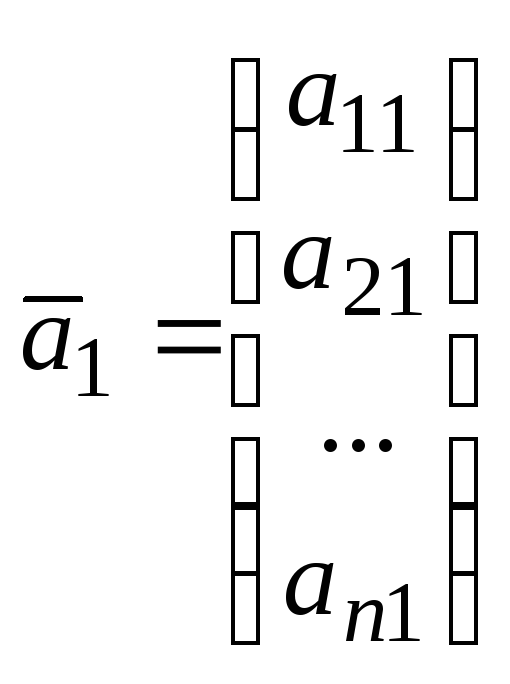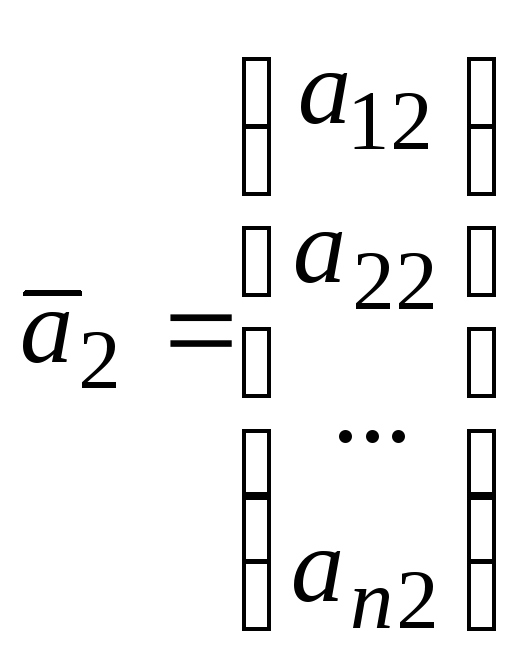, , …, , . Представим вектор в виде линейной комбинации векторов :

.

Такая запись называется разложением вектора по векторам . В связи с этим возникает вопрос: всегда ли можно произвольный вектор разложить по векторам этого же пространства?

Запишем данную линейную комбинацию в виде:

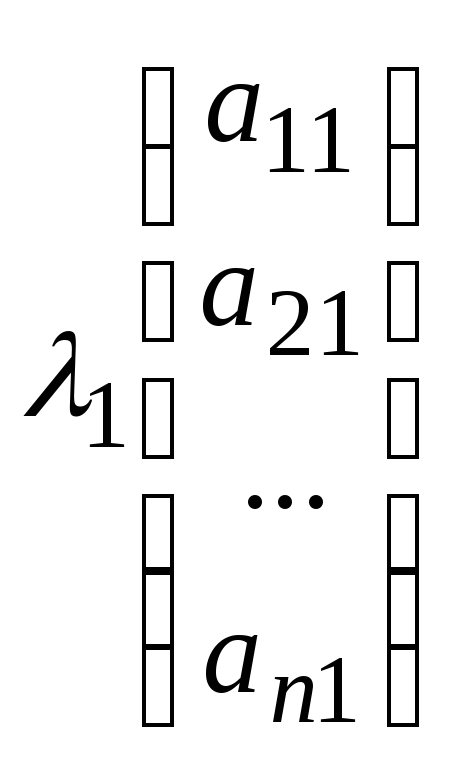++…+=, или

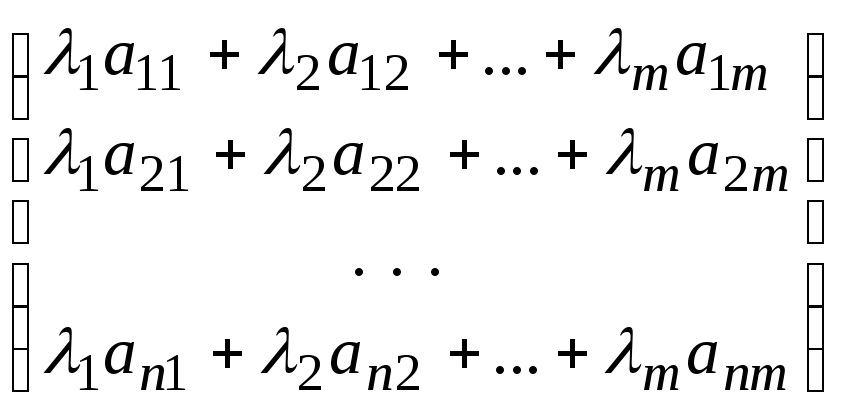=, или

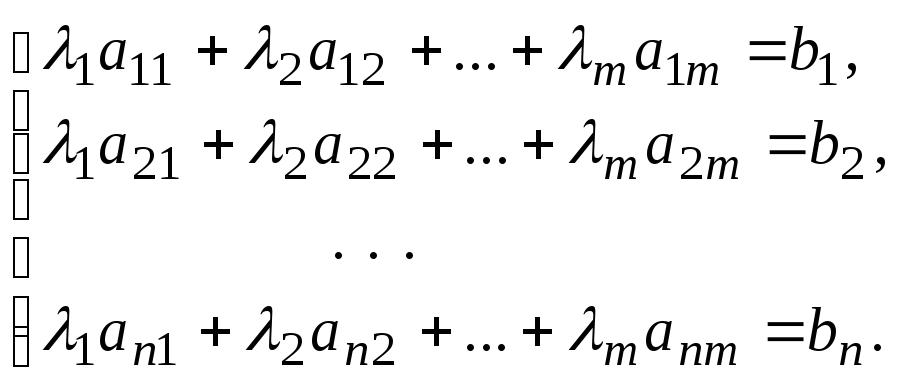
Получена система n уравнений с m переменными . Если данная система имеет единственное решение, то вектор единственным образом может быть разложен по векторам . В этом случае называются коэффициентами разложения вектора по векторам . Если полученная система решений не имеет, то вектор не может быть разложен по векторам . Если же система имеет бесчисленное множество решений, то вектор может быть разложен по векторам множеством различных способов.

Таким образом, представление вектора в виде линейной комбинации системы векторов равносильно решению системы линейных уравнений.

Пусть векторы представляют собой некоторый базис n-мерного векторного пространства. Тогда любой вектор этого пространства может быть разложен по векторам базиса и притом единственным образом.

Пример 1. Даны векторы , и , образующие базис трёхмерного векторного пространства. Разложить вектор по этому базису.

Решение. По условию задачи вектор нужно представить в виде линейной комбинации векторов , т.е. или . Последнее равенство запишем в виде

, или

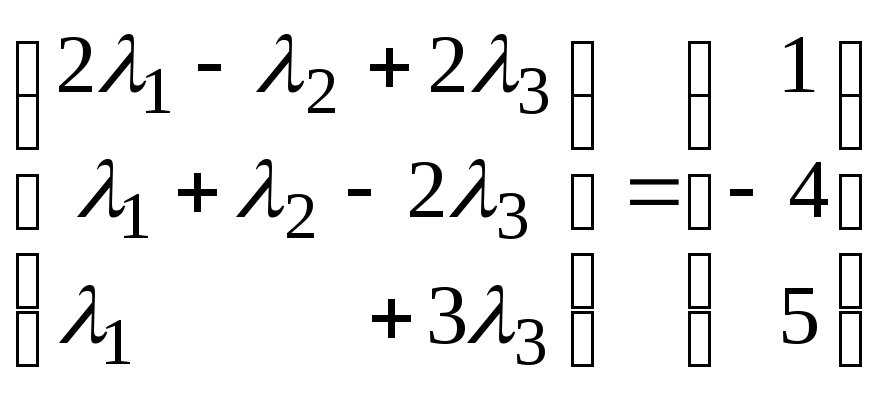, или

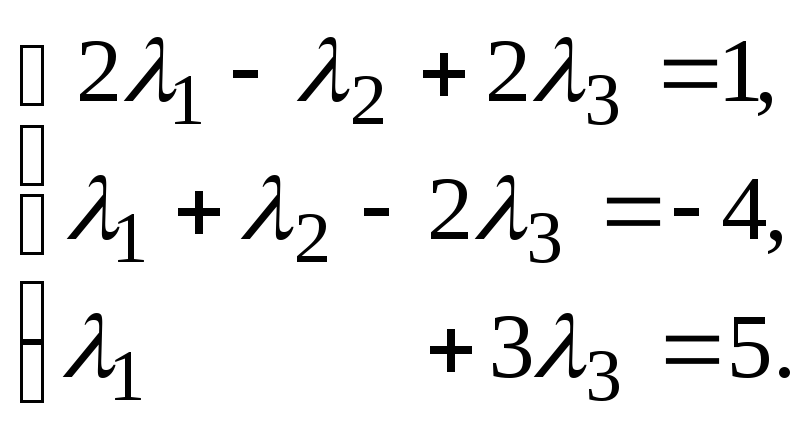
Получена система трех уравнений с тремя переменными . Решив данную систему, получим . Таким образом, .

Вопросы для самоконтроля знаний

1. Что называется n-мерным арифметическим вектором?

2. Как определяется сумма, разность двух n-мерных векторов и произведение n-мерного вектора на скаляр?

3. Что такое линейная комбинация m векторов?

4. Какая система векторов называется линейно зависимой и линейно независимой?

5. Что понимают под разложением вектора по системе векторов?

6. Что называется базисом системы векторов и базисом пространства?

Задания для самостоятельной работы

1. Даны векторы , образующие базис двумерного пространства. Разложить вектор по этому базису.

2. Разложить вектор 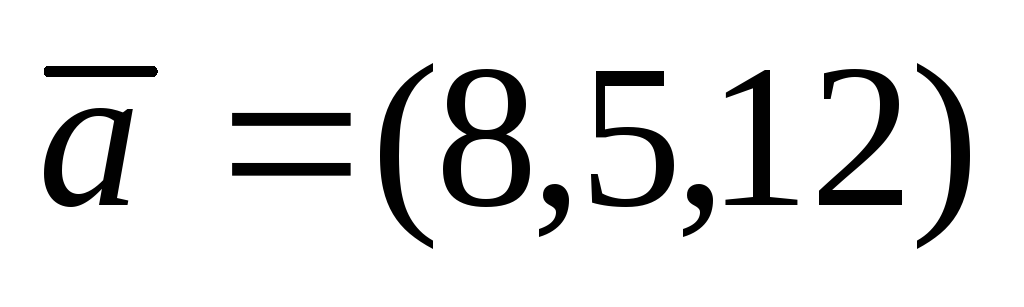по базису .

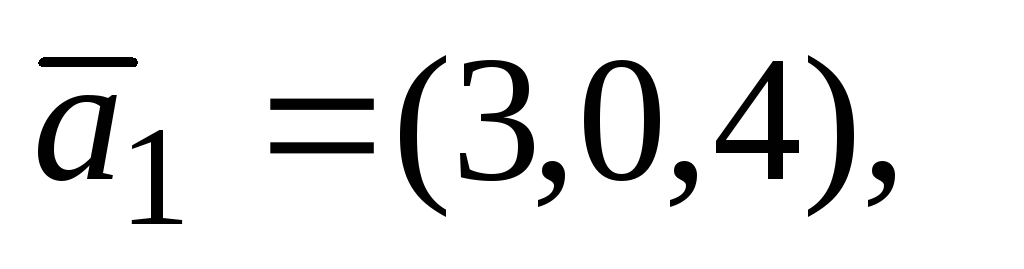
8