-
Прямая линия в пространстве
С
любой прямой в пространстве связан
вектор, который лежит на данной прямой
или на ей параллельной. Такой вектор
называется направляющим
вектором прямой
и обозначается
.
Параметрическими
уравнениями прямой,
проходящей через точку
,
называются уравнения
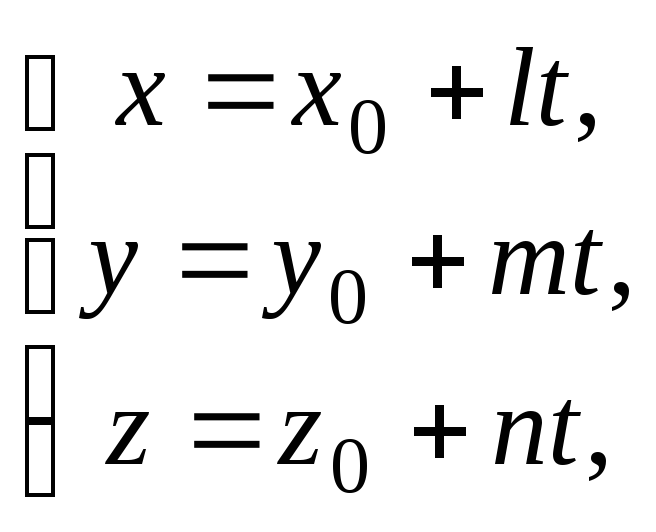
где l, m, n – координаты направляющего вектора, t - параметр.
Исключим из этих уравнений параметр t :
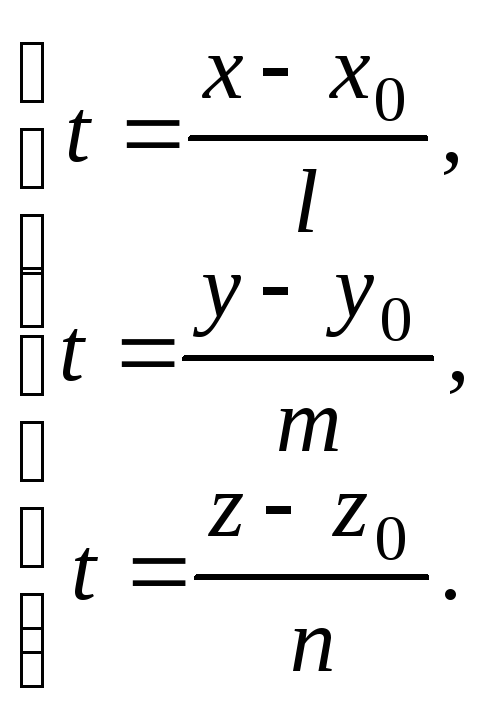
На основании этого можно записать
.
Полученные уравнения называются каноническими уравнениями прямой.
Пусть
заданы точки
и
.
Уравнение
прямой, проходящей через две точки,
имеет вид:
.
Пример
12.
Составить параметрические и канонические
уравнения прямой, проходящей через
точку
параллельно вектору
.
Решение.
По условию
,
,
,
,
,
.
Подставим
в параметрические и канонические
уравнения прямой и получим:
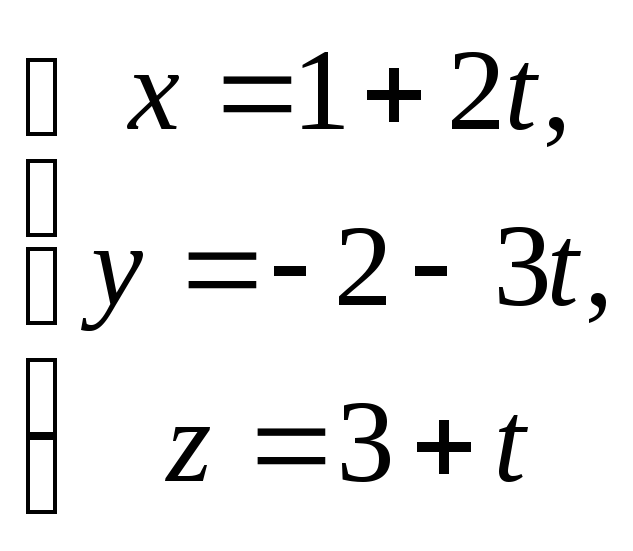и
.
Пример
13.
Составить параметрические уравнения
прямой, проходящей через точки
и
.
Решение.
Подставим координаты заданных точек в
уравнение прямой, проходящей через эти
точки:
или
.
Последние уравнения являются каноническими
уравнениями прямой, где
,
,
,
,
,
.
Подставим в параметрические уравнения
прямой и получим искомые уравнения:
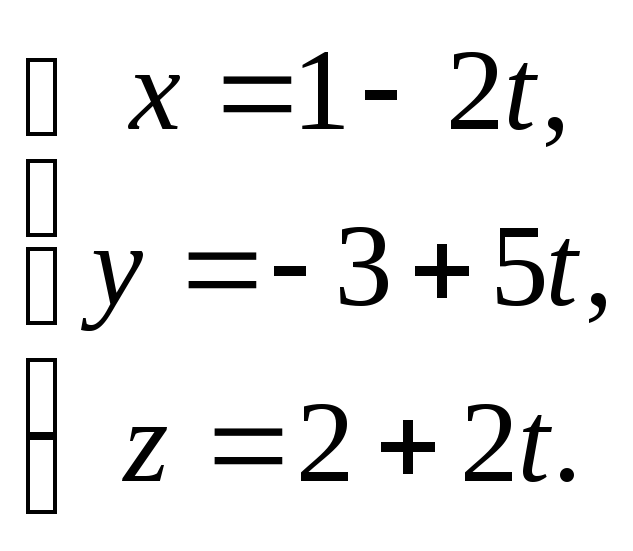
Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, нормальные векторы которых не коллинеарны:
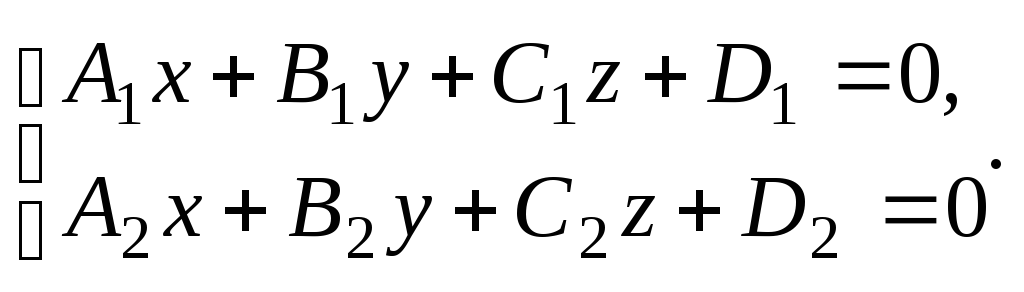
Пример
14.
Найти канонические уравнения прямой,
являющейся линией пересечения двух
плоскостей
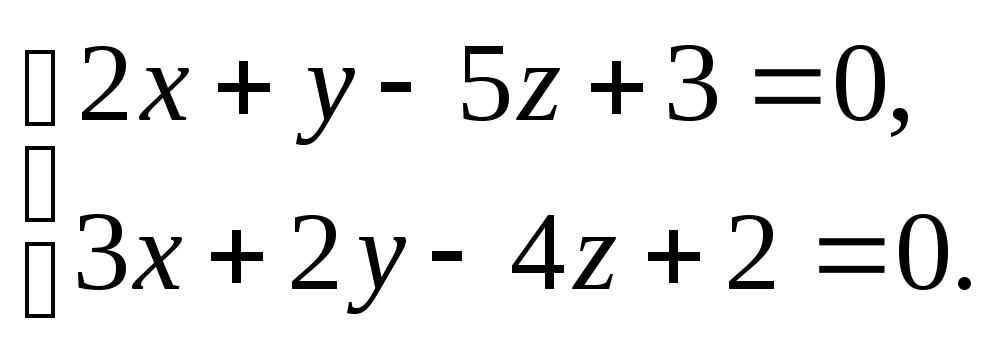
Решение.
Разрешим данную систему относительно
x
и y.
Первое уравнение умножим на (
2):
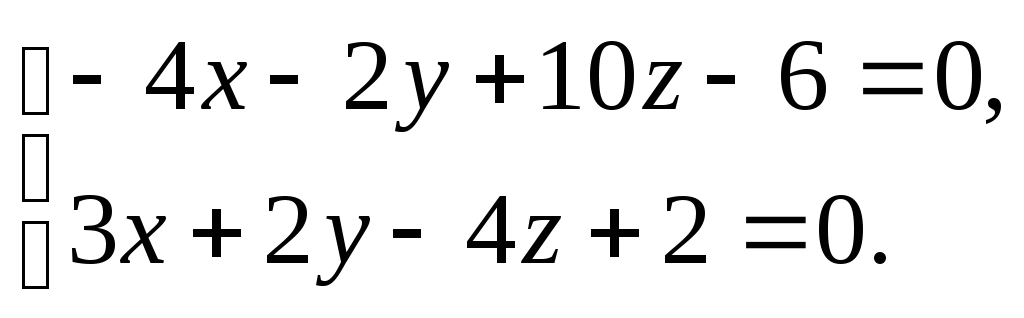Сложим со вторым и получим:
или
.
Подставим в первое уравнение:
или
.
Полученные равенства разрешим относительно
z:
и
. Тогда можно записать
.
Получены
канонические уравнения прямой, являющейся
линией пересечения двух данных плоскостей.
Пусть даны две прямые
и
,
где
и
- их направляющие векторы. Угол между
этими прямыми определяется по формуле
.
Прямые
параллельны, если их направляющие
векторы коллинеарны, т.е.
.
Эти соотношения являются условием
параллельности двух прямых.
Две
прямые взаимно перпендикулярны, если
их направляющие векторы
и
ортогональны. Следовательно, скалярное
произведение этих векторов равно нулю,
т.е.
.
Это
равенство выражает необходимое
и достаточное условие перпендикулярности
двух прямых.
Пример 15. Даны пары прямых:
а)
и
;
б)
и
;
в)
и
.
Определить, какие из этих пар прямых параллельны, а какие – взаимно перпендикулярны.
Решение.
а) Направляющие векторы прямых
и
.
Координаты векторов пропорциональны:
.
Так как условие параллельности прямых
выполняется, то прямые параллельны.
б)
Направляющими векторами прямых являются
и
.
Их скалярное произведение равно нулю:
.
В данном случае выполняется условие
перпендикулярности прямых, т.е. прямые
взаимно перпендикулярны.
в)
Координаты направляющих векторов
и
прямых не пропорциональны и скалярное
произведение этих векторов не равно
нулю, т.е. прямые не параллельны и не
перпендикулярны. Найдём угол между
прямыми, который равен углу между их
направляющими векторами:
.
Следовательно,
.